2022.09.07
Robust scaler
Introduction
난 평소에는 데이터 정규화를 위해 sci-kit learn 에서 제공하는 min-max scaler를 많이 사용한다. 그러나, 연구 중 outlier가 많은 데이터를 다루게 되었는데, min-max scaler를 사용하니 outlier를 제외한 나머지 값들이 매우 작은 수 (1e-4 정도)로 정규화 되는 문제가 있었다.
이를 해결하기 위해 "outlier, data normalization" 이라는 키워드로 구글링 해보니 robust scaler가 검색되었다. 빠르게 훑어보니 다른 정규화 방법에 비해 outlier에 강하기 때문에 안정적으로 정규화가 가능하다고 한다. 애초에 이름 자체가 robust scaler 이니 얼마나 안정적일까!
Robust scaler
robust sacler는 데이터의 Interquartile Range (IQR)을 사용한다. 데이터의 하위 25 % 값에 해당하는 Q1, 중간값에 해당하는 Q2, 상위 25 % 값에 해당하는 Q3를 통해 데이터를 정규화 하는데, 데이터 x에 대해 다음과 같이 나타낼 수 있다.
norm_x = (x - Q2) / (Q3 - Q1)
이는 중간 값 Q2를 기준으로 하여 50 % 의 데이터가 포함되는 Q1 ~ Q3 으로 데이터를 정규화한다는 의미이다. 이를 통해, 정규화의 기준이 Q1, Q3를 크게 벗어나는 outlier의 영향을 받지 않게 되는 것이다.
Is the Robust scaler robust?
처음 "robust scaler는 outlier로 부터 안정적이다." 라는 문구를 보고 sci-kit learn 라이브러리로 무작정 실험해보았을 때에는 robust scaler를 사용하면 정규화가 진행되면서 outlier들 역시 일정한 수준으로 (일반적인 값들과 비슷하게) 감쇄되리라고 기대했다. 그러나, 실험을 해보자 outlier들이 그대로 남아있었기에 당황했다. 왜 그런지 이해하기 위해 공식을 찾아보니 상술한 식과 같았다. robust scaler는 linear한 정규화 식을 사용하기에 outlier는 당연히 그대로 남아있는 것이다.
그렇다면 outlier를 제거하지 못하는 robust scaler가 무엇이 안정적이라는 걸까? 다음은 sci-kit learn에서 공식 문서[1] 에 나와 있는 실험이다.
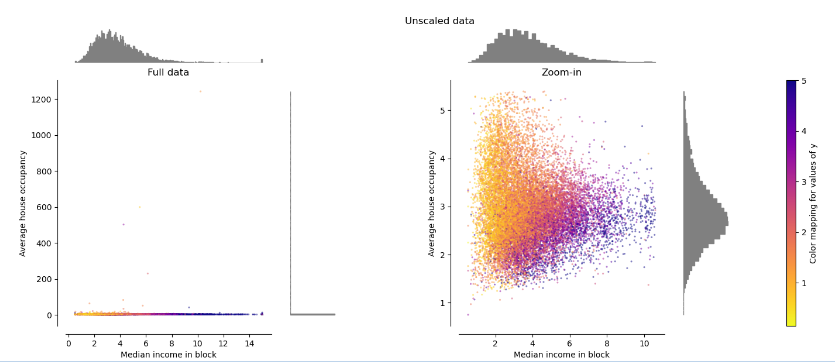
원본 데이터
실험에 사용한 데이터는 그림과 같이 x축은 중위소득, y축은 소유한 주택의 수이다. 그림의 왼쪽을 보면 일반적인 중위소득 구간 안에서 주택을 200 ~ 1200 가구나 보유하고 있는 사람들 즉, outlier가 있는 것을 볼 수 있다. (부동산 갭투자, 깡통 전세 뉴스가 매일 나오는 지금 다시보면 의미심장한 실험이다.) 그림의 오른쪽은 1~5 가구를 소유한 구간을 확대한 그림이다.
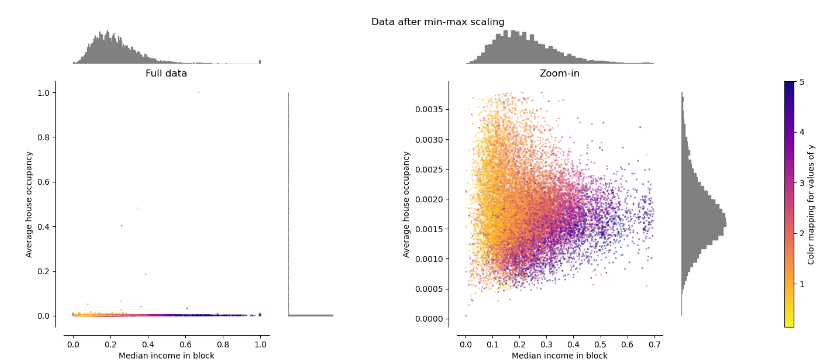
Min-max scaler로 정규화한 데이터
다음은 min-max scaler로 정규화한 데이터이다. 그림의 왼쪽을 보면 0.0 ~ 1.0 구간으로 정규화 되었지만, 그림의 오른쪽과 같이 outlier로 인해 일반적인 데이터들은 매우 작은 수로 정규화된 것을 알 수 있다.
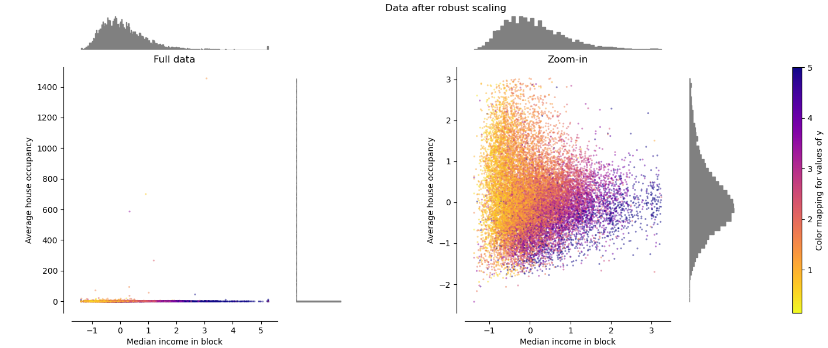
Robust scaler로 정규화한 데이터
다음은 robust scaler로 정규화한 데이터이다. 그림의 오른쪽을 보면, 데이터가 비교적 큰 수로 정규화 되면서도 min-max scaler로 정규화한 결과와 유사하게 정규화 되었다. robust scaler가 안정적이라 함은 정규화의 기준 자체가 안정적이라는 것이며 train set에 새로운 outlier가 추가되어도 정규화 기준이 바뀌지 않는다는 것이다. 왼쪽 그림과 같이, outlier를 제거할 것이라는 내 기대는 틀렸다.
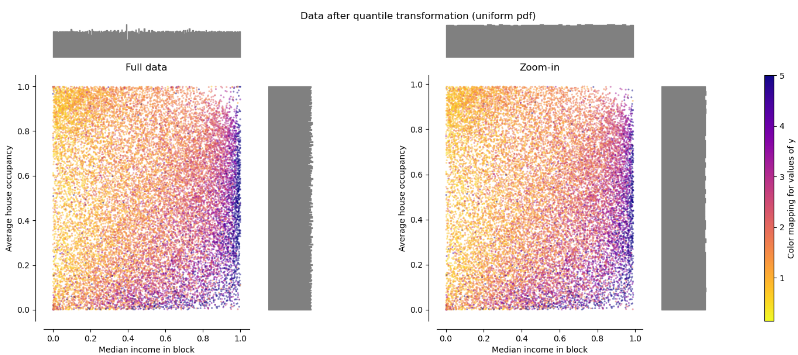
Quantile transformer로 정규화한 데이터
sci-kit learn에서는 non-linear한 scaler를 사용해서 그림과 같이 outlier를 없앨 수 있다고 말한다. 내가 생각한 방법과 유사하지만 과연 이게 내가 원하는 방식일까? 더 생각해봐야 할 문제이다.
Conclusion
robust scaler는 내 예상과 달리 outlier를 제거하거나 감쇄하는 기능이 있는 것이 아니라, outlier의 추가에도 정규화의 기준이 변하지 않는다는 의미에서 안정적인 정규화 방식이었다. non-linear한 정규화 방법을 사용해 내가 생각한대로 데이터를 정규화하면서 outlier를 자동으로 감쇄할 수 있다는 것을 알게 되었지만 이러한 방식들은 데이터의 원래 분포 자체를 크게 바꾸어 버린다. 이것이 정말 내가 원하는 (딥러닝 모델의 성능을 개선할 수 있는) 방식일지는 더 알아봐야 할 것이다.