Programmers | 더 맵게 - Python

1. 개념 정리

1.1 힙 (Heap)

최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진 트리를 기본으로 하는 자료구조이다. 힙은 최소 힙과 최대 힙으로 나누어지며, 키값의 대소관계는 오로지 부모 노드와 자식 노드간에만 성립한다. 형제 사이의 대소관계는 정해지지 않는다.

1. 최소 힙 : 부모 노드의 키 값이 자식 노드의 키값보다 항상 작은 힙
2. 최대 힙 : 부모 노드의 키 값이 자식 노드의 키값보다 항상 큰 힙

파이썬에서는 우선순위 큐를 구현하기 위해서 힙 관련 라이브러리를 사용한다. PriorityQue와 heapq가 있는데, 실행 시간 측면에서는 heapq가 더 좋고 스레드 안전성까지 고려한다면 PriorityQue를 사용하는 것이 좋다. (자세한 설명은 하단의 stack overflow 링크를 참조해주세요)

1.1.1 heapq()

이진 트리 기반의 최소 힙 자료 구조를 제공한다. (아래와 같은 조건에 맞춰 최소 힙을 구성한다.)

• 모듈 사용법과 관련한 Dale Seo님의 블로그 게시글을 참조해서 작성했습니다.

heap[k] <= heap[2*k+1] and heap[k] <= heap[2*k+2]

     1  ---> root
   /   \
  3     5
 / \   /
4   8 7

• 기본 사용 방법

import heapq

heap = [] # 최소 힙 생성

heapq.heappush(heap, 1) # 원소 추가 (힙 구조 유지)

print(heap[0]) # 삭제하지 않고 최솟값 얻기
heapq.heappop(heap) # 최솟값 삭제 (힙 구조 유지)

heap = [1, 2, 10, 5, 8]
heapq.heapify(heap) # 리스트 힙으로 변환

• 최대 힙 구성

heapq.heappush(heap, (-num, num)) # (우선순위, 값)

2. 문제 설명

2.1 더 맵게

매운 것을 좋아하는 Leo는 모든 음식의 스코빌 지수를 K 이상으로 만들고 싶습니다. 모든 음식의 스코빌 지수를 K 이상으로 만들기 위해 Leo는 스코빌 지수가 가장 낮은 두 개의 음식을 아래와 같이 특별한 방법으로 섞어 새로운 음식을 만듭니다.

섞은 음식의 스코빌 지수 = 가장 맵지 않은 음식의 스코빌 지수 + (두 번째로 맵지 않은 음식의 스코빌 지수 * 2)

Leo는 모든 음식의 스코빌 지수가 K 이상이 될 때까지 반복하여 섞습니다.
Leo가 가진 음식의 스코빌 지수를 담은 배열 scoville과 원하는 스코빌 지수 K가 주어질 때, 모든 음식의 스코빌 지수를 K 이상으로 만들기 위해 섞어야 하는 최소 횟수를 return 하도록 solution 함수를 작성해주세요.

2.2 제한 조건

• scoville의 길이는 2 이상 1,000,000 이하입니다.
• K는 0 이상 1,000,000,000 이하입니다.
• scoville의 원소는 각각 0 이상 1,000,000 이하입니다.
• 모든 음식의 스코빌 지수를 K 이상으로 만들 수 없는 경우에는 -1을 return 합니다.

2.3 입출력 예시

scoville	K	return
[1, 2, 3, 9, 10, 12]	7	2

3. 풀이 과정

모든 음식의 스코빌 지수를 확인해서 기준값 K 이하가 존재할 경우, 스코빌 지수를 K 이상으로 만들기 위한 최소 횟수를 구하는 문제이다. 우선순위 큐를 사용할 줄 안다면 쉽게 풀 수 있는 단순한 문제였다. 다만 파이썬에서는 우선순위 큐를 구현할 방법이 2가지가 있는데, 실행 시간까지 고려해서 적합한 방법을 사용해야 한다.

3.1 PriorityQue : 실패😂

알고리즘을 구성하는 것은 아주어렵지 않았는데 PriorityQue의 경우 실행 시간이 오래 걸려서 효율성 부분에서 실패하였다.

• 전체 코드 (Python)

from queue import PriorityQueue

def solution(scoville, K):
    # 스코빌 지수로 우선순위 큐를 구현
    queue = PriorityQueue()
    for sco in scoville:
        queue.put(sco)
    
    answer = 0
    # 모든 스코빌 지수가 K 이상이 되거나, 모든 음식이 합쳐질 때까지 반복 
    while True:  
        first = queue.get() # 가장 맵지 않은 음식의 스코빌 지수
        if queue.qsize() == 0: # 모든 음식이 합쳐졌을 경우
            return -1 if first < K else answer # K 이하면 -1 반환, 그렇지 않으면 answer 반환
        elif first < K: # 스코빌 지수가 K 이하인 음식이 있으면 공식에 따라 새 스코빌 지수 저장
            second = queue.get() 
            queue.put(first + second * 2)
            answer += 1 
        else: # 모든 음식의 스코빌 지수가 K 이상일 경우 answer 반환
            return answer

• 실행 결과
  

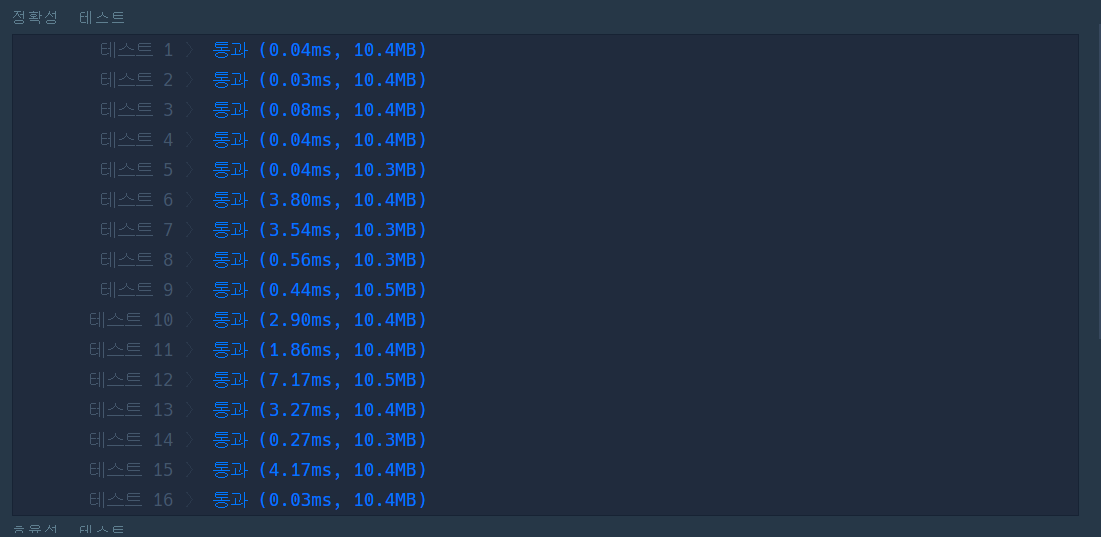
3.2 Heapq : 성공😋

위와 동일한 알고리즘이지만 시간 효율을 고려해서 heapq를 사용해서 풀이해보았다. PriorityQue와 비교했을 때 확연한 성능차이를 보이며 효율성 검사를 모두 통과할 수 있었다. 코딩 테스트 문제 풀이를 하는 경우는 실행 시간제한이 있기 때문에 우선순위 큐를 구현할 때 heapq방식으로 하는 것이 좋을 듯하다.

• 전체 코드 (Python)

import heapq

def solution(scoville, K):
    heapq.heapify(scoville)
    
    answer = 0
    while True:  
        first = heapq.heappop(scoville)
        if not scoville:
            return -1 if first < K else answer
        elif first < K:
            second = heapq.heappop(scoville)
            heapq.heappush(scoville, first + second * 2)
            answer += 1
        else:
            return answer

• 실행 결과
  

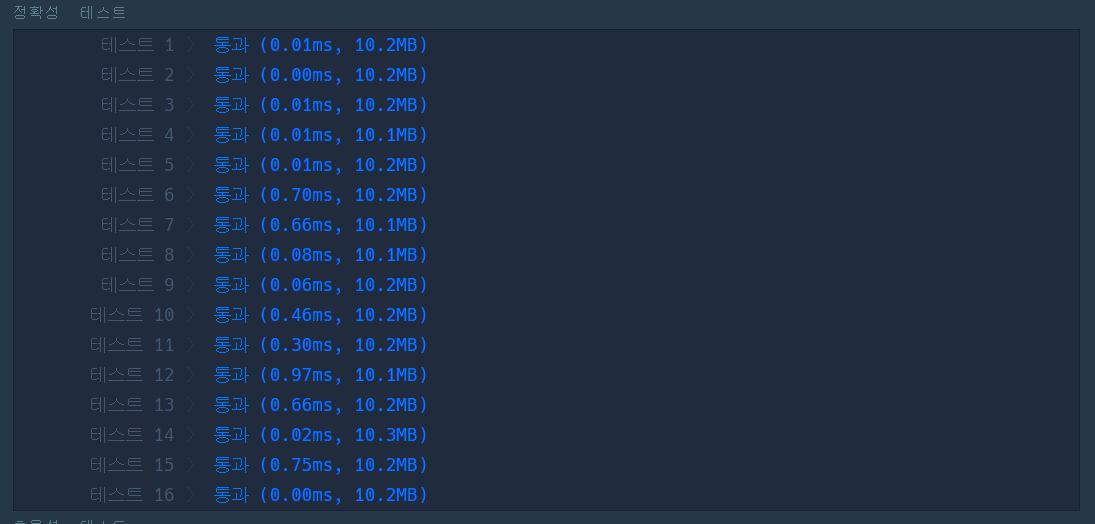
4. 핵심 정리

4.1 🔥 최종 풀이 🔥

import heapq

def solution(scoville, K):
    heapq.heapify(scoville)
    
    answer = 0
    while True:  
        first = heapq.heappop(scoville)
        if not scoville:
            return -1 if first < K else answer
        elif first < K:
            second = heapq.heappop(scoville)
            heapq.heappush(scoville, first + second * 2)
            answer += 1
        else:
            return answer

4.2 핵심 포인트

• 우선순위 큐를 구현하는 방식
• PriorityQue와 heapq의 성능 차이 인지하기
• max heap, min heap 구성 방식 익히기

4.3 주요 라이브러리

• PriorityQue

• heapq

4.4 참고 링크

• [위키백과] 힙(자료구조)
• [파이썬] heapq 모듈 사용법
• What's the difference between heapq and PriorityQueue in python?