[js] 에라토스테네스의 체 | 소수 판별 알고리즘

에라토스테네스의 체 원리

골드바흐 파티션 문제를 보다가 에라토스테네스의 체 알고리즘을 접하게 되었다.

소수 - 1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수

에라토스테네스의 체는 소수를 판별하는 알고리즘으로 1을 제외하고 2부터 N까지 자신을 제외하고 자신의 배수들을 지워하면서 소수들만 남기는 원리

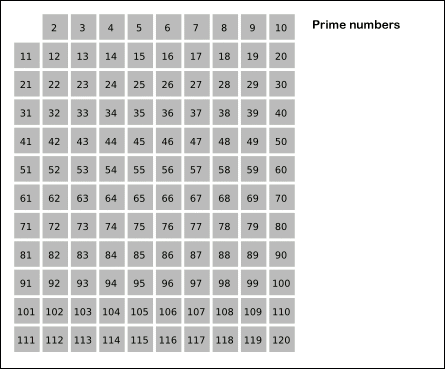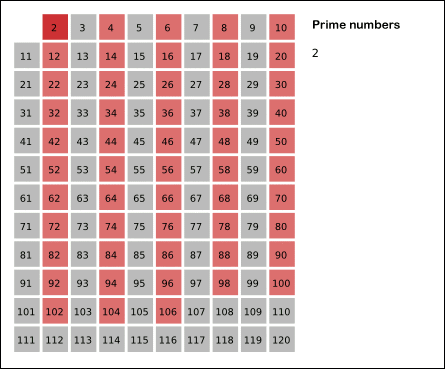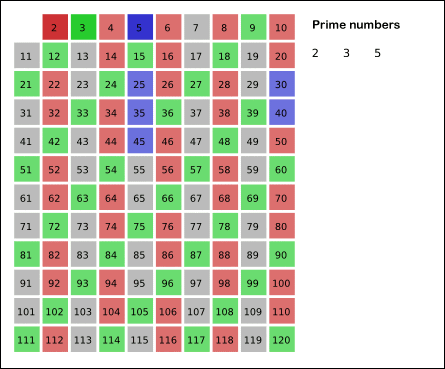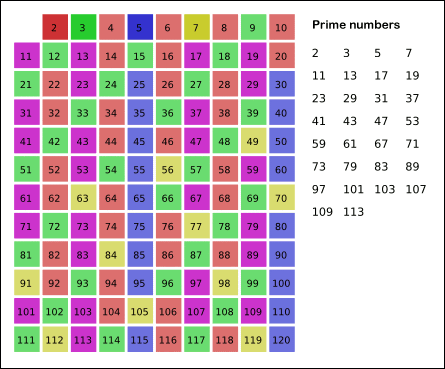
ex) N = 25 일 경우

1. 2부터 실행 ( 1은 소수가 아님)
2. 2을 제외한 2의 배수를 모두 제거

   2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

3. 2번에서 지우지 않은 수 들 중에 3을 제외한 3의 배수를 모두 제거

   2 3 5 7 9 11 13 15 17 19 21 23

4. 4는 삭제됨
5. 5의 배수 제거

   2 3 5 7 11 13 17 19 23

* √n까지만 검사해도 결과는 같음. √25 = 5

function prime_list(n){
    //에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
    let sieve = []
    for(let i = 2; i < n; i++){
      sieve.push(true);
    }

    //n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
    let m = parseInt(n ** 0.5, 10);
    for(let i = 2; i <= m; i++){
        if (sieve[i] == true){      // i가 소수인 경우 
          for(let j = i+i; j < n; j+=i){ // i이후 i의 배수들을 False 판정
                sieve[j] = false;
            } 
        }
    }

    // 소수 목록 산출
    let prime = [];
    for(let i = 2; i < n; i++){
      if (sieve[i] == true){
        prime.push(i);
      }
    }

    return prime;
}요

1. 가장 먼저 소수를 판별한 범위만큼 배열 할당
2. 제곱근 √n => n ** 0.5 or Math.sqrt(n)하여 검사
3. 배수들을 하나씩 삭제