Recursion
재귀란 자기 자신을 호출하여 해결하는 기법이다. 재귀에서의 가장 기본적인 원칙은 Divide and Conquer, 즉 순환이 일어날 때마다 문제의 크기는 줄어드는 것이다. factorial, 이항계수, 이진트리 알고리즘, 이진탐색, 하노이 탑을 구현하는데 유용한 방식이다.
구조
int facotrial(int n){
if(n<=1) return 1; //recursion을 멈추는 부분
else return n*factorial(n-1); //recursion을 호출하는 부분재귀는 1. 재귀를 멈추는 부분과 2. 재귀를 호출하는 부분 두 파트로 나누어져있다.
Recursion vs Iteration
대부분의 재귀는 반복의 형태로 구현되어있다. 재귀는 함수의 주소를 callback하는데 걸리는 overhead가 있기 때문에 대체로 실행속도가 느리다. 여기서 중요한 것은 이 느린 실행속도를 divide and conquer로 어떻게 줄이느냐 관건이다.
재귀는 항상 memory & call overhead가 iteration에 비해 크다. 함수를 불러오는 과정에서 생기는 overhead이기 때문이다. 재귀함수가 자기 자신을 호출할 때 스택 영역에 계속 누적이 된다. 대부분 stack 영역은 따로 설정하지 않으면 1MB등의 작은 크기로 설정이 되어있다. 때문에 재귀를 잘못 구현하면 stack overflow 문제에 직면할 수 있다.
대체로 iteration이 recursion보다 빠른데, factorial, 이항계수, 이진트리 알고리즘, 이진탐색, 하노이탑과 같은 문제에서는 recursion이 iteration보다 좋은 선택이 된다.
하지만 피보나치를 구현할 때 recursion은 추천하지 않는 방법인데, 왜인지 한번 살펴보자.
예를 들어, 재귀형식으로 구현된 피보나치가 있다고 해보자.
int fibo(int n){
if(n<=1) return 1;
return fibo(n-1)+fibo(n-2);
피보나치 수열은 정의 자체가 재귀로 되어있기 때문에 구현하기 어렵지 않다. 하지만 이렇게 됐을 때 어마어마한 시간복잡도에 직면할 수 있다.
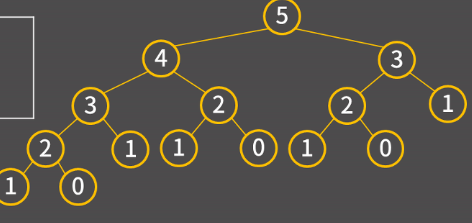
호출한 함수를 또 호출한다는 문제가 발생하기 때문이다. 또한 만약 fibo(n)이 호출되었을 경우, 시간복잡도가 2^n이 된다. 따라서 피보나치를 구현할 때는 iterator 방식으로 구현하는 것이 좋다.
연습문제 1 - 거듭제곱
int func(int a, int b, int m){
int val = 1;
while(b--) val *=a;
return val%m;
}func(6,100,5)를 넣으면 1이 아니라 0이 나온다 왜일까?
int형의 overflow 때문이다. 6을 100번 곱하면 int 자료형의 범위를 넘어가게 된다. 때문에 범위를 long long으로 바꾸고, 100번을 모두 곱한후 나머지를 구하는 것이 아니라 매번 곱할 때마다 나머지를 구하는 것이 메모리 측면에서 효율적이다.
