사전에 알아두어야 할 용어
- 순열: 요소 n개 중에 m개를 선택하여 순서에 상관 있게 뽑는 경우의 수
- 조합: 순서에 상관없이 요소 n개 중에 m개를 뽑는 경우의 수
- !(Factorial, 팩토리얼): n!은 n에서부터 1씩 감소하여 1까지의 모든 정수의 곱 (n보다 작거나 같은 모든 양의 정수의 곱). 팩토리얼에서 0!과 1!은 모두 1임.
문제: 카드 뽑기
A, B, C, D, E로 이루어진 5장의 카드. 이 5장의 카드 중 3장을 선택하여 나열하려고 할 때, 다음 조건을 각각 만족하는 경우를 찾아야 함.
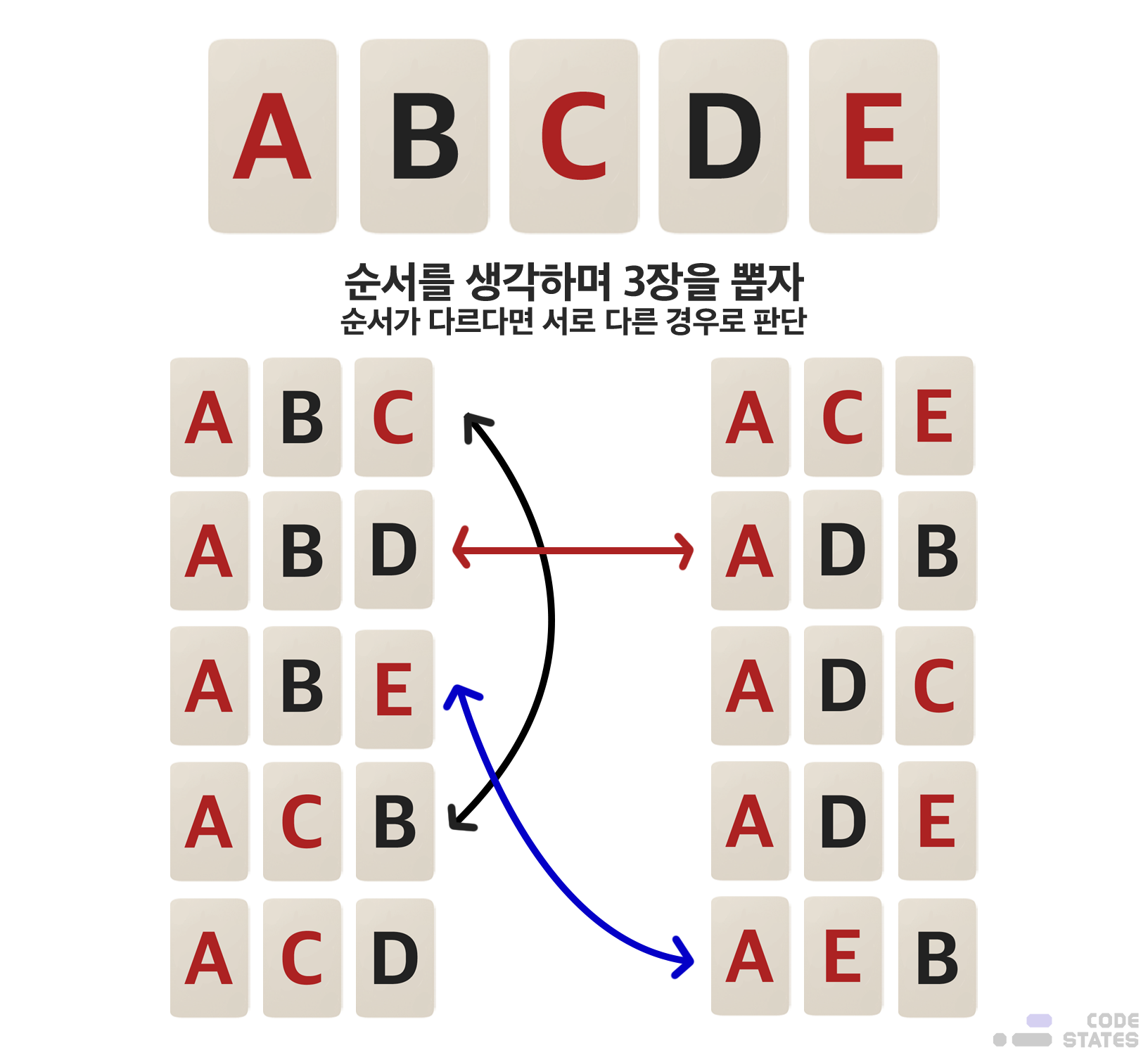
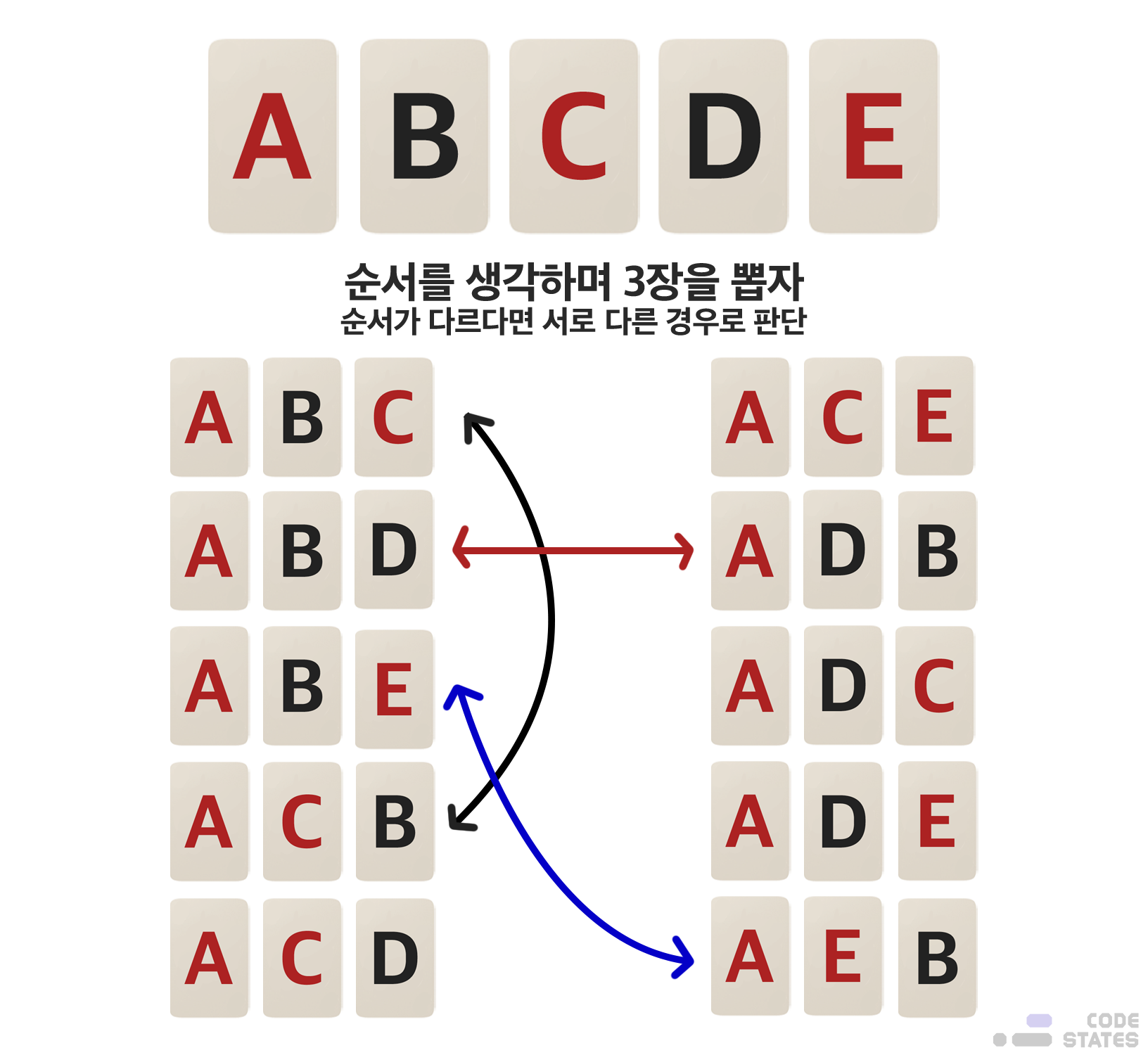
1. 순서를 생각하며 3장 선택하기
2. 순서를 생각하지 않고 3장 선택하기
case 1. 순서를 생각하며 3장을 선택할 때의 모든 경우의 수
모든 카드를 한 장씩 나열하면서 나열된 카드가 3장에 도달하면 카드의 나열을 중지함. 해당 조건을 만족하려면 다음과 같은 방법으로 경우의 수를 구함.
- 첫 번째 나열하는 카드를 선택하는 방법에는 다섯가지가 있음.
- 첫 번째 카드를 나열하고 난 다음, 두 번째 카드를 선택하는 방법에는 네 가지가 잇음
- 두 번째 카드를 나열하고 난 다음, 세 번째 카드를 선택하는 방법에는 세 가지가 있음
따라서 5X4X3=60 가지의 방법이 있음
이렇게 n개 중에서 일부만을 선택하여 나열하는 것을 순열이라고 함. 순열은 순서를 지키며 나열해야함.
예를 들어 가드를 3장 뽑을 때, [A,B,D]와 [A,D,B] 두 경우 모두 A, B 그리고 D라는 같은 가드를 3장 선택했지만, 나열하는 순서가 다르므로 서로 다른 경우로 파악해야함.
순열은 일반화 과정을 거쳐 Permutation의 약자 P로 표현함.
- 5장에서 3장을 선택하는 모든 순열의 수 = 5P3 = ( 5 X 4 X 3 X 2 X 1) / ( 2 X 1) = 60
- 일반식: nPr = n! / (n-r)!
- 5! = 5 X (5-1) X (5-2) X (5-3) X (5-4) = 5 X 4 X 3 X 2 X 1 = 120
// 반복문 코드
public static ArrayList<String[]> permutationLoop() {
// 순열 요소가 인자로 주어질 경우, 인자 그대로 사용하면 되지만, 인자가 주어지지 않고
// 문제 안에 포함되어 있을 경우 이런 식으로 직접 적어서 사용합니다.
String[] lookup = new String[]{"A", "B", "C", "D", "E"};
ArrayList<String[]> result = new ArrayList<>();
for (int i = 0; i < lookup.length; i++) {
for (int j = 0; j < lookup.length; j++) {
for (int k = 0; k < lookup.length; k++) {
if (i == j || j == k || k == i) continue;
String[] input = new String[]{lookup[i], lookup[j], lookup[k]};
result.add(input);
}
}
}
return result;
}result 배열 안에 순열의 경우의 수를 삽입한 뒤, 반환하는 함수
- 반복문의 개수 == 요소를 뽑는 개수
- 5개의 요소 중 3개를 뽑는 조건: 하나의 반복문당 5개의 요소(lookup.length)를 순화하고, 반복문을 3번 중첩하여 3개의 요소를 뽑음.
// 반복문 1개당 1개의 요소를 뽑습니다.
for (int i = 0; i < lookup.length; i++) {
String pick1 = lookup[i];
for (int j = 0; j < lookup.length; j++) {
String pick2 = lookup[j];
for (letintk = 0; k < lookup.length; k++) {
String pick3 = lookup[k];
if (i.equals(j) || j.equals(k) || k.equals(i)) continue;
result.add(new String[]{pick1, pick2, pick3});
}
}
}- 중복된 요소는 제거
- 같은 인덱스를 선택하는 것은 중복된 요소를 선택한다는 것과 같음. 하지만 순열은 중복된 요소를 허용하지 않기 때문에, result에 넣기 전에, 동일한 인덱스인지 검사하고 동일하다면 삽입하지 않고 다음으로 넘어감
- 'AAA'부터 'EEE'까지 전부 만드는 코드지만, 마지막에 중복 요소를 제거함으로써 순열이 완성됨
결과
/*
[
[ 'A', 'B', 'C' ], [ 'A', 'B', 'D' ], [ 'A', 'B', 'E' ],
[ 'A', 'C', 'B' ], [ 'A', 'C', 'D' ], [ 'A', 'C', 'E' ],
[ 'A', 'D', 'B' ], [ 'A', 'D', 'C' ], [ 'A', 'D', 'E' ],
[ 'A', 'E', 'B' ], [ 'A', 'E', 'C' ], [ 'A', 'E', 'D' ],
[ 'B', 'A', 'C' ], [ 'B', 'A', 'D' ], [ 'B', 'A', 'E' ],
[ 'B', 'C', 'A' ], [ 'B', 'C', 'D' ], [ 'B', 'C', 'E' ],
[ 'B', 'D', 'A' ], [ 'B', 'D', 'C' ], [ 'B', 'D', 'E' ],
[ 'B', 'E', 'A' ], [ 'B', 'E', 'C' ], [ 'B', 'E', 'D' ],
[ 'C', 'A', 'B' ], [ 'C', 'A', 'D' ], [ 'C', 'A', 'E' ],
[ 'C', 'B', 'A' ], [ 'C', 'B', 'D' ], [ 'C', 'B', 'E' ],
[ 'C', 'D', 'A' ], [ 'C', 'D', 'B' ], [ 'C', 'D', 'E' ],
[ 'C', 'E', 'A' ], [ 'C', 'E', 'B' ], [ 'C', 'E', 'D' ],
[ 'D', 'A', 'B' ], [ 'D', 'A', 'C' ], [ 'D', 'A', 'E' ],
[ 'D', 'B', 'A' ], [ 'D', 'B', 'C' ], [ 'D', 'B', 'E' ],
[ 'D', 'C', 'A' ], [ 'D', 'C', 'B' ], [ 'D', 'C', 'E' ],
[ 'D', 'E', 'A' ], [ 'D', 'E', 'B' ], [ 'D', 'E', 'C' ],
[ 'E', 'A', 'B' ], [ 'E', 'A', 'C' ], [ 'E', 'A', 'D' ],
[ 'E', 'B', 'A' ], [ 'E', 'B', 'C' ], [ 'E', 'B', 'D' ],
[ 'E', 'C', 'A' ], [ 'E', 'C', 'B' ], [ 'E', 'C', 'D' ],
[ 'E', 'D', 'A' ], [ 'E', 'D', 'B' ], [ 'E', 'D', 'C' ]
]
*/case 2. 순서를 생각하지 않고 3장을 선택할 때의 모든 경우의 수
2번 조건에서 모든 경우의 수를 구할 때는 3장을 하나의 그룹으로 선택해야 함
- 순열로 구할 수 있는 경우를 찾음
- 순열로 구할 수 있는 경우에서 중복된 경우의 수를 나눔
먼저 조합은 순열과 달리 순서를 고려하지 않음. 만약 순열처럼 순서를 생각하여 경우의 수를 센다면, 조합으로써 올바르지 않음. 예를 들어 순열에서는 [A, B, C], [A, C, B], [B, A, C], [B, C, A], [C, A, B], [C, B, A]의 여섯가지는 모두 다른 경우로 취급하지만, 조합에서는 이 여섯 가지를 하나의 경우로 취급함. 다시 말해 순열에서처럼 순서를 생각하여 선택하면, 중복된 경우가 6배 발생함.
여기서 나온 여섯 가지 경우의 수는 3장의 카드를 순서를 생각하여 나열한 모든 경우의 수임.
3장의 카드를 순열 공식에 적용한 결과가 3!/(3-3)! = (3X2X1) / 1 = 6 임. 순서를 생각하느라 중복된 부분이 발생한 순열의 모든 가지수를, 중복된 6가지로 나누어 주면 조합의 모든 경우의 수를 얻을 수 있음.
따라서 (5X4X3X2X1) / ((3X2X1) X (2X1)) = 10 임.
조합을 일반화 과정을 가쳐, Combination의 약자 C로 표현함.
- 5장에서 3장을 무작위로 섲택하는 조합에서 모든 경우의 수 = 5C3 = 5! / (3! * 2!) = 10
- 일반식: nCr = n! / (r! * (n - r)!)
조합의 모든 경우의 수
// 반복문 코드
public static ArrayList<String[]> combinationLoop() {
// 조합 요소가 인자로 주어질 경우, 인자 그대로 사용하면 되지만, 인자가 주어지지 않고
// 문제 안에 포함되어 있을 경우 이런 식으로 직접 적어서 사용합니다.
String[] lookup = new String[]{"A", "B", "C", "D", "E"};
ArrayList<String[]> result = new ArrayList<>();
for(int i = 0; i < lookup.length; i++) {
for(int j = i + 1; j < lookup.length; j++) {
for(int k = j + 1; k < lookup.length; k++) {
String[] input = new String[]{lookup[i], lookup[j], lookup[k]};
result.add(input);
}
}
}
return result;
}순열과 마찬가지로 result 배열 안에 순열의 경우의 수를 삽입한 뒤, 반환하는 함수
- 순열과 다른 점은, 반복의 조건에 있음 (i = 0, j = i + 1, k = j + 1)
- 한 번 조합한 요소는 다시 조합하지 않음. 하나의 요소로 만들 수 있는 모든 경우의 수를 다 구한 다음, 그 요소를 반복에 포함하지 않고 다음 요소부터 시작함
결과
/*
[
[ 'A', 'B', 'C' ], [ 'A', 'B', 'D' ], [ 'A', 'B', 'E' ],
[ 'A', 'C', 'D' ], [ 'A', 'C', 'E' ], [ 'A', 'D', 'E' ],
[ 'B', 'C', 'D' ], [ 'B', 'C', 'E' ], [ 'B', 'D', 'E' ],
[ 'C', 'D', 'E' ]
]
*/한계점
- 개수가 늘어나면 반복문의 수도 늘어남
- 만약, 11개의 요수 중 10개를 뽑아야 한다면, 10중 반복문을 구현해야 함. 이는 비효율적이고 보기 좋은(쉬운) 코드에 부합하지도 않음 - 뽑아야 되는 개수가 n개처럼 변수로 들어왔을 때 대응이 어려움
- 요소 개수를 변수로 받는 건요소.length를 사용하여 대응할 수 있지만, 뽑아야 되는 개수도 변수로 받게 된다면 몇 개의 반복문을 설정해야하는지, 설정은 어떻게 하는지 굉장히 까다로워짐