Deque
Deque의 정의
- Double ended Queue의 양방향 대기열이라고도 불리는 자료구조
- 예. 실의 양쪽에 구슬을 꿰어 넣는 것과 비슷한 구조
Deque의 구조
- Stack은 먼저 들어간 데이터가 먼저 나오는 LIFO(Last In First Out)의 특성을 가짐
- Stack의 구조는 데이터가 한 방향으로 데이터가 추가되고 삭제하는 형태로 한 방향으로만 열려있음. 먼저 저장된 데이터일수록 나중에 꺼낼 수 있고 나중에 들어간 데이터일수록 먼저 꺼낼 수 있음 - Queue는 나중에 들어간 자료가 먼저 나오는 FIFO(First In First Out)의 특성을 가짐
- Queue의 구조로는 데이터가 한 방향으로 데이터가 추가되고 다른 방향으로 데이터가 삭제되는 형태로 두 방향이 열려있음. 먼저 들어간 데이터일수록 먼저 꺼낼 수 있고 나중에 들어간 데이터일수록 나중에 꺼낼 수 있음
-> Deque는 이런 특성이 혼합되어 있음.
양방향으로 열려있는 구조로, queue와 외형적으로 비슷한 구조이나 한 방향인 queue와 다름. queue나 stack과 달리 LIFO나 FIFO와 같은 순서에 구속되지 않음.
Deque의 특징
- Stack 및 Queue를 모두 사용할 수 있음
Deque는 양쪽으로 데이터를 추가하고 삭제할 수 있어서 stack과 queue를 구현할 수 있음.추가와 삭제를 양쪽에서 제어할 수 있어서 여러가지 형태로 사용됨.
- 추가를 제한하는 구조
---------------------------
-> insert
<- delete delete ->
---------------------------데이터 추가의 방향이 정해진 상태가 됨. 왼쪽으로 삭제하는 형태는 stack과 같고 오른쪽으로 삭제하는 형태는 queue와 같음.
- 삭제를 제한하는 구조
데이터의 추가는 양쪽에서 가능하지만, 삭제는 한 방향에서만 가능하게 구현한다면 아래와 같은 구조가 됨.
---------------------------
-> insert insert <-
<- delete
---------------------------데이터 삭제의 방향이 정해진 상태가 됨. 이때 왼쪽에서 추가하는 형태는 stack과 같고 오른쪽에서 추가하는 형태는 queue와 같음.
두 예와 같이 양방향의 추가 또는 삭제를 제한하여 상황에 맞는 자료구조를 구현할 수 있음.
- 양방향 끝에서 데이터 추가, 삭제가 용이함
-----
3 // 3추가
-----
L R
-----------
2 | 3 // 왼쪽에 2추가
-----------
L R
-----------------
2 | 3 | 4 // 오른쪽에 4추가
-----------------
L R
-----------------------
1 | 2 | 3 | 4 // 왼쪽에 1추가
-----------------------
L RStack과 Queue에서 추가할 데이터나 삭제할 데이터의 인덱스 정보를 가지고 있듯이 Deque도 양쪽의 추가 삭제할 데이터의 인덱스 정보를 가지고 있어서 양쪽 끝의 데이터에 접근과 추가, 삭제가 용이함
- 양방향 끝이 아닌 임의이ㅡ 데이터만 추가하거나 삭제하는건 불간으함
Deque는 양방향 끝의 인덱스 정보를 가지고 있음. 앙방향의 데이터가 아닌 중간에 있는 데이터에 접근하려고 할 때 양쪽 끝 이외의 인덱스 정보가 없어서 접근할 수 없음. 이러한 구조로 deque는 임의의 인덱스만 추가 삭제하는 것은 불가능함.
Linked List
Linked List의 정의
Linked List 자료구조는 선형으로 그룹화된 데이터의 집합으로 데이터와 다음 데이터의 주소를 포함하고 있는 하나의 노드가 선형으로 연결된 자료구조임. 한글로는 연결 리스트라고도 함.
예. 배열(Array)은 교실에 있는 반 학생들이 일렬로 놓여있는 의자에 번호순으로 앉혀 놓은 상태임. 의자의 위치만으로도 빠르게 학생을 찾을 수 있음. Linked List 자료구조는 반 전체 학생 이름이 적힌 종이로 제비를 뽑아 마니또를 정한 상태와 같음. 첫 번째 학생부터 마지막 학생까지 마니또를 알기 위해서는 다음 마니또가 누구인지 한명 한명 물어보고 알아내야 함. 학생은 제비에 적힌 자신의 마니또밖에 모르기 때문임.
Linked List의 구조
Linked List는 배열과 같이 선형으로 이루어진 자료구조임. 배열과 비교하면 쉽게 이해할 수 있음.
- 배열(Array)은 연속된 공간 안에 메모리를 차지하고 인덱스로 각각의 요소의 데이터를 읽거나 쓸 수 있는 자료구조임. 연속된 메모리 주소값 안에 데이터를 넣는 구조로 위치를 바꾸려면 데이터가 이동해야 함.
- Linked list 자료구조는 연속된 공간이 아니라 흩어져 있는 공간에 노드들의 연결로 이루어진 자료구조임. 하나의 노드에는 데이터와 당므 노드의 주소가 담겨있음. 그리고 각 노드는 다음 노드를 가리킴. 연속된 메모리 주소가 아니기 때문에 직접 주소값을 가지고 있어야 다음 노드로 접근할 수 있음. 마지막 노드는 다음을 가리킬 곳이 없으므로 새로 추가되기 전까지는 null을 가리킴.
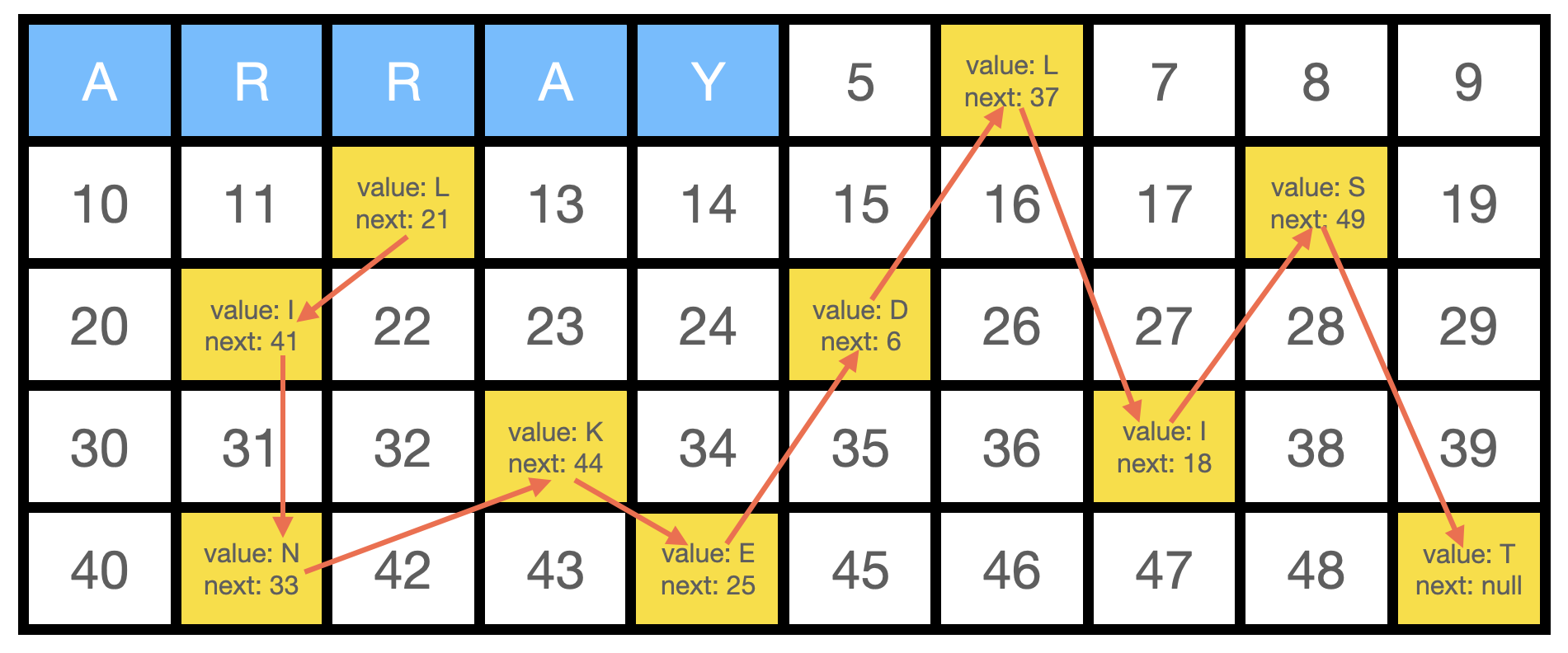
메모리에 표시한 링크드 리스트와 배열
Linked List의 특징
- 노드의 추가와 삭제가 빠르고 쉬움.
배열은 메모리 순서가 정해져 있어서 값을 추가하거나 삭제할 때 메모리에 재할당을 해야 하지만 Linked List는 순서가 지정되지 않은 특성 때문에 데이터를 담은 노드를 어디에도 손쉽게 추가하거나 삭제할 수 있음.
배열은 추가하거나 삭제하는 경우 때에 따라 시간 복잡도가 많이 걸림.
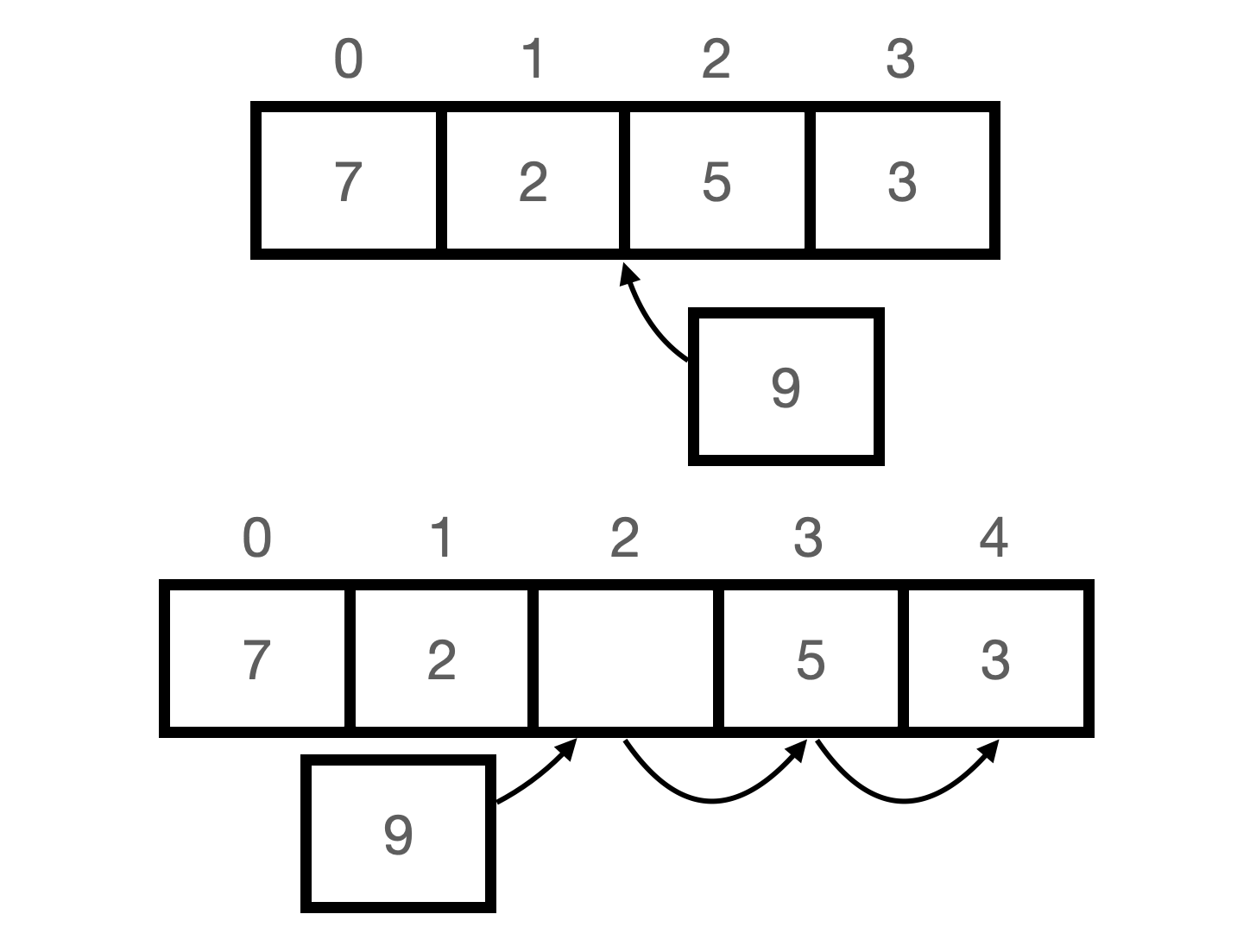
배열은 중간에 데이터를 추가하고 싶을 때 제일 마지막 인덱스를 새로 만들어서 삽입하고자 하는 인덱스까지 모든 데이터를 한 칸씩 이동한 다음에 원하는 인덱스의 값을 추가할 수 있음. 가장 마지막 인덱스에 데이터를 추가할 때 가장 O(1)의 빠른 시간 복잡도를 보이지만 -번 인덱스에 데이터를 추가하는 경우 모든 데이터를 오른쪽으로 옮겨야 하므로 최악의 경우 O(n)의 시간 복잡도를 가짐.
삭제는 추가의 반대 과정으로 동작함. 배열은 마지막 요소의 수정으 ㄴ빠르나 가장 앞의 요소 수정은 가장 오래 걸리게 됨.
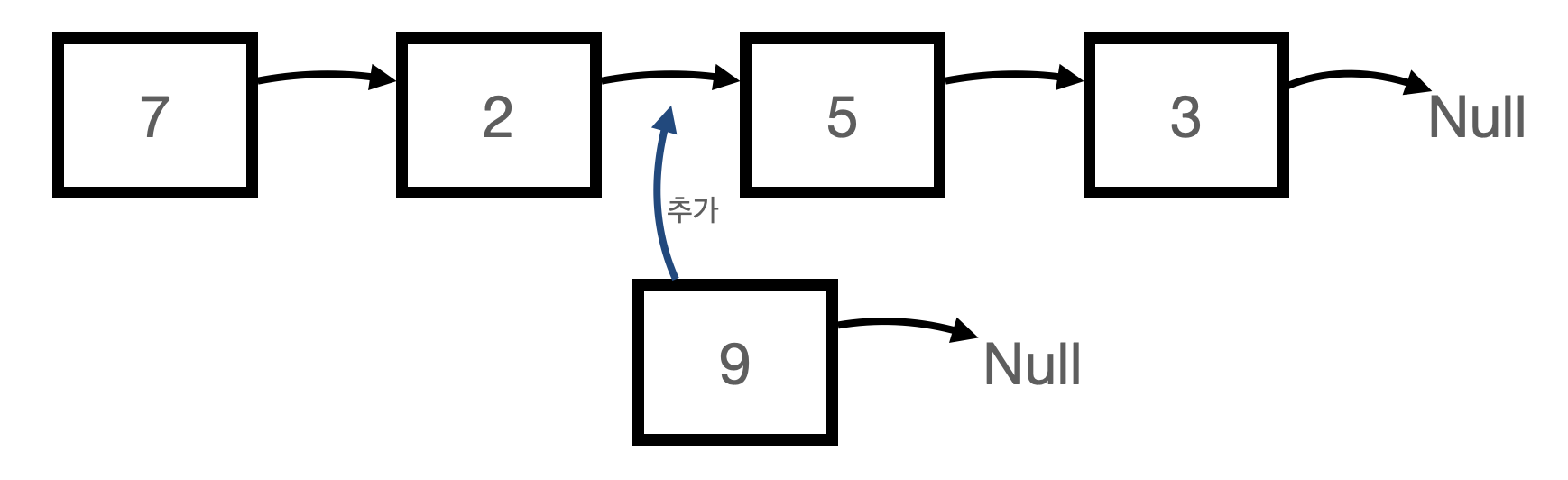
Linked List의 노드에는 데이터와 다음 노드의 메모리 주소가 함께 들어가 있음.
위 그림의 Linked List에서 데이터 추가해보기.
1. 7 → 2 → 5 → 3 으로 연결되어있음.
2. 7은 2를 가리키고, 2는 5를 가리키고, 3은 마지막에 있어서 아무것도 가리키고 있지 않음.
3. 이 상태에서 2와 5 사이에 9를 추가하려고 함. 여기서 추가하는 방법은 2는 9를 가리키게 바꾸고 9는 5를 가리키게 바꾸면 7 → 2 → 9 → 5 → 3 으로 Linked List에 9를 추가할 수 있음.
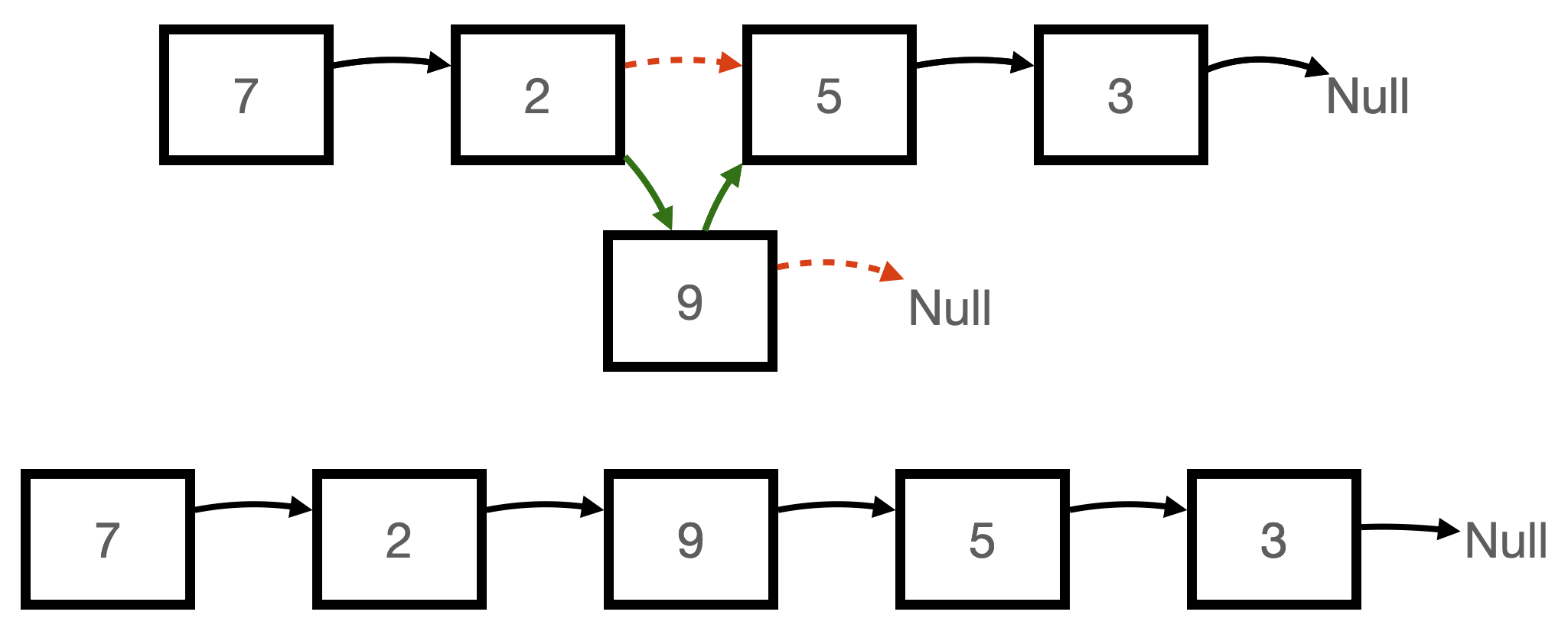
위 그림의 Linked List에서 데이터 삭제해보기.
1. 9를 삭제하려고 함.
2. 9는 5를 가리키고 있지만, 5를 가리키지 않고 null을 가리키게 바꿈.
3. 2는 9를 가리키고 있지만, 9를 가리키지 않고 5를 가리키게 바꿈.
4. 그렇게 되면 7 → 2 → 5 → 3으로 9를 Linked List에서 삭제할 수 있음. 삭제도 다음 노드를 가리키는 메모리 주소만 수정하면 됨.
이렇게 Linked List는 어떤 위치에 노드를 추가하거나 삭제해도 O(1)의 빠른 시간 복잡도를 보여줌.
- 노드의 값을 찾으려면 최대 전체를 순회해야 함.
배열과 비교해보자면, 배열은 연속적으로 이어져 있어 주소의 계산이 쉬워서 쉽게 접근할 수 있음. 하지만 Linked List의 노드는 메모리에 흩어져 있어서 특정 노드로 쉽게 접근할 수 없음.
- Array
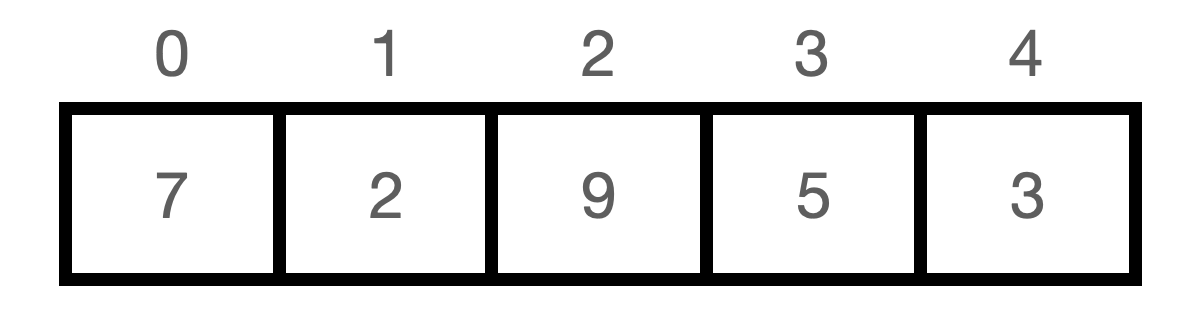
이런 식으로 배열은 물리적 메모리에 연속적으로 할당되어 있어서 주소에 접근하는것이 쉬움. 다음 메모리 주소에도 배열의 값이 있을 것이기 때문. 배열은 인덱스값을 계산하기가 쉬우므로 어느 위치의 인덱스인지 관계없이 데이터에 접근하는데 O(1)의 시간복잡도를 가짐.
- Linked List
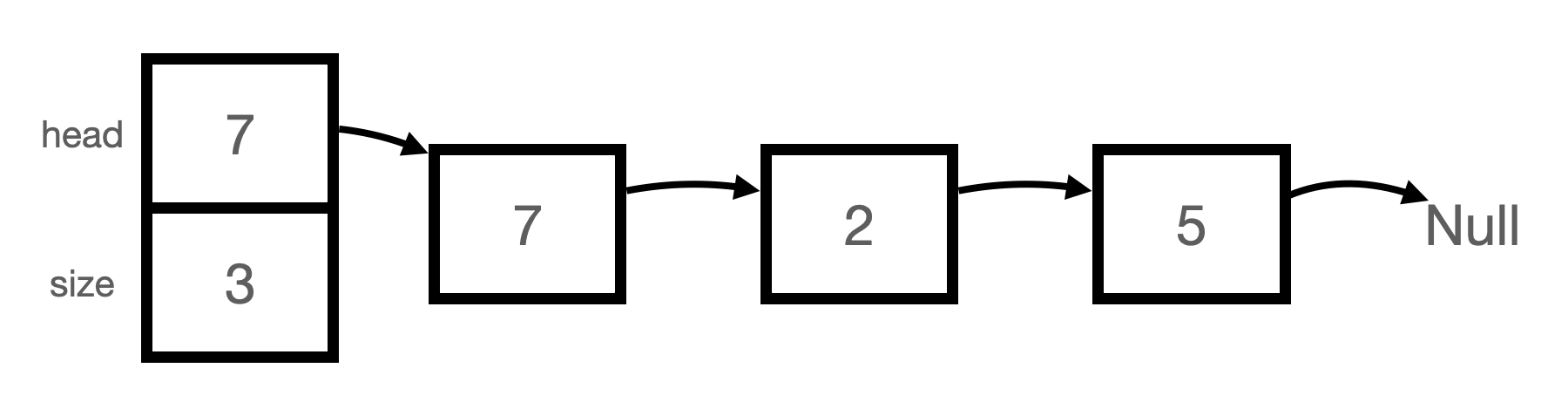
Linked List의 첫 번째 노드를 head node라고 함. 순회하기 전까지는 head node의 정보만 알고 있음. 필요한 값이 있는지 확인하려면 head node에 연결된 다음 노드로 접근해야 하고, 접근한 노드에 원하는 값이 없다면 다시 다음 노드로 이동해야 함. Linked List의 구조가 위와 같이 보이지만, 실제로는 아래 같은 정보가 주어져 있음.
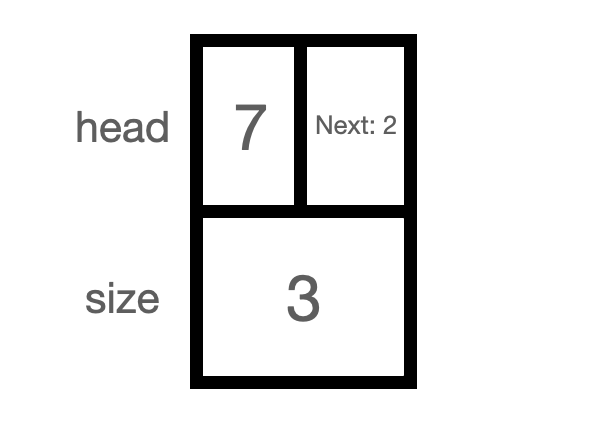
head node의 값은 7이고 뒤로 붙은 노드의 개수가 3개인 리스트를 말할 뿐, 그 뒤의 요소 정보를 전혀 알 수 없음. 3개의 요소 중 마지막 요소에는 무엇이 있는지 확인하려면 head node에서 출발하여 마지막 노드까지 전부 순회해야 5라는 것을 알게 됨. head node에 있는 값은 O(1)의 시간 복잡도를 가지지만 마지막 요소의 값에 접근하기 위해서는 요소의 개수만큼 순회해야 하기 때문에 최악의 경우로 O(n)의 시간복잡도를 가짐.
Linked List 실사용 예제
- 삽입과 삭제가 중요한 곳에 활용됨
- join, split method처럼 데이터 삽입 삭제가 중요한 메소드의 구현에도 활용할 수 있음 - 동적 기억장소 관리(dynamic storage management)
- 실행되는 작업에 필요한 크기만큼의 메모리를 할당하는 방법에 활용됨 - Garbage collection
- 참조자료형의 데이터 타입을 관리하는 알고리즘 중 하나
Hash Table
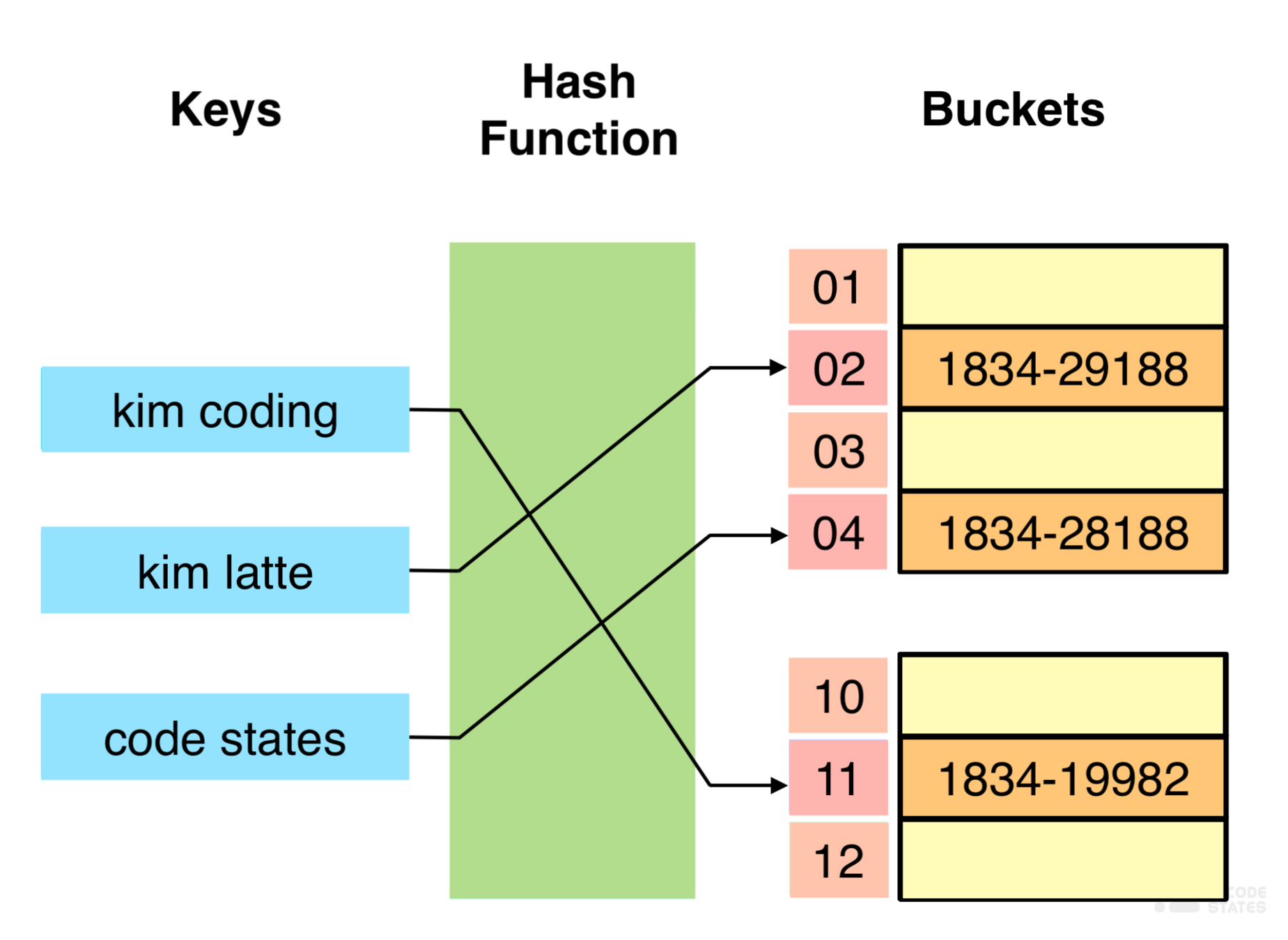
hash table이란 해시함수(hash function)를 사용하여 변환한 해시(hash)를 색인(index)으로 삼아 키(key)와 데이터(value)를 저장하는 자료구조.
예. 핸드폰 단축번호 설정
김코딩, 010-1234-5678, 단축번호:1 이라는 사람에게 전화를 걸기 위해 미리 사용자가 저장한 단축번호: 1을 누르면 010-1234-5678 번호로 바로 통화할 수 있음.
이처럼 필요한 키(key)를 해시함수를 사용해 별도의 해시(hash)로 바꿔주고, 해당하는 데이터(value)를 함께 저장하는 자료구조.
Hash Table의 구조
- 키(key): 고유한 값으로 해시 함수의 입력값이 됨. 다양한 길이의 값이 들어올 수 있음. 해시 함수를 통해 변환하지 않은 상태로 저장소에 저장이 되면 다양한 길이만큼의 저장소를 구성해두어야 하기 때문에 해시 함수로 값을 바꾸어 저장하게 됨.
- 해시함수(hash Function): 키(key)를 해시(hash)로 바꿔주는 역할을 함. 다양한 길이를 가지고 있는 키(key)를 일정한 길이를 가지는 해시(hash)로 변경하여 저장소를 효율적으로 운영할 수 있도록 도와줌. 다만 서로 다른 키(key)가 같은 해시(hash)가 되는 경우를 해시 충돌(hash collision)이라고 하는데 해시 충돌을 일으키는 확률을 최대한 줄이는 것이 중요함.
- 해시(hash): 키(key)를 해시함수(hash function)를 사용하여 만들어진 결과물로, 저장소에 데이터(value)와 매칭되어 저장됨. 변환된 값을 배열의 색인(index)고 같이 사용하게 됨.
- 데이터(value): 저장소에 최종적으로 저장되는 값으로 색인(index)과 매칭되어 저장됨.
Hash Table의 특징
hash table에서 저장, 삭제, 검색 과정은 모두 평균적으로 O(1)의 시간복잡도를 가지고 있어 데이터를 다루는 작업이 매우 빠르다는 장점이 있음. 다만 해시 충돌이 발생할 수가 있고 데이터가 저장되기 전에 저장공간을 미리 만들어놔야하기 때문에 공간 효율성이 떨어짐. 또한 해시 함수(hash function)의 의존도가 높음. 이 말은 곧, 해시 함수(hash function)가 복잡하다면, 해시(hash)값을 만들어내는데 많은 시간이 소요됨.
- 저장, 삭제, 검색 과정
hash table에서 저장, 삭제, 검색하기 위해서는 해시 함수(hash function)에 키(key)값을 넣어 해시(hash)값을 만들게 됨. 이후 만ㄷ르어진 해시(hash)값과 이맃하는 색인(index)을 찾아 저장하거나 삭제, 검색함.
기본적으로 해당 작업들의 시간 복잡도는 O(1)임.
해시함수(hash function)를 거쳐 해시값을 찾아내는데 걸리는 과정은 고려하지 않음. 그러나 해시충돌이 발생할 경우 저장소의 모든 색인(삽입) 혹은 데이터(삭제, 검색)를 찾아봐야 하기 때문에 O(n)이 됨.
- 대표적인 해시 알고리즘
- Division Method: Number type의 키를 저자소의 크기로 나누어 나온 나머지를 색인으로 사용하는 방법. 이때 저장소의 크기를 소수(prime number)로 정하고 2의 제곱수와 먼 값을 사용하는 것이 효과가 좋음. 예를 들어 key 값이 23일 때 테이블 크기가 7이라면 index는 2가 됨.
- Digit Folding: 키의 문자열을 ASCII 코드로 바꾸고 그 값을 합해 저장소에서 색인으로 사용하는 방법. 만약 이때 색인이 저장소의 크기를 넘어간다면
Division Method를 적용할 수 있음. - Multiplication Method: 숫자로 된 키 값 K와 01과 1 사이의 실수 A, 보통 2의 제곱수인 m을 사용하여 다음과 같이 계산한 값을 사용함. index = (KA mod 1)m
- Universal Hashing: 다수의 해시함수를 만들어 특정한 장소에 넣어두고, 무작위로 해시함수를 선택해 해시값을 만드는 기법
해시 충돌을 해결할 수 있는 방법
- 개방 연결법(Open Addressing)
개방 연결법이란 해시 충돌이 발생하면 다른 색인에 해당 자료를 삽입하는 방식. 여러 가지 방법이 존재하지만 대표적으로 3가지가 존재함.
- Linear probing: 현재 중복된 색인으로부터 고정된 숫자만큼 이동하여 비어있는 저장소(버킷)를 찾아 데이터를 저장함.
- Quadratic probing: 현재 중복된 색인으로부터 이동할 숫자를 제곱으로 사용하는 방식. 처음 충돌이 발생하면 1(1^2)만큼 이동하고, 또 충돌이 발생한다면, 4(2^2)만큼, 3번째는 9(3^2)만ㄴ큼, 4번째는 16(4^2)만큼 이동하여 빈 공간을 탐색하는 방법
- Double Hashing Probing: 하나의 해시함수에서 충돌이 발생한다면 미리 지정해둔 다른 해시함수를 이용해 새로운 주소를 받아 사용하는 방법. 다른 방법들보다 많은 연산이 필요하게 됨.
- 분리 연결법(Separate Chaining)
분리 연결법이란 동일한 색인의 데이터에 대해 연결리스트(linked list), 트리(red-black tree)등의 자료구조를 활용해 데이터의 주소를 저장하는 방법
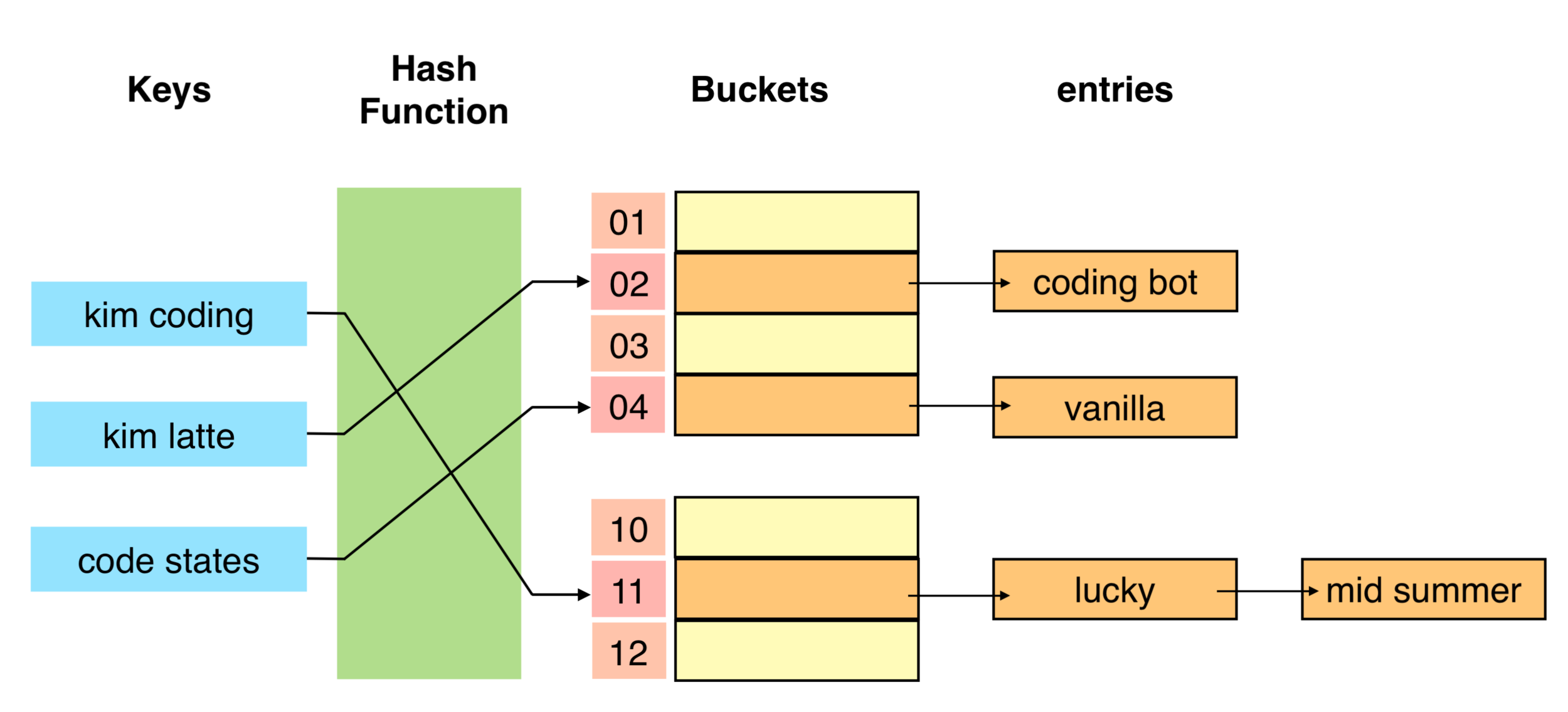
위의 그림처럼 저장소의 동일한 버킷의 데이터에 연결리스트(linked list), 트리(red-black tree)등의 자료구조를 사용해서 충돌이 일어난 데이터를 저장하는 방식. 이 방식의 경우 구현이 간단하며, 데이터를 쉽게 삭제할 수 있다는 장점이 있음. 하지만 중복으로 저장된 데이터가 많아지면 동일한 버킷에 연결되는 데이터가 많아져서 검색의 효율성이 감소한다는 단점이 있음.
- 저장소 확장(resize)
저장소에 크기가 작다면 불필요한 메모리 사용을 줄일 수 있지만, 해시 충돌이 발생하며 개방 연결법이나 분리 연결법을 사용해도 성능상 손실이 발생함. 실제 Java에서 사용되는 HashMap이라는 자료구조는 매치된 key-value 데이터 개수가 일정 이상이 된다면 (저장소의 75% 이상 사용) 저장소의 크기를 두 배로 늘리게 됨. 이 방식으로 해시 충돌로 인한 성능이 감소하는 문제를 어느 정도 해결이 가능.
Hash Table의 실사용 예제
- Address Book(주소록)
- Blockchain(블록체인)
- 자바스크립트 실행 엔진(크롬, V8)
- Domain -> DNS 변환
Heap Tree
Heap Tree의 정의
heap tree는 트리 구조로 구현된 자료구조. 일반적인 트리 구조와는 다르게, heap tree는 우선순위에 따라서 빠르게 자료를 검색할 수 있는 구조 임.
예. 응급실에서 환자가 들어올 때 환자가 들어온 순서와 달리 조금 더 빠른 치료가 필요한 환자부터 치료를 시작하게 되는 것
heap tree의 구조
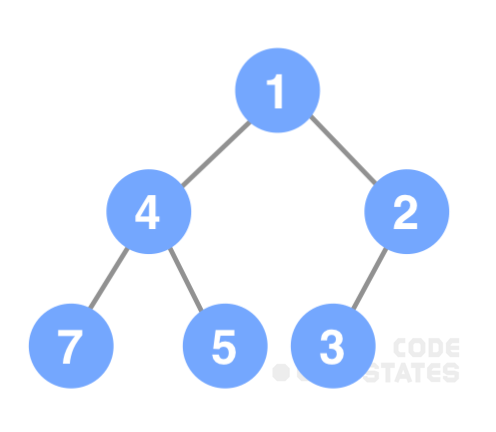
heap tree는 느슨한 정렬 구조로 구현 되어 있음: 부모 노드의 값은 자식의 값보다 항상 크거나 항상 작게 정렬되어 있지만 자식 노드끼리의 값의 크기에 따라 좌우 위치는 정렬하지 않기 때문에 느슨한 정렬 구조라고 표현함.
heap tree의 특징
-
완전 이진 트리: 단순히 최대값, 최소값을 찾기 위해서는 완전 이진 트리로 구성할 필요는 없지만, 삽입/삭제 시 성능을 위해 완전 이진 트리로 구현하게 됨.
-
중복된 값 저장: 일반적인 이진 탐색 트리와 다르게 중복된 값을 저장할 수 있음. 단순히 최댓값/최솟값을 찾아내기 위한 구조이기 때문.
-
최대 힙/ 최소 힙: 루트 노드에 가장 큰 값이 위치하며 자식 노드로 내려갈수록 작은 값이 위치하게 구현한다면 최대 힙이 되고, 루트 노드에 가장 값이 위치하며 자식 노드로 내려갈수록 큰 값이 위치하게 구현한다면 최소 힙이 됨.
heap tree의 데이터 처리 방식
- 데이터 검색(최대값/ 최소값)
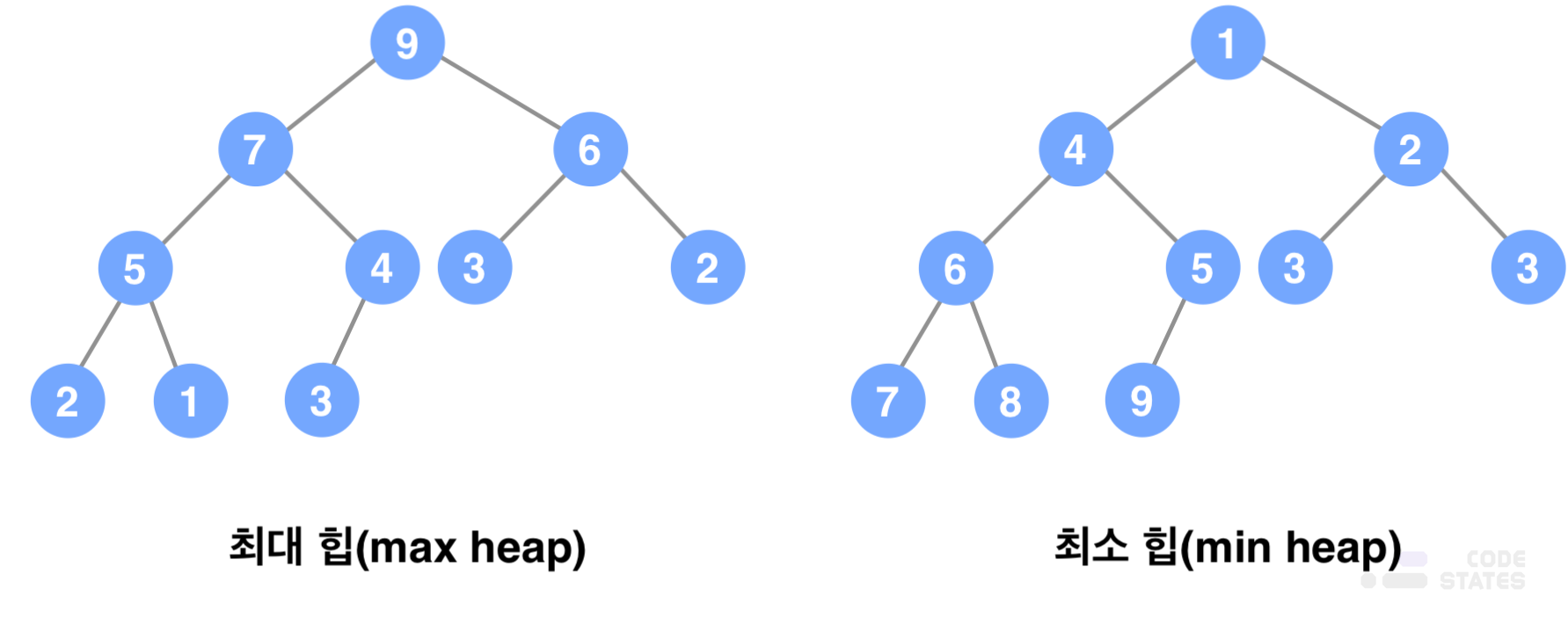
- 최대 힙일 경우 최대값을 찾는데 걸리는 시간복잡돈느 O(1). heap tree 특성상 최대 힙일 경우 항상 루트 노드의 값이 가장 큰 값이기 때문에 최대값은 항상 루트 노드의 값을 불러오기만 하면 됨.
- 최소 힙일 경우도 마찬가지로, 루트 노드의 값이 가장 작은 값이기 때문에 동일하게 O(1)의 시간복잡도를 가지게 됨.
- 데이터 삽입
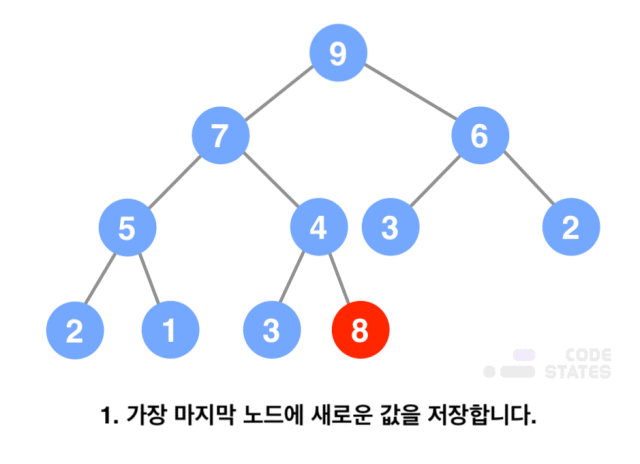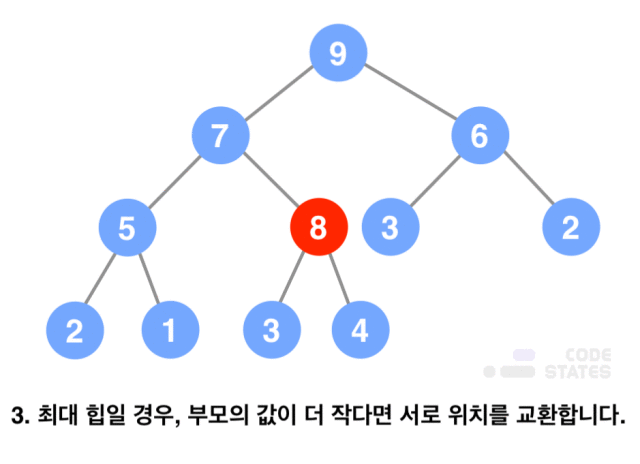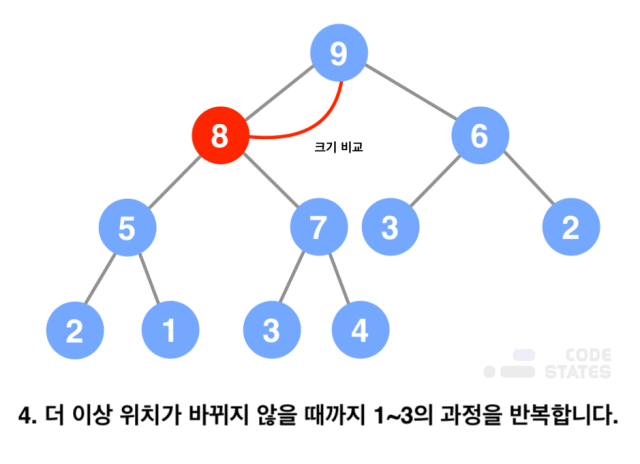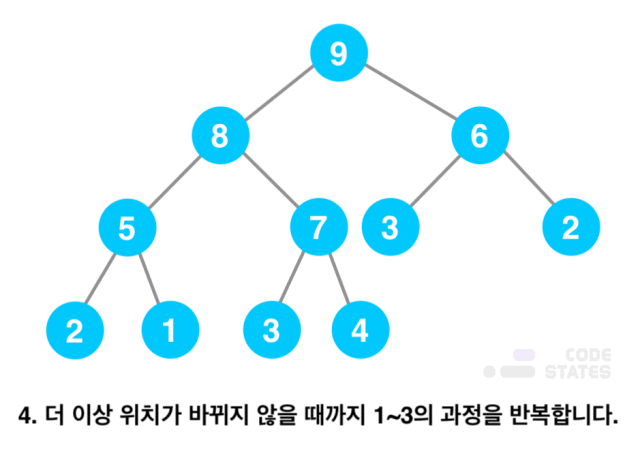
- 가장 마지막 노드에 새로운 값을 저장함
- 삽입된 노드의 값과 부모 노드의 값을 비교함
- 최대 힙일 경우, 부모의 값이 더 크다면 부모의 값과 위치를 서로 변경함
- 더 이상 위치가 바뀌지 않을 때까지 위의 과정을 반복함
- 데이터 삭제
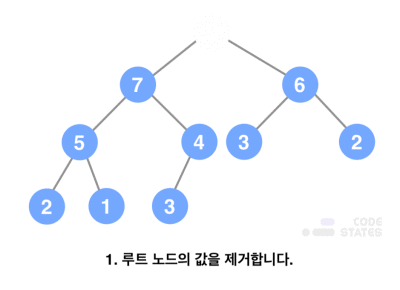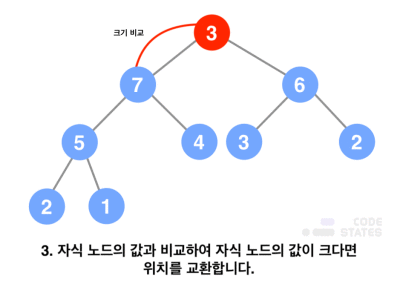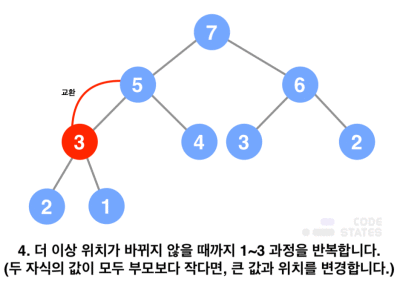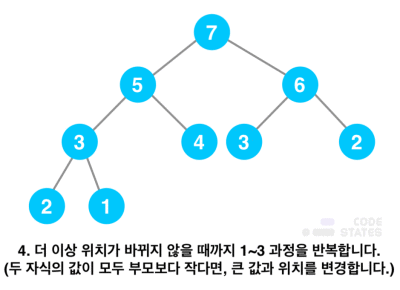
- 루트 노드의 값을 제거함
- 루트 자리에 마지막 노드의 값을 삽입함
- 올라간 노드의 값과 그 자식 노드들의 값을 비교함
- 부모보다 더 큰 자식이 있다면(최대 힙) 해당 자식의 값과 서로 교환함(만약 두 자식의 값이 모두 부모보다 작다면, 두 값 중 큰 값과 위치를 변경함)
- 더 이상 큰 값이 없을 때까지 반복함
heap tree를 배열로 구현하기
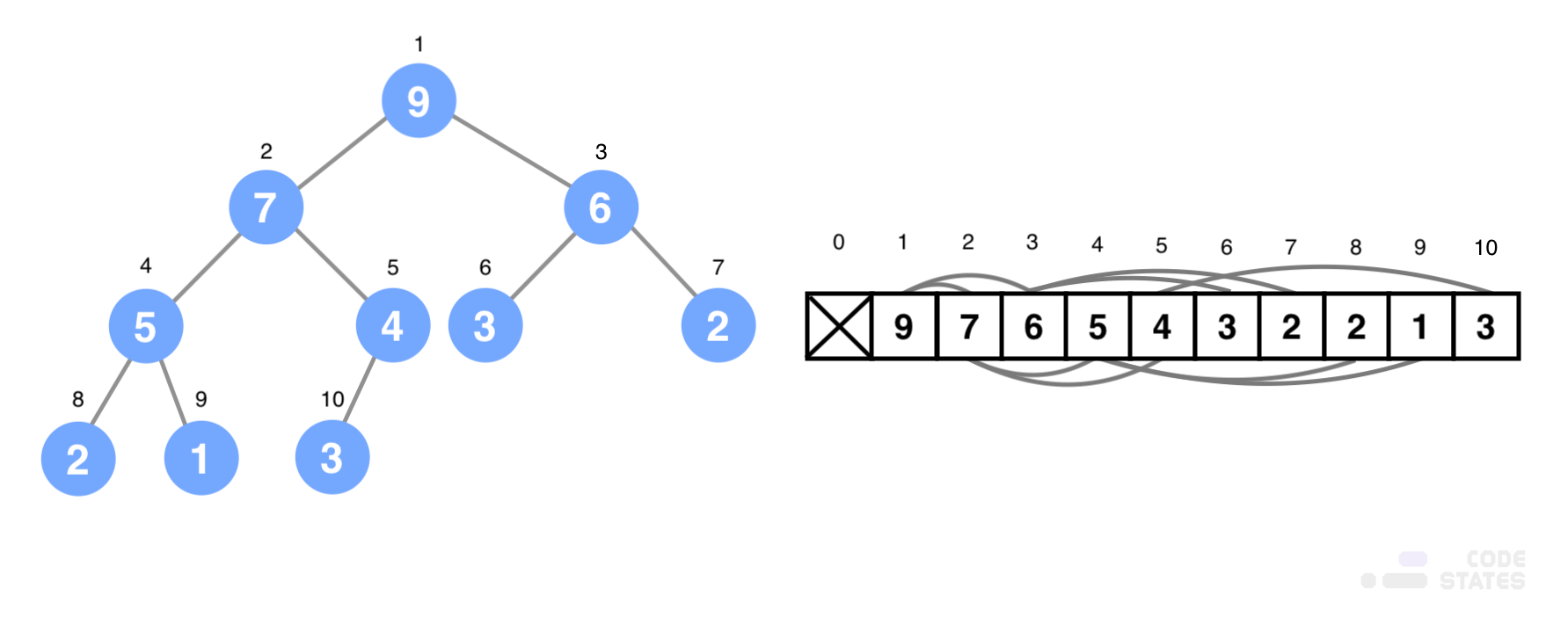
- heap tree는 완전 이진 트리로 구현되어 배열로 표현할 수 있음
- 완전 이진 트리의 특성상 중간에 빈값이 없기 대문에 루트 노드부터 높이 순서대로 배열에 모두 정렬이 가능함
- 구현과 노드의 위치를 찾기 쉽게 하기 위해 일반적으로 배열의 0번째 인덱스부터 사용하지 않고, 첫 번째 인덱스부터 사용함
- 위의 그림처럼 높이 순서대로 배열에 값을 저장하며, 좌에서 우로 순서대로 값을 저장하게 됨
- 배열로 heap tree를 구현한다면 배열의 크기에 따라서 heap tree의 depth가 얼마인지, 부모와 자식 노드의 위치까지도 쉽게 검색할 수 있음
- depth(깊이)는 배열의 길이가 1, 3, 7, 15 순서대로 2의 배수를 게속 더한 만큼 depth(깊이)가 늘어남
- 부모와 자식 노드의 인덱스를 찾는 방법도 수식으로 계산할 수 있음
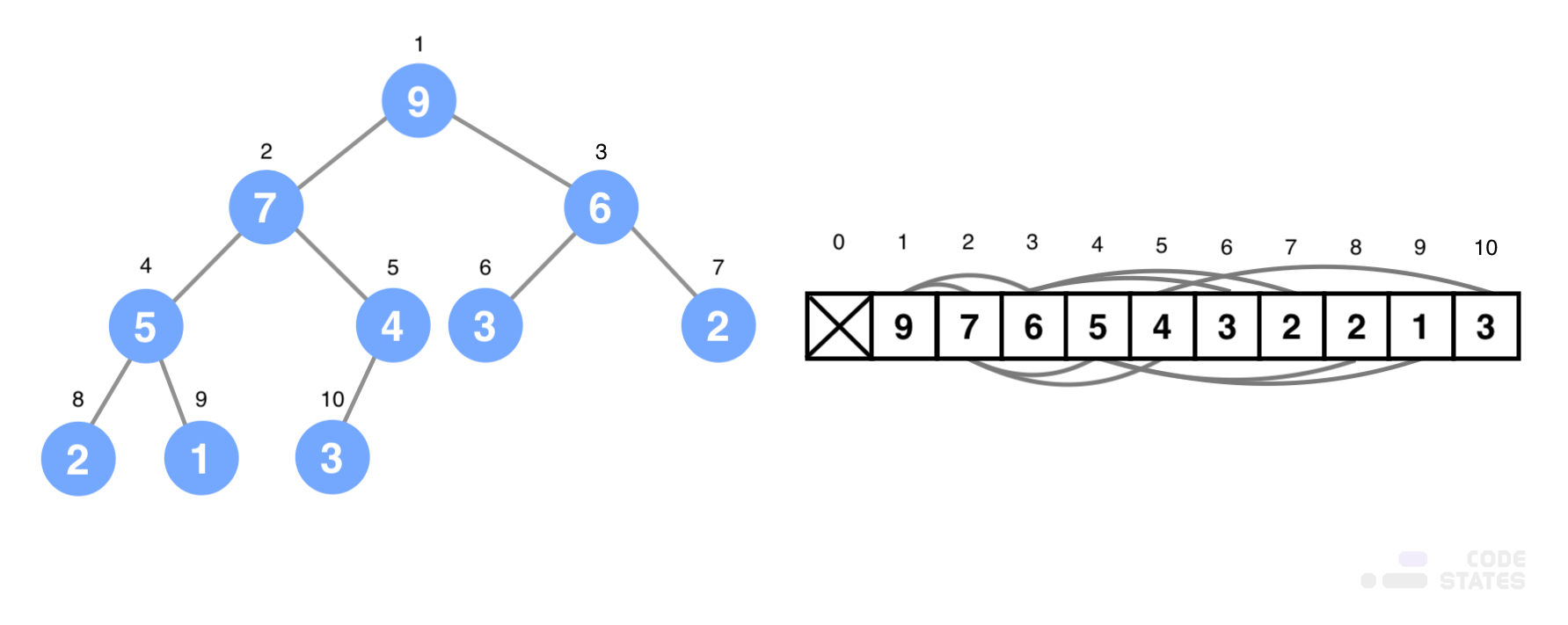
- 현재 노드의 왼쪽 자식 노드의 인덱스는 '현재 노드의 인덱스 * 2'
- 현재 노드의 오른쪽 자식 노드의 인덱스는 '(현재 노드의 인덱스 * 2) + 1'
- 부모의 인덱스는 '자식 노드의 인덱스 / 2' (내림)
heap tree가 사용되는 곳
- 우선순위 큐
- 힙 정렬