백준 2116번 : 주사위 쌓기(골드 5)

문제

풀이

오늘의 문제는 N개의 주사위를 세로로 쌓을 때 조건은 아래 층의 주사위의 윗 면과 윗 층의 주사위의 아랫 면이(즉, 닿아있는 주사위의 면) 숫자가 동일해야 한다는 것임

그렇게 쌓을 수 있는 경우의 수들이 만들어지면 4개의 옆 면이 만들어질텐데 각 옆 면들의 숫자의 합 중 최댓값이 될 수 있는 경우의 수를 구하는 것이다

그러면 옆면도 다 따로 생각해야할까?? 아니다. 문제에서 쌓은 주사위는 회전이 가능하다고 적혀 있다

그럼 그냥 조건에 맞게 주사위를 다 쌓고 각 주사위의 네 개의 면중 가장 큰 숫자만 선택해서 회전하면 그만이다

그래서 나는 가장 아래층의 주사위의 6개의 면을 윗 면으로 설정해 조건에 맞게 각 경우의 수를 찾으려고 한다

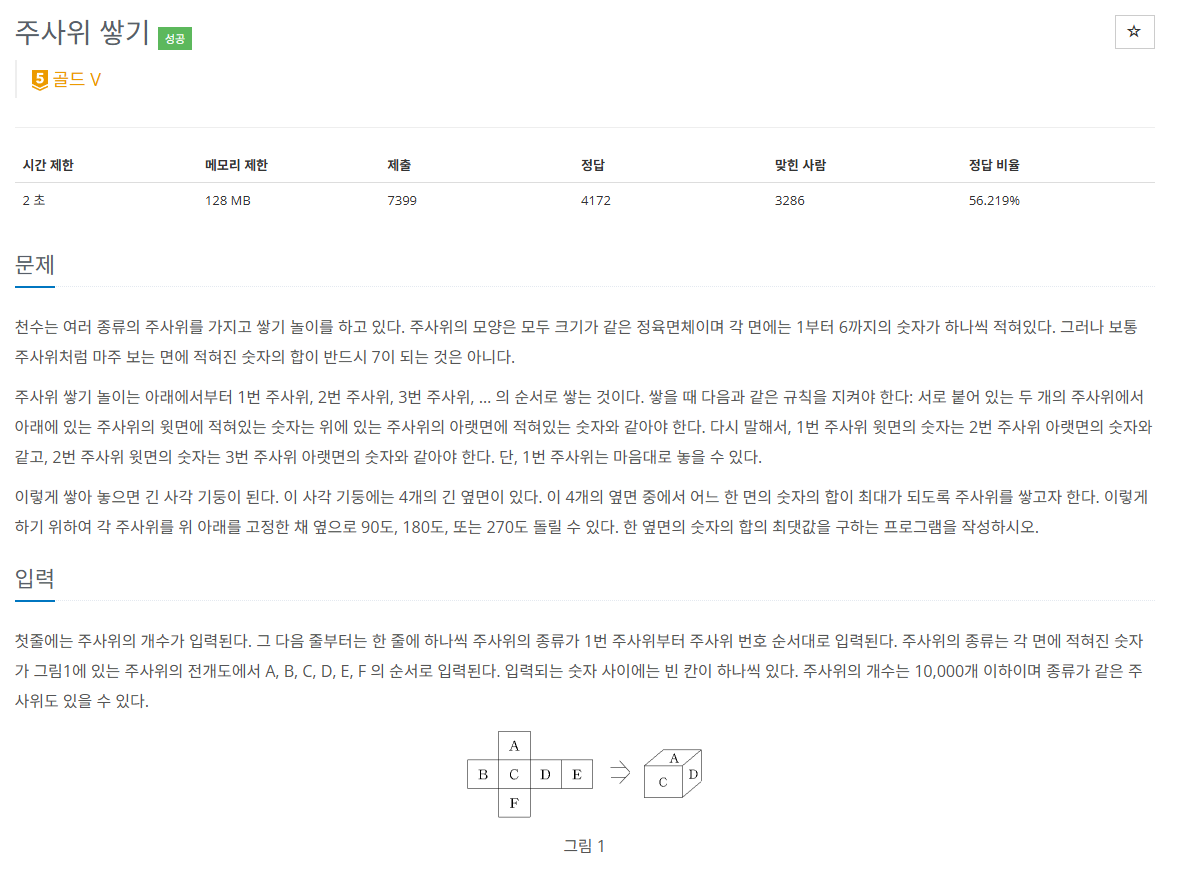
문제를 쉽게 풀기 위해 하나의 배열을 선언해주면 좋은데 바로 각 인덱스에 해당하는 반대편 인덱스를 매핑해두면 좋은 것이다. 주사위가 A, B, C, D, E, F로 입력받는데 A의 반대편은 F, B의 반대편은 D, C의 반대편은 E라서 다음과 같이 인덱스를 매핑했다

opposite[6] = {5, 3, 4, 1 ,2 ,0}

문제를 풀어보면 먼저 주사위를 입력받고 가장 아래층의 주사위는 조건이 없으므로 각 면을 윗 면으로 설정해 재귀 함수를 호출한다

재귀 함수의 정의는 void 함수(현재 주사위 인덱스, 현재 주사위의 윗 면의 인덱스, 지금까지의 합)이다

재귀 함수는 각자가 편한 방식으로 구현하면 된다. 무조건 남의 방식을 따라할 필요가 없음

그래서 나는 현재 주사위 인덱스가 N - 1에 다 다르면 정답을 업데이트해줄 것임

각 주사위를 방문하면서 자신의 주사위의 윗 면과 아랫 면을 제외한 최댓값을 리턴하는 함수 GetMaxSide를 정의했고 다음 주사위의 아랫 면의 인덱스를 받아와 다음 재귀 호출 시 opposite 배열을 사용해 윗 면의 인덱스를 구했다

코드

#include <bits/stdc++.h>
using namespace std;

int N;
int dice[10004][6];
int opposite[6] = { 5, 3, 4, 1, 2, 0 };

int answer;

void Input()
{
    cin >> N;

    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < 6; j++)
        {
            cin >> dice[i][j];
        }
    }
}

int GetMaxSide(int idx, int top)
{
    int ret = 0;

    for (int i = 0; i < 6; i++)
    {
        if (i == top || i == opposite[top]) continue;
        
        ret = max(ret, dice[idx][i]);
    }

    return ret;
}

void Func(int current, int top, int sum)
{
    if (current == N - 1)
    {
        answer = max(answer, sum + GetMaxSide(current, top));
        return;
    }

    int max_side = GetMaxSide(current, top);
    int next_bottom = 0;

    for (int i = 0; i < 6; i++)
    {
        if (dice[current][top] == dice[current + 1][i])
        {
            next_bottom = i;
            break;
        }
    }

    Func(current + 1, opposite[next_bottom], sum + max_side);
}

void Solve()
{
    for (int i = 0; i < 6; i++)
    {
        Func(0, i, 0);
    }
    
    cout << answer;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    Input();

    Solve();

    return 0;
}

회고

주사위의 수가 10000개까지이고 6개의 면만 확인하면 되므로 그렇게 시간 복잡도가 큰 문제는 아니었다

입력이 커지고 분기가 많아지면 백트래킹이나 DP를 활용해 최적화가 필요할 수도 있음

처음에 반대편 인덱스를 구하는 배열을 잘못 잡아 좀 헤맸다