0-1 KnapSack Problem
흔히 배낭 알고리즘이라고 불리는, 이 문제는 n개의 물건과 배낭이 있을 때, 물건에는 각각 무게와 가치가 있다
배낭에 들어갈 수 있는 최대 무게가 있어 배낭의 최대 무게를 초과하지 않으면서 물건들을 배낭에 담아 만들 수 있는 최대 가치의 합을 찾는 문제이다
배낭 문제는 물건을 자를 수 있으면 Fractional KnapSack Problem이고, 자를 수 없으면 0-1 KnapSack Problem이다
여기선 자를 수 없는 경우를 다뤄보겠다
예제
접근
처음에는 우선순위 큐를 이용해 그리디로 접근하려 했다가 안된다는 걸 깨달았다
그래서 구글링을 통해 찾아보니까 DP로 풀어야 하고 이런 알고리즘을 푸는 방법이 따로 있다고 한다
배낭 알고리즘이 DP인 이유는
물건을 배낭에 넣느냐 마느냐에 관한 문제이다. 1번째 물건을 배낭에 넣느냐 마느냐, 두 번째 물건을 넣느냐 마느냐에 따라 최대 합이 달라짐
최대 K까지 담을 수 있는 배낭이 있고 물건을 담을 때 선택할 수 있는 경우의 수는 2개이다
- 물건을 넣어서 (배낭 최대 용량 - 선택한 물건의 무게)
- 물건을 안넣고 배낭 최대 용량
이 과정을 모든 물건에 대해 반복하는 것이다. 가방에 더 이상 공간이 없을 때까지
코드
#include <bits/stdc++.h>
using namespace std;
int N, K;
int W[104], V[104]; // i번째 물건의 무게, 가치
int dp[100004];
int main()
{
cin >> N >> K;
for (int i = 1; i <= N; i++)
{
int w, v;
cin >> w >> v;
W[i] = w; V[i] = v;
}
for (int i = 1; i <= N; i++)
{
for (int w = K; w >= W[i]; w--)
{
dp[w] = max(dp[w], dp[w - W[i]] + V[i]);
}
}
cout << dp[K];
return 0;
}
풀이
많은 풀이에서는 DP 배열을 2차원 배열로 해서 DP[i][w] : i번째 물건을 담았을 때, 무게 w에서의 최대 가치라고 설정하지만 1차원으로 최적화가 가능하다
dp[w]는 무게가 w일때 최대 가치이다
처음 dp 배열의 초기화는 0으로 한다. 하나도 안 담는 경우가 있으니까
그리고 dp 배열을 채울 때 1번째 물건부터 루프를 돌아가며 배열을 뒤에서부터 업데이트한다. 물건을 중복해서 넣는 것을 방지하기 위해서임
그림으로 나타내면
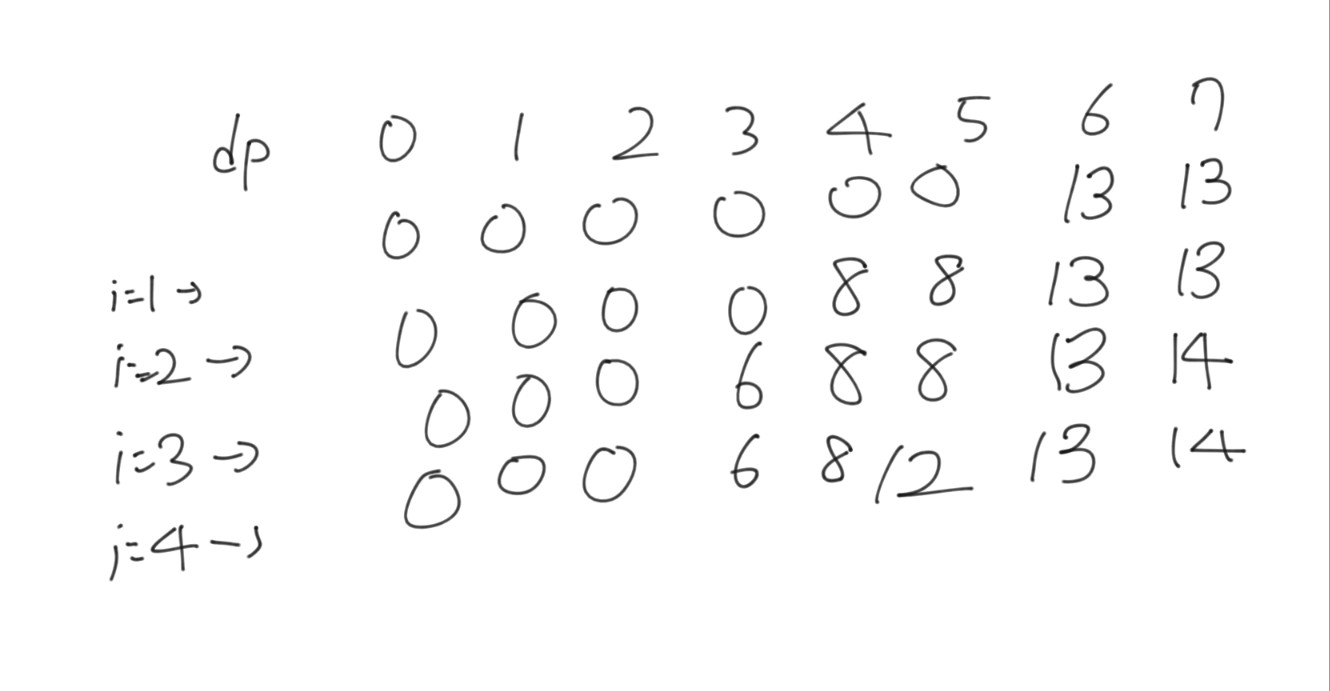
위에서부터 배열을 업데이트하며 마지막까지 했을 때 dp[K]가 답이다
참고
더 많은 지식은 다른 블로그에도 많으니까 참고하자!
https://howudong.tistory.com/106#article-1-1--0-1-knapsack-problem
