Community Detection in graph

1차 출처 : Label propagation algorithm / https://towardsdatascience.com/large-scale-graph-mining-with-spark-part-2-2c3d9ed15bb5
2차 출처 : Community Detection in graph / https://arxiv.org/pdf/0906.0612.pdf

---

들어가기에 앞서,

• 많은 Community Detection Alogrithms 가 있다.
• 대표적으로 Louvain 알고리즘이 있는 듯 하다.

---

라벨 전파 알고리즘이란?

• 준지도학습
• 쉽고 빠르다.
• 인접한 노드를 같은 라벨로 전파한다.
• (엣지의 weight가 1이라면) 맨 처음 라벨이 부여된 노드 기준, 모든 노드에 대해서 몇 다리 건너에 있는지 거리를 구할 수 있다.
• 마찬가지로 모든 노드에 대해서, 각자 노드끼리 얼마나 먼지 거리를 구할 수 있다.
• 이제 이 거리를 기준으로 0~1 의 값을 부여하고 확률로 간주한다.
• 구체적으로 모든 경우의 수에 해당하는 각 거리 합을 나눠줌으로써 가능하다.
• 이제 확률적으로 노드를 전파한다.
• N회 반복하면 수렴한다.

---

Modularity 개념이란?

• 그래프 분할시 잘 분할 되었는지/안되었는지 척도
• 잘 분할되면 높은 숫자 ( 1에 가까움 ) , 잘 안되면 낮은 숫자 ( -1 )에 가까움
• 클러스터링이 끝난 라벨이 주어진 그래프에 대해서
• 각 라벨별로 그룹 내부에 ( 실제로 연결된 edge 개수 - 그룹 내 연결된 edge 기대값 ) 값이 크면 오밀조밀 잘 연결되었다 = 잘 분할되었다

출처 : https://jimmy-ai.tistory.com/15

---

3. Community detection 의 구성요소 ( elements )

그래프 클러스터링에서의 문제점은

• 직관적으로 떠오르는 문제점은 "그래프 클러스터링" 의 정의가 모호하다.

커뮤니티(를 구분짓는)의 속성이나 파티션은 추상적이다.

중요하게 강조하고 싶은점은 구조적인 클러스터링의 정의 는 만약 그래프가 sparse 한 경우에만 가능하다는 점이다.

4. 전통적인 기법

4-1. 그래프 분할

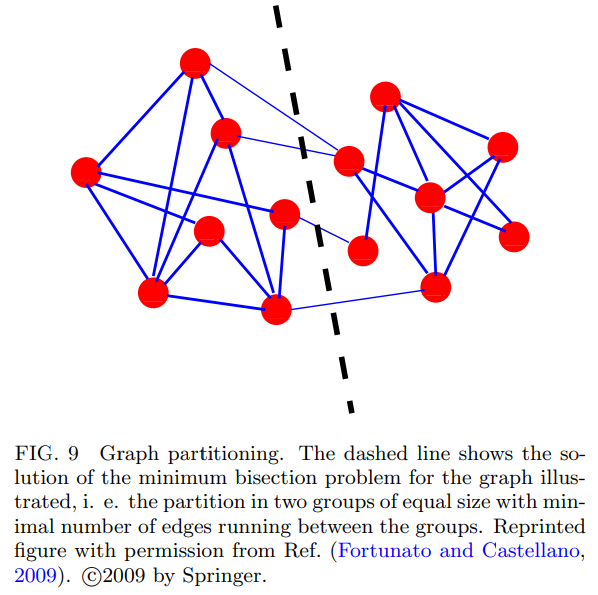
• 그래프 분할은 NP Hard 문제이다.