Isolation Forest / Extended Isolation Forest

2400·2023년 6월 6일

출처 : Extended Isolation Forest with Randomly Oriented
Hyperplanes : https://ieeexplore.ieee.org/ielaam/69/9371488/8888179-aam.pdf

IF ( Isolation Forest )

N 차원 공간을 분할할때 (Binary Serach Tree), 일차적인 가정은 "상대적으로 소수이면서 다른" 것들은 쉽게 분류 되며, "정상적인" 것들은 시작 노드로부터 스플릿 포인트가 많이 될 수 밖에 없다는 것이다.

직관적으로 밀도가 높은 영역에 있는 포인트들은 정상이라고 가정해보자.
밀도가 높은 영역의 한 점에 ( 다른 점과 닿지 않으면서 ) 도달하기 위해선 overfitting 되듯 스플릿이 많이 될 수 밖에 없을 것이다.
BST 는 인풋 데이터의 모든 점들을 isolate 하기 위해서 분할한다.
이후, 분할 횟수 ( 시작 노드로부터의 거리 )

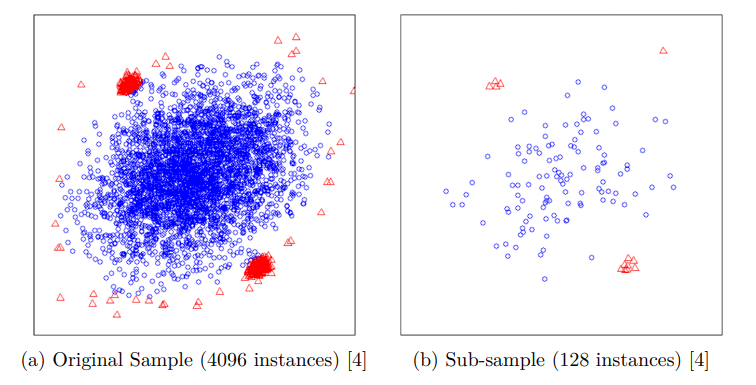
Isolation Forest 에서는 Robust 한 성능을 위해서 Sub-Sampling을 진행한다.

Isolation Forest 내부적으로 사용하는 Anomaly Score 는 아래 식으로 계산된다.

Anomlay Score
여기서 c(i) 는 Scale 보정을 위한 수로 보여진다. i개 row에 대해서 BST 를 진행했을때 unsuccessful 서치를 할 경우 평균적인 트리 깊이를 의미한다.
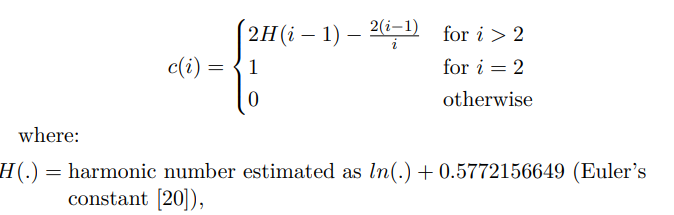
스코어의 형태를 보면 지수 형태이며 승수는 평균적인 트리 깊이의 "음수"이다.
즉, 깊이가 깊을수록 Score는 낮아지도록 설계되었다.
깊이가 깊을수록 0.5 보다 기하급수적으로 낮아지며
깊이가 얕을수록 0.5 보다 기하급수적으로 높아지며 1에 매우 가까운 숫자가 된다.ㅊ

IF 알고리즘

모든 점에 대해서 Isolation 되었거나, 한계 깊이에 도달한 경우 현재 깊이를 리턴한다.
sub-sampling 된 인풋 배치에서 변수 하나에 대해서 min~Max 사이의 랜덤한 스플릿 포인트 p를 정한다.
좌측 child 후보 군 선정 : ( p 값 이하에 해당 )
우측 child 후보 군 선정 : ( p 값 초과에 해당 )
스플릿 정보를 리턴한다. { 다음 깊이의 좌측 child / 다음 깊이의 우측 child / 현재 분할한 변수 feature ( attribute, q ) / 분할 지점 ( splitValue, p }

IF 의 장단점
장점

EIF 는 IF 의 일반화된 알고리즘이다.

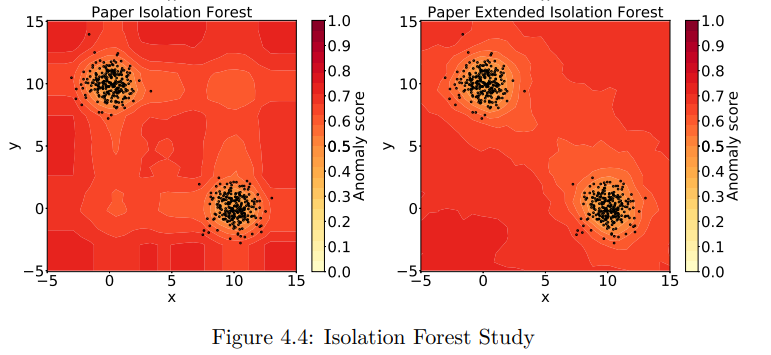
좀 더 구체적으로 EIF 에서는 Rotated Trees를 사용한다.

IF 는 트리 생성 전, 미리 sub-sample 된 데이터를 생성한다.
그런데 EIF 에서 sub-sample 된 데이터에 대해서 랜덤하게 twist 했을때 약간의 성능 향상은 있었지만 다음과 같은 문제점들이 있었다.
n개의 tree가 있고, n개의 sum-sample된 데이터가 있을때 각각 unique하게 twist가 되므로 anomaly Score 를 평균 냈을때 n개의 데이터 셋에 대해서 bias가 다른 문제가 있었다.
그리고 대용량/대차원 데이터에 적용하기 어려움이 있었다. ( 고차원 벡터를 rotation 변환한다고 생각해보면 메모리 사용량이 많을 것 같기도.. )
고차원으로 갈수록 rotation 이 2차원에서의 rotation 만큼 obvious 하지 않았다.
그래서 split line 을 random slope 가 되도록 하는 안을 선택했다.
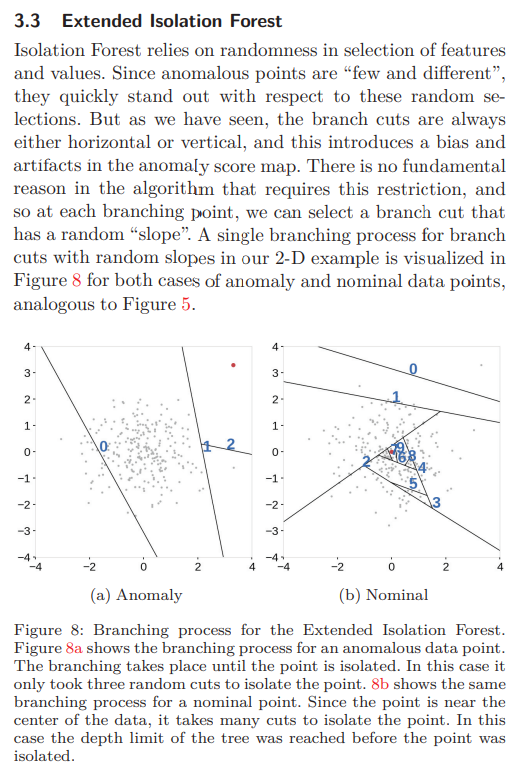
N차원 데이터에서 분할을 위한 랜덤 slope를 고르는 것은 unit N-Sphere 에서 uniform 하게 noraml vector를 고르는 것과 같다.
( * 여기서 normal vecotr 는 법선 벡터를 의미한다. )
( 왜 갑자기 normal vector 를 고른다는 이야기가 나올까? )
법선 벡터를 고르는 것은 표준 정규 분포에서 고르는 것과 같다. (?)
그리고 법선 벡터 기준으로 left child / right child 를 고르는 것은 법선 벡터의 내적이 0인 것을 이용하여, 내적 값이 0보다 작냐/크냐 기준으로 고를 수 있다.

2차원 데이터에선 직선이 split line 이었다. ( 2 - 1 ) 차원.
고차원 데이터에선 ( N - 1 ) 차원의 hyperplane 으로 분할되는데, hyperplane 이 꼭 고차원일 필요가 없듯이, 0~N-1 구간에서 랜덤하게 선택한다.

공부용 혹은 정리용 혹은 개인저장용