Ref : 만화로 배우는 베이즈 통계학
정상적인 주사위와 조작된 주사위가 있다.
조작된 주사위는 특정 눈(1,2,...,6)의 확률이 1/6 이 아니다.
그렇다면 조작된 주사위와 정상적인 주사위의 확률분포가 유사한 정도는 어떻게 표현할까?
KL-D 로 계산한다.
KL-D의 식은 꽤 비직관적이다.
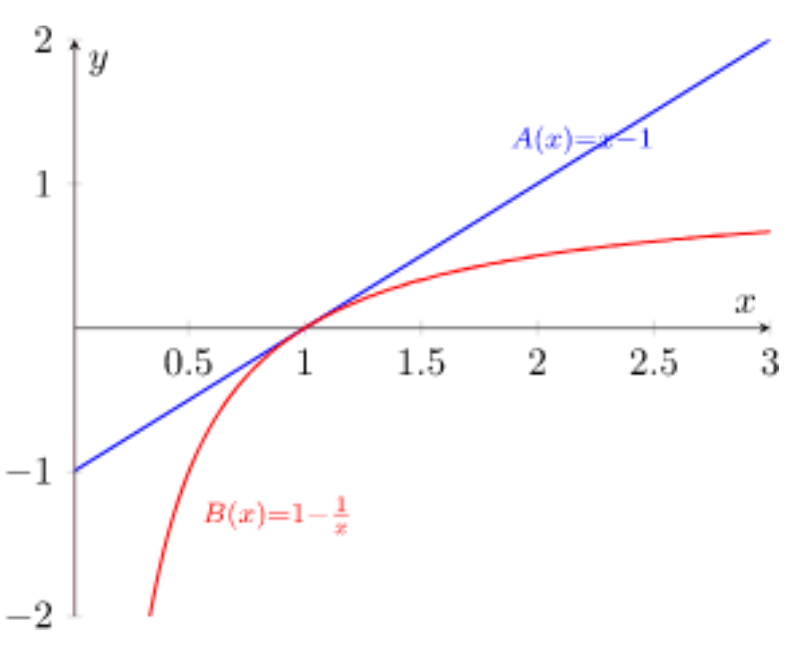
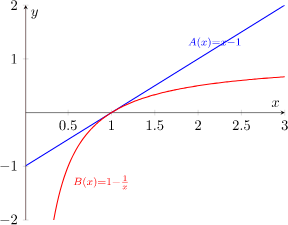
위 그래프에서 빨간 선이 log x 라고 하자.
logx <= x-1 라는 사실은 이미 알려져 있다.
다시 KL-D로 돌아와서,
P_t : t 일때 확률 P ( 조작된 주사위의 눈을 굴렸을때 특정 눈(t)이 나올 확률 )
S_t : t 일때 확률 S ( 정상 주사위의 눈을 굴렸을때 특정 눈이 나올 확률 )
P_t = S_t * ( P_t / S_t ) 이다.
분자로 나눠주고 다시 분모에 곱해준 형태이다.
그럼 이러한 P_t 를 다 더해보자.
sigma( P_1. P_2, ... P_t, ... P_6 ) = sigma ( S_t(P_t/S_t) ) 이다.
앞서 logx <= x-1 임을 확인했다.
따라서,
sigma ( log( S_t * ( P_t/S_t) ) <= sigma ( S_t(P_t/S_t) - 1 ) 이다.
그런데, sigma( P_t ) = 1 이다.
sigma ( log( S_t * ( P_t/S_t) ) <= 0 임을 알 수 있다.
이젠 부등호 양 변에 -1을 곱해보자.
Before : sigma ( log( S_t ( P_t/S_t) ) <= 0
After : sigma ( log( S_t ( S_t/P_t) ) >= 0
그러고나서 log 쪽 값을 분해해보자.
Before : sigma ( log( S_t ( S_t/P_t) ) >= 0
After : sigma ( log( S_t S_t ) - log( S_t * P_t ) ) >= 0 임을 알 수 있다.
마지막 식 : sigma( log( S_t S_t ) - log( S_t P_t ) )
형태가 KL-D 식이다.
KL-D 가 0이 되는 시점은 S_t = P_t 되는 시점이다.
이로써,
KL-D(S,P) 의 값이 작을수록 P_t 가 S_t 와 가까운(유사한) 확률 분포를 가졌다고 볼 수 있는 것이다.
