
알고리즘 문제 풀이 스터디를 하며 만든 자료입니다.
개인 공부 기록용으로 올립니다.
Graph 란?
그래프는 정점(Vertex, 또는 노드(Node)라고도 함)과 이들을 연결하는 간선(Edge)로 구성된 비선형 자료구조
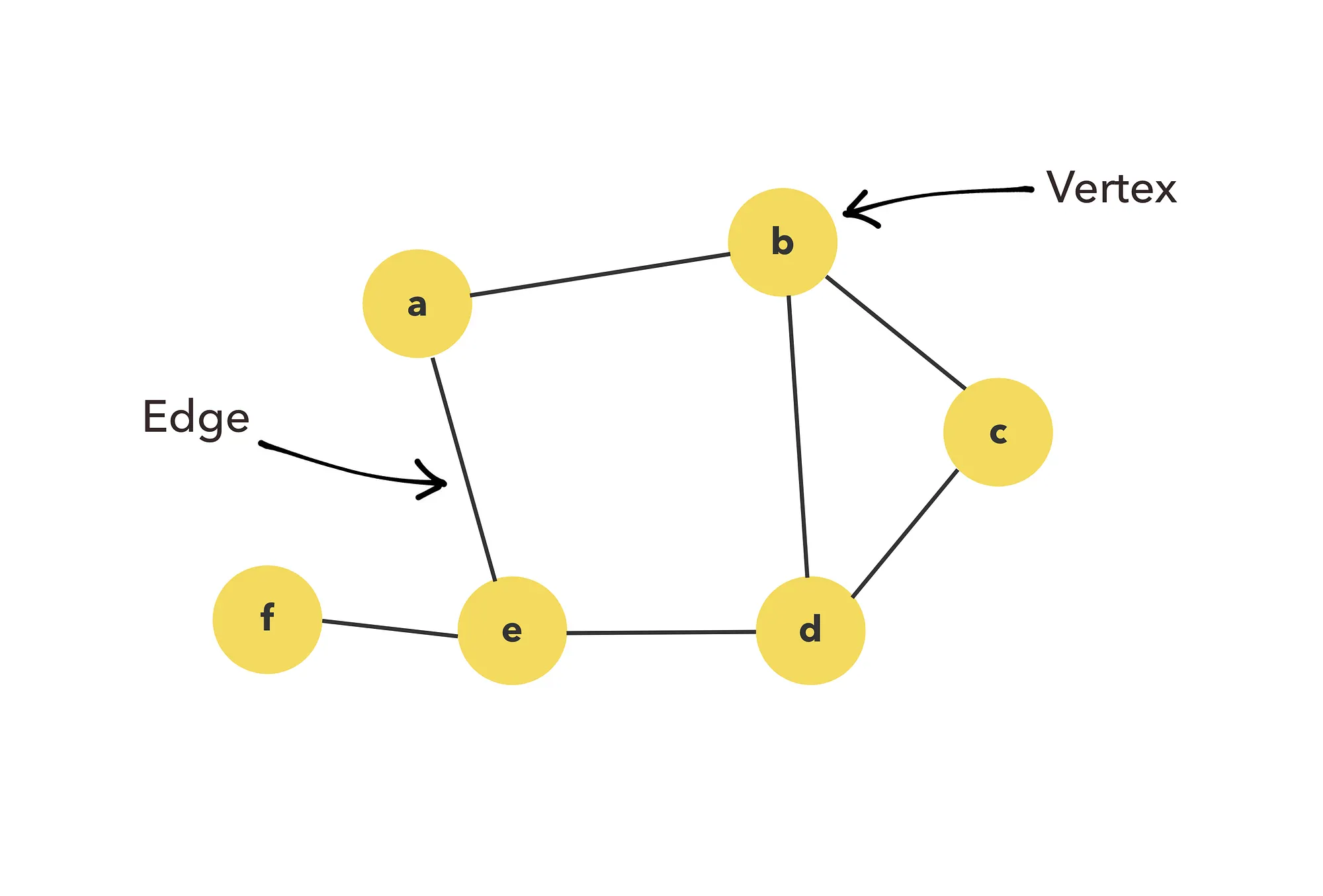
Graph 용어 정리
간략한 그래프 용어 정리
| 용어 | 설명 |
|---|---|
| 정점(Vertex), 노드(Node) | 그래프에서 간선이 만나는 지점 하나의 점으로, 데이터 저장시 사용 |
| 간선(Edges) | 노드 간의 관계 또는 연결을 나타내는 선 |
| 차수(Degree) | 노드에 연결된 간선(Edge)의 개수 (방향 그래프에서는 in-degree, out-degree로 나뉨) |
| 가중치(Weight) | 간선에 부여된 값 (예: 거리, 비용 등), 특성을 나타냄 |
| 사이클(Cycle) | 같은 노드으로 되돌아오는 경로(시작 노드와 끝 노드가 동일한 경로) |
예시
- 정점 : 장소
- 간선 : 길
- 가중치 : 거리/요금
Graph의 특징
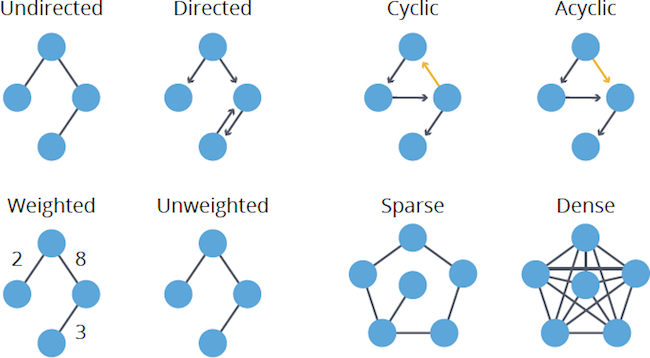
- 방향성 : 방향(Directed) / 무방향(Undirected)
- 사이클 유무 : 사이클(Cyclic) / 비사이클(Acyclic)
- 가중치 유무 : 가중치(Weighted) / 무가중치(Unweighted)
- 간선의 밀도 : 밀집(Dense) / 희소(Sparse)
Graph 구현 방법
그래프를 표현하는 대표적인 방식은 아래 두 가지입니다.
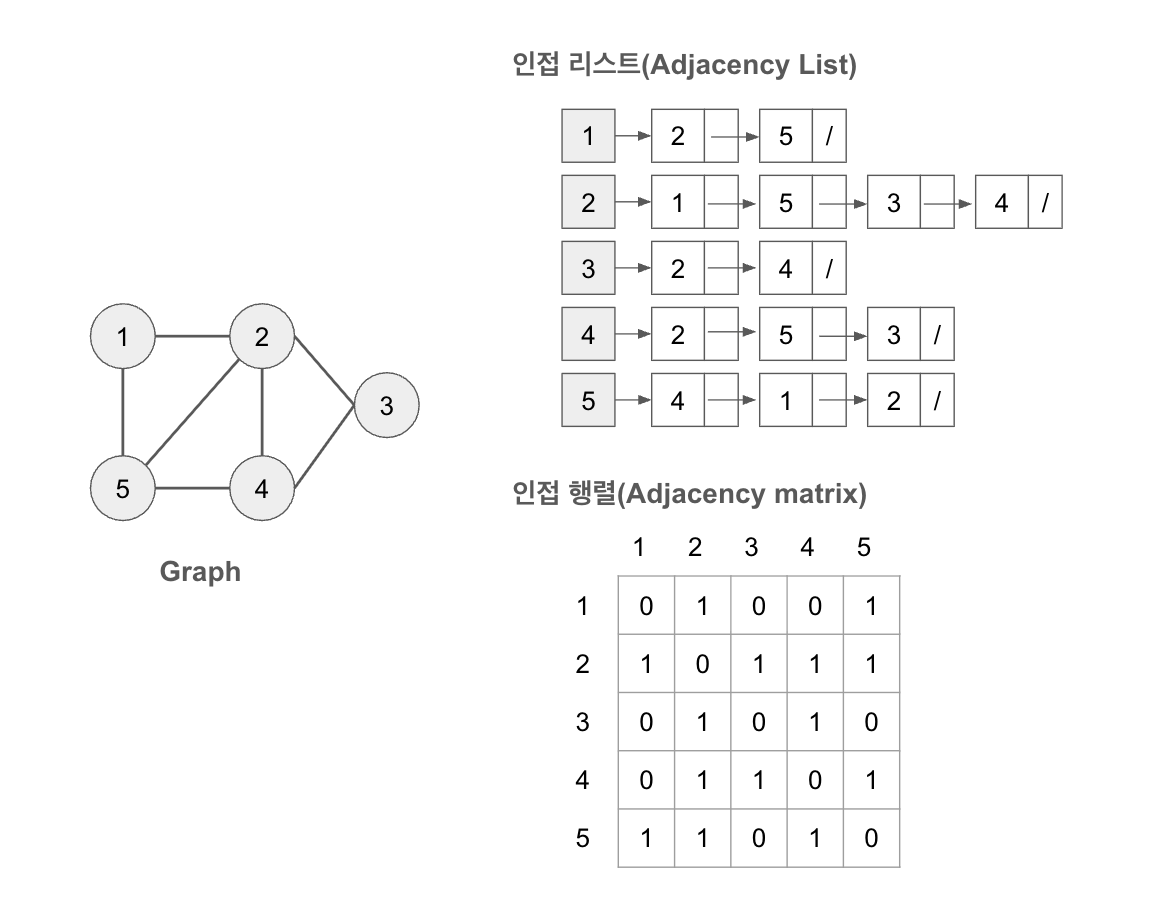
1. 인접 행렬 (Adjacency matrix)
관계를 2차원 배열로 표현
- 노드간 연결 여부를 빠르게 확인 가능
- 모든 노드의 관계를 행렬로 저장하므로 메모리 소비 큼
2. 인접 리스트 (Adjacency List)
관계를 링크드 리스트로 표현
- 배열 방에 노드를 나열, 연결되는 노드를 링크드 리스트로 쭉 나열
- 메모리 효율적, 연결된 정점 탐색에 유리
💡 언제 무엇을 사용할까?
간선(Edge)이 많은 밀집 그래프 → 인접 행렬(Adjacency matrix)
간선(Edge)이 적은 희소 그래프 → 인접 리스트(Adjacency List)
Graph 탐색 알고리즘
대표적인 그래프 알고리즘 3가지
- 그래프 탐색 : DFS , BFS
- 최단 경로 : Dijkstra
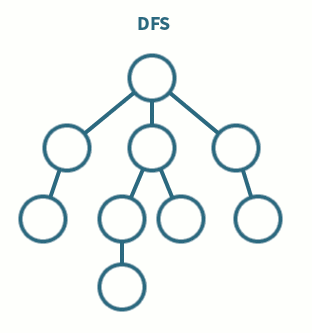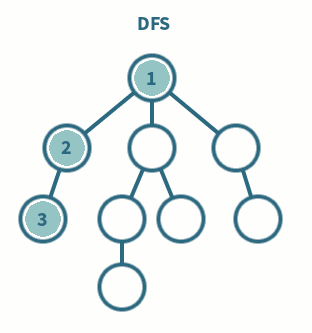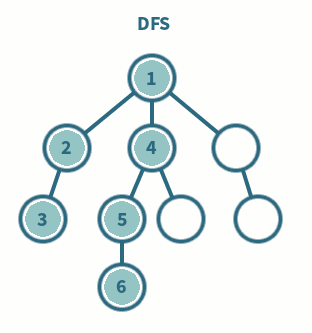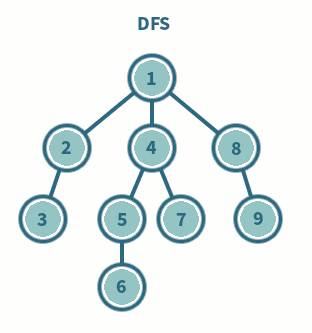
📌 DFS(Depth-First Search, 깊이 우선 탐색)
가능한 깊게 탐색한 후, 더 이상 갈 곳이 없으면 이전 정점으로 되돌아가는 방식
다른 경로로 넘어가기전 해당 분기를 완벽하게 탐색
⇒ 세로 탐색
- 주로 스택(Stack) 또는 재귀 함수로 구현
✅ 장점
- 현 경로상의 노드만 기억 ⇒ 메모리 효율 좋음
- 목표 노드가 깊은 위치에 있는 경우, 빠르게 도달 가능
❌ 단점
- 해가 없는 경로를 깊이 탐색할 수 있어 비효율적
- 최단 경로를 보장하지 않음
- 깊이가 깊으면 스택 오버플로우 위험
- ⚠️ 깊이 제한 두는 방법으로 해결할 수 있음
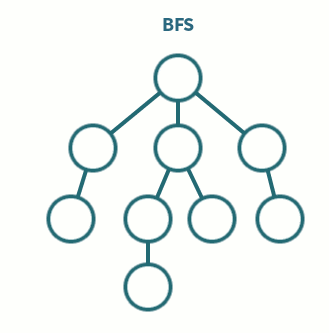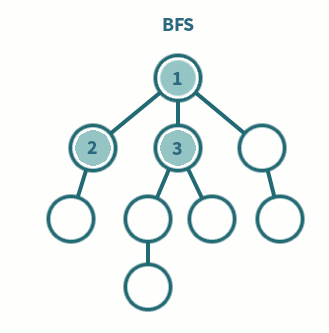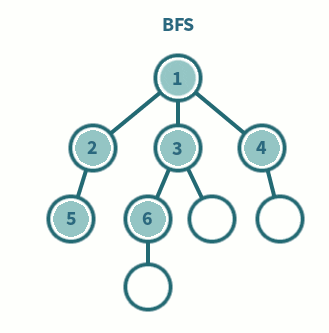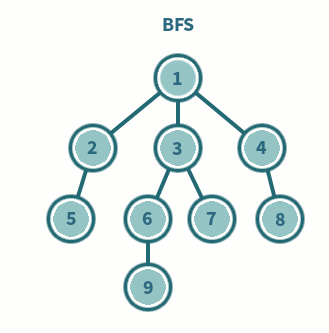
📌 BFS(Breadth-First Search, 너비 우선 탐색)
한 노드에서 시작해 인접한 노드부터 모두 탐색하고 이후 그 인접한 노드의 인접한 노드 반복… ⇒ 가로 탐색
- 주로 큐(Queue) 사용해 구현
✅ 장점
- 최단 경로 탐색에 유리(특히 무가중치 그래프)
- 경로가 무한히 깊어져도 반드시 해를 찾을 수 있음
- 노드 수가 적고 깊이가 앝은 해가 존재할 때 유리
❌ 단점
- 탐색을 위한 큐 사용 → 메모리 사용량 증가
DFS vs BFS
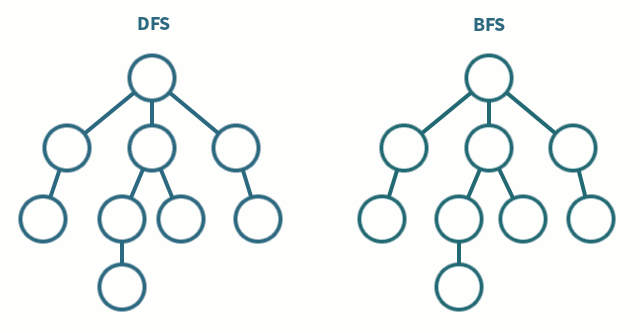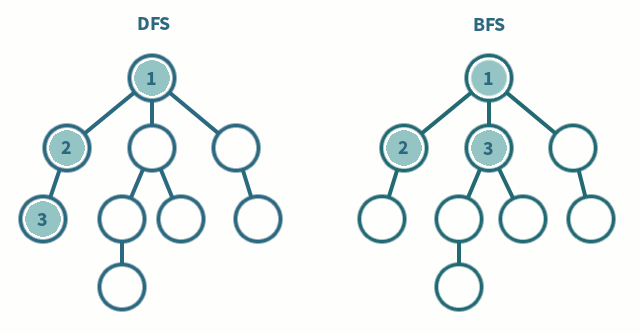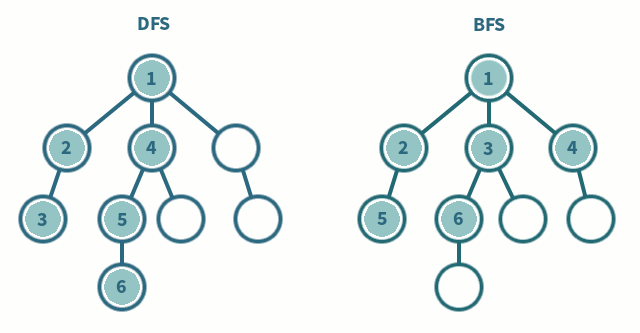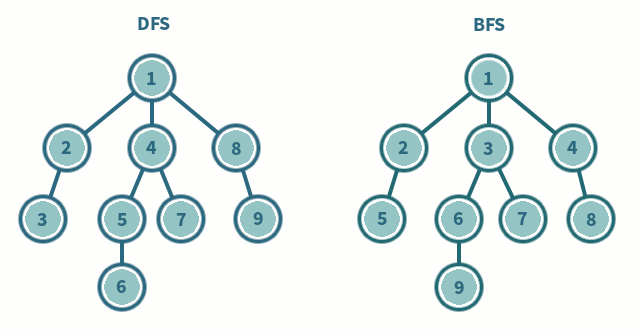
| DFS | BFS | |
|---|---|---|
| 탐색 방식 | 깊이 우선 분기마다 깊게 탐색 | 너비 우선 인접 노드부터 탐색 |
| 구현 방법 | 스택, 재귀 함수 | 큐 |
| 주 사용처 | 미로 찾기, 사이클 탐지, 백트래킹 | 최단 거리 탐색, 전염병 확산 시뮬레이션 |
| 메모리 | 호출 깊이만큼 사용 | 큐 크기만큼 사용 |
| 최단 경로 보장 | ❌ | ⭕️ |
DFS와 BFS의 시간 복잡도
- 인접 리스트 :
O(N + E) - 인접 행렬 :
O(N^2)
N: 노드의 개수, E: 간선의 개수
→ 일반적으로 인접 리스트 방식이 더 효율적
두 방식 모두 조건 내의 모든 노드를 검색한다는 점에서 시간 복잡도는 동일
BUT 일반적으로 DFS를 재귀 함수로 구현한다는 점에서 DFS보다 BFS가 조금 더 빠르게 동작함
📌 Dijkstra 알고리즘 (최단 경로 알고리즘)
그래프에서 한 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘
→ 매번 최단 경로의 정점을 선택해 탐색을 반복하는 것
- 우선순위 큐 (Heap) 활용 :
(O(E log V)) - BFS + DP 개념으로 이해하면 편함
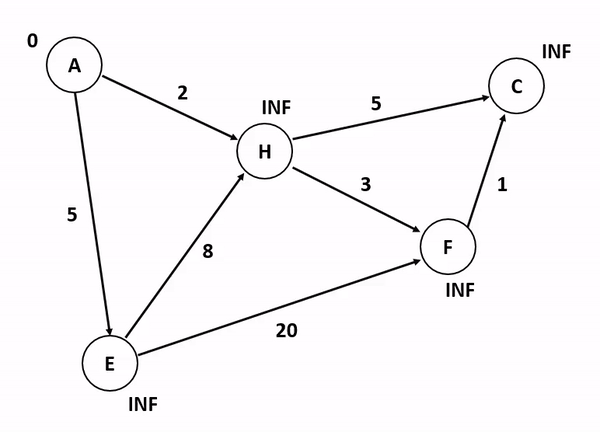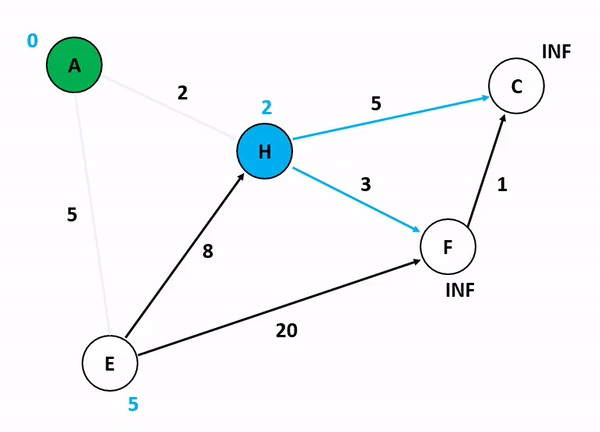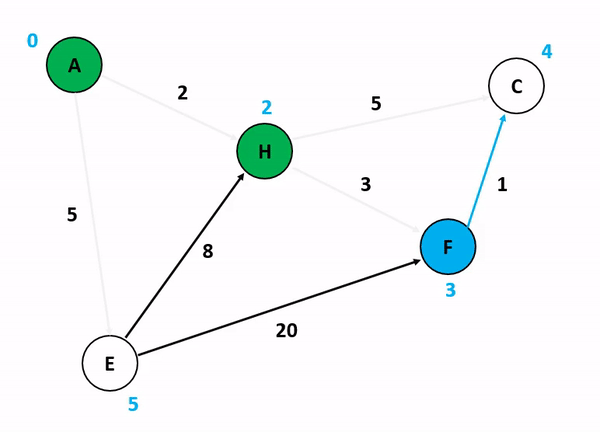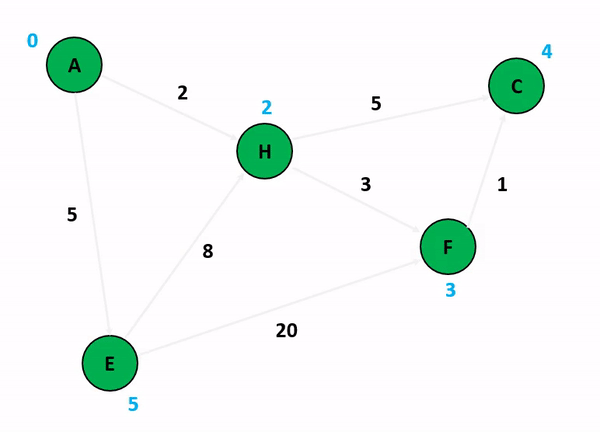
✅ 장점
- 거리뿐만 아니라 실제 경로 추적도 쉽게 구현 가능
- 가중치가 있는 그래프에서 안정적인 최단 경로 탐색이 가능
❌ 단점
- 간선(Edge)이 많은 대규모 그래프에서 큐 연산이 많아져 속도가 느려질 수 있음
- 그래프와 거리 정보를 저장해야 하므로 메모리 사용량이 많음
- 단일 최단 경로만 제공, 동일 거리의 경로가 여러 개 있어도 전부 찾지는 않음
실제 활용 사례
- SNS 친구 추천 → 그래프 탐색
- 지도앱 길찾기 → 다익스트라(Dijkstra)
- 게임 맵 탐색, AI 이동 경로 계산 → DFS / BFS
Graph 알고리즘 선택 가이드
| 알고리즘 | 특징 | 주 사용처 |
|---|---|---|
| DFS | 최대한 깊게 탐색 | 사이클 탐지, 경로 존재 여부 |
| BFS | 가까운 노드부터 탐색 | 최단 거리 탐색 (무가중치 그래프) |
| Dijkstra | 가까운 거리부터 최단 거리 갱신 | 실시간 길찾기 (가중치 그래프의 최단 경로 탐색) |