547. Number of Provinces

문제

각 도시의 연결 관계가 그래프의 인접행렬 형식으로 주어진다. 연결되어있는 모든 도시를 하나의 Province라고 할때, 총 Province의 갯수는?

Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

해결 아이디어

각 노드별로 백트래킹 형태의 dfs 순회를 한다.

해결

인접행렬의 DFS순회 코드 다시 살펴보기.

class Solution {
    vector<int> visit; // node already visited
    void mark_connection(vector<vector<int>>& graph, int from) {
        for (int i = 0; i < graph[from].size(); i++) {
            if (graph[from][i] == 0 || visit[i] == 1)
                continue;
            visit[i] = 1;
            mark_connection(graph, i);
        }
    }
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        int rsize = isConnected.size();
        visit = vector<int>(rsize, 0);
        int nr_province = 0;
        
        for (int i = 0; i < rsize; i++) {
            if (visit[i] == 1)
                continue;
            mark_connection(isConnected, i);
            nr_province++;
        }
        return nr_province;
    }
};

399. Evaluate Division

문제

["a", "b"] 데이터가 포함된 equations배열과, 같은 크기의 values 배열이 주어진다. values 의미는 각 index의 a / b를 계산한 값이다. 여기서 queries 로 전달되는 ["x", "y"] 값을 구하라.

Input: equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
Output: [6.00000,0.50000,-1.00000,1.00000,-1.00000]
Explanation: 
Given: a / b = 2.0, b / c = 3.0
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
return: [6.0, 0.5, -1.0, 1.0, -1.0 ]

해결 아이디어

• equations 으로 주어지는 데이터는 양방향 그래프로 표현될 수 있다.
• equations = [["a","b"], ...] 이고 values = [2.0, ...] 라고 할때, a -> b 의 엣지의 가중치는 2.0 그리고 b -> a 엣지의 가중치는 1/2.0 과 같다.
• 따라서 ["a", "x"]의 값은 a -> b -> .. -> x 의 과정중에 각 엣지 가중치를 곱한 결과와 동일하다.
• 흥미로운 문제였다!

해결

그래프의 자료구조를 참고하기 unordered_map<string, vector<pair<string, double>>> graph;
각 노드 string에 해당하는 노드의 인접리스트를 pair(string, double)타입 형태로 만들어서 각 노드로 향하는 가중치값고 가지게 만들었다.

class Solution {
    unordered_map<string, vector<pair<string, double>>> graph;
    unordered_map<string, bool> visited;
    vector<double> ret;
    
    void find_path(int ret_idx, string from, string tgt, double ratio) {
        if (visited[from] == true)
            return;
        if (from == tgt) {
            ret[ret_idx] = ratio;
            return;
        }
        visited[from] = true;
        for (int i = 0; i < graph[from].size(); i++) {
            find_path(ret_idx, graph[from][i].first, tgt, ratio * graph[from][i].second);
        }
        visited[from] = false;
    }

public:
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        ret = vector<double>(queries.size(), 0);
        /* generate a graph structure */    
        for (int i = 0; i < equations.size(); i++) {
            graph[equations[i][0]].push_back(make_pair(equations[i][1], values[i]));
            graph[equations[i][1]].push_back(make_pair(equations[i][0], 1 / values[i]));
        }
        
        for (int i = 0; i < queries.size(); i++) {
            if (graph.find(queries[i][0]) == graph.end() || graph.find(queries[i][1]) == graph.end()) {
                ret[i] = (double)-1.0;    
                continue;
            }
            find_path(i, queries[i][0], queries[i][1], 1);
            if (ret[i] == 0)
                ret[i] = (double)-1.0;    
        }
        return ret;
    }
};

210. Course Schedule II

문제

총 n개의 강좌 (0 ~ n-1)가 주어지고, 각각의 강좌는 사전수강 강좌가 있다. [강좌, 사전수강필요 강좌] 의 배열이 주어질때, 강좌를 수강해야할 순서대로 정렬하라. 만약 모든 강좌를 수강하는게 불가능하면 빈 vector를 리턴.

Input: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
Output: [0,2,1,3]
Explanation: There are a total of 4 courses to take. To take course 3 you should have finished both courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
So one correct course order is [0,1,2,3]. Another correct ordering is [0,2,1,3].

해결 아이디어 -> topological sort(위상정렬)

선후 관계가 정의된 그래프 구조상에서, 선후관계에 따라 순서를 정렬하는방법.

용어

• In-Degree(진입차수) : 특정 노드로 들어오는 간선 갯수
• Out-Degree(진출차수): 특정 노드에서 나가는 간선 갯수

알고리즘 BFS

1. 진입차수(In-degree)가 0인 노드를 큐에 push
2. 큐가 empty가 될때 까지 아래 반복
   a. 큐에서 pop한 노드의 나가는 간선 제거
   b. 새로 진입차수가 0이 된 노드 큐에 push

• 결과적으로 큐에서 pop한 노드의 순서가 Topology Sort된 순서.

구현

• 기본적으로 부모 노드가 없는 노드 순서로 정렬 하는것과 같다. 이것은 ->BFS로 풀수있다.
• 이를 거꾸로 하면 leaf노드 순서대로 정렬하고 반전하는것과 같다. 이것은 DFS로 해결할 수있다.

해결 DFS

dfs순회하면서 leaf 노드 순서대로 저장.

class Solution {
    vector<vector<int>> graph;
    vector<int> ret;
    vector<int> visited;
    
    bool is_cycle(int cur) {
        if (visited[cur] == 1)
            return true;
        if (visited[cur] == 0) {
            visited[cur] = 1;
            for (int i = 0; i < graph[cur].size(); i++) {
                if (is_cycle(graph[cur][i]))
                    return true;
            }
            ret.push_back(cur); // leaf first order -> topological sort
        }
        visited[cur] = 2;            
        return false;
    }
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        graph = vector<vector<int>>(numCourses);
        visited = vector<int>(numCourses, 0);
        
        for (auto it: prerequisites) {
            graph[it[1]].push_back(it[0]);
        }
        for (int i = 0; i < numCourses; i++) {
            if (is_cycle(i)) // if cycle exist, return an empty vector
                return {};
        }
        reverse(ret.begin(), ret.end());
        return ret;
    }
};

해결 BFS

진입차수가 0인 (부모노드가 없는) 노드 순서대로 저장.

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph(numCourses);
        unordered_map<int, int> indeg;
        vector<int> ret;
        
        for (auto it: prerequisites) {
            graph[it[1]].push_back(it[0]);
            indeg[it[0]]++;
        }
        queue<int> q;
        for (int i = 0; i < numCourses; i++) {
            if (indeg[i] == 0)
                q.push(i);
        }
        while (!q.empty()) {
            int tgt = q.front();
            q.pop();
            ret.push_back(tgt);
            for (int i = 0; i < graph[tgt].size(); i++) {
                int adj = graph[tgt][i];
                indeg[adj]--;
                if (indeg[adj] == 0)
                    q.push(adj);
            }
        }
        if (ret.size() == numCourses)
            return ret;
        return {};
    }
};

207. Course Schedule

문제

[강의, 사전수강필요 강의] 의 강좌 정보가 배열로 주어질때, 주어진 강좌를 모두 수강할 수 있는지 없는지 판단하라.

Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false
Input: numCourses = 4, prerequisites = [[1,0],[2,1],[2,0],[3,2]]
Output: true
Input: numCourses = 2, prerequisites = [[0,2],[2,1],[1,0],[3,2]]
Output: false

아이디어 -> Topology Sort (위상정렬)

• adjacent[사전수강강의] 에 해당하는 강의 리스트를 자료구조를 생성하면 , 방향성 그래프 자료구조가 된다.
• 만약 그래프에 사이클이 존재한다면, 모든 강좌를 수강할 수 가 없다는 뜻이다.
• 따라서 해당 그래프의 사이클의 존재유무를 찾는게 이 문제가 요구하는것이다(해설참고함)

해결 DFS

is_cycle() 함수의 visited[] 값을 3가지로 정한게 참고한 답안. (이해하기가 쉽지 않았음.) 단순히 visited 체크된 값을 방문했을때 false를 해버리면 True도 false가 되어버린다(예시: TBD). 따라서 백트래킹으로 탐색할때, 이미 방문을 마친(이미 is_cycle() false 라서 사이클이 아님을 검증한) 노드는 2로 체크하여 굳이 다시 방문하지 않는다.

class Solution {
    vector<vector<int>> adj;
    bool is_cycle(vector<int> &vis, int cur) {
        /*
        vis 0: not visited
        vis 1: visited
        vis 2: no need to visit
        */
        if (vis[cur] == 1)
            return true;
        if (vis[cur] == 0) {
            vis[cur] = 1;
            for (int i = 0; i < adj[cur].size(); i++) {
                if (is_cycle(vis, adj[cur][i]))
                    return true;
            }
        }
        vis[cur] = 2;
        return false;
    }
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        adj = vector<vector<int>>(numCourses);
        vector<int> visites(numCourses, 0);
        
        for (auto it: prerequisites) {
            adj[it[1]].push_back(it[0]);
        }
        // 각 강좌들이 모두 연결되어있지 않을수도있기에, 모든 값을 순회한다.
        for (int i = 0; i < numCourses; i++) {
            if (is_cycle(visites, i))
                return false;
        }
        return true;
    }
};

해결 BFS

부모노드가 없는 노드 순서대로 BFS 탐색하면, 위상정렬된 순서가 나온다. 이것을 ret벡터에 저장하고, 만약 벡터의 크기가 주어진 강좌의 수와 다르다면 사이클이 존재한다는 의미.

class Solution {
    vector<vector<int>> adj;
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        adj = vector<vector<int>>(numCourses);
        unordered_map<int, int> indeg;
        vector<int> ret;
        // [1] -> [0]
        for (auto it: prerequisites) {
            adj[it[1]].push_back(it[0]);
            indeg[it[0]]++;
        }
        
        queue<int> q;
        for (int i = 0; i < numCourses; i++) {
            if (indeg[i] == 0)
                q.push(i);
        }
        while (!q.empty()) {
            int tgt = q.front();
            q.pop();
            ret.push_back(tgt);
            for (int i = 0; i < adj[tgt].size(); i++) {
                int adjval = adj[tgt][i];
                indeg[adjval]--;
                if (indeg[adjval] == 0)
                    q.push(adjval);
            }
        }
        if (ret.size() == numCourses)
            return true;
        return false;
    }
};

1791. Find Center of Star Graph

문제

1부터 n번호를 가진 노드 n개로 이루어진 무방향 그래프가 주어진다. 모든 노드와 연결되는 하나의 center노드가 존재하는데 이 노드를 찾아라.

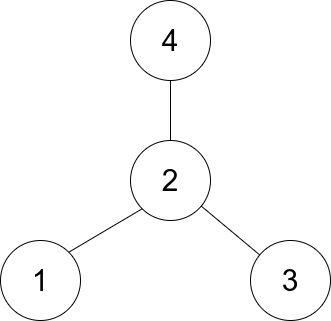
Input: edges = [[1,2],[2,3],[4,2]]
Output: 2
Explanation: As shown in the figure above, node 2 is connected to every other node, so 2 is the center.

해결

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        int esize = edges.size() + 2;
        vector<vector<int>> graph(esize);
        for (auto it: edges) {
            graph[it[0]].push_back(it[1]);
            graph[it[1]].push_back(it[0]);
        }
        for (int i = 1; i < esize; i++) {
            if (graph[i].size() > 1)
                return i;
        }
        return 0;
    }
};

1971. Find if Path Exists in Graph

문제

edge가 주어질때, source -> destination 에대한 경로가 존재하면 true 아니면 false.

Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2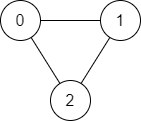

https://leetcode.com/problems/find-if-path-exists-in-graph/

해결 DFS - 그래프 인접행렬 방법

그래프 엣지를 표현하는 자료구조 생성(2차원배열로 graph map 생성)
이 방법은, 노드가 많은데 연결이 적은 그래프에서 2차원 배열사이즈가 과도하게 크고, 메모리를 많이 차지한다는 단점이있다.

제출해보면, 답은 맞는데 ,22/26 Test Case에서 Memory Limit Exceeded 가 발생.

int *visit;
int **map;
int dest;
int nr;

bool dfs(int **m, int row)
{
    if (row == dest)
        return true;
    if (visit[row])
        return false;
    visit[row] = 1;
    for (int i = 0; i < nr; i++) {
        if (m[row][i] == 1) {
            if (dfs(m, i))
                return true;
        }
    }
    return false;
}

bool validPath(int n, int** edges, int edgesSize, int* edgesColSize, int source, int destination)
{
    bool ret = false;
    dest = destination;
    nr = n;
    map = (int **)calloc(n, sizeof(int *));
    for (int i = 0; i < n; i++)
        map[i] = (int *)calloc(n, sizeof(int *));
    visit = (int *)calloc(n, sizeof(int));
    
    /* generate graph map */
    for (int i = 0; i < edgesSize; i++)
        map[edges[i][0]][edges[i][1]] = map[edges[i][1]][edges[i][0]] = 1;
    
    ret = dfs(map, source);
    for (int i = 0; i < n; i++)
        free(map[i]);
    free(map);
    return ret;
}

해결 DFS - 그래프 인접 리스트 방법

그래프 엣지를 표현하는 자료구조 생성(인접 리스트 방식) 가령, 엣지가 [[0,1],[0,2],[3,5],[5,4],[4,3]] 로 주어질때, 엣지를 표현하는 링크드 리스트는 아래와 같다.

[0] -> 1 -> 2
[1] -> 0
[2] -> 0
[3] -> 4 -> 5
[4] -> 3 -> 5
[5] -> 3 -> 4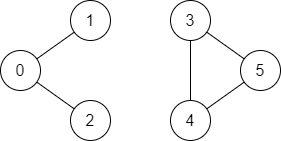

Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false

링크드 리스트를 생성할때 주의점. 이 그래프는 방향이 없는 그래프 이기 때문에, [a,b] 일때 a->b 그리고 b->a두개를 malloc해서 추가해야한다.

DFS구현은 visit[] 배열이 1로 바뀌느 시점 확인.

struct node {
    int val;
    struct node *next;
};
struct node **map;
bool *visit;

bool dfs(struct node **m, int curr, int dest)
{
    if (curr == dest)
        return true;
    if (visit[curr])
        return false;
    visit[curr] = 1;
    
    struct node *node = m[curr];
    for (;node != NULL; node = node->next)
        if (dfs(m, node->val, dest))
            return true;
    return false;
}

bool validPath(int n, int** edges, int edgesSize, int* edgesColSize, int source, int destination)
{
    map = (struct node **)calloc(n, sizeof(struct node *));
    visit = (bool *)calloc(n, sizeof(bool));
    
    /* generate graph map */
    for (int i = 0; i < edgesSize; i++) {
        // a -> b
        struct node *newnode = (struct node *)malloc(sizeof(struct node));
        newnode->val = edges[i][1];
        newnode->next = map[edges[i][0]];
        map[edges[i][0]] = newnode; 
        // b -> a
        newnode = (struct node *)malloc(sizeof(struct node));
        newnode->val = edges[i][0];
        newnode->next = map[edges[i][1]];
        map[edges[i][1]] = newnode; 
    }
    return dfs(map, source, destination);
}