Leetcode - 261. Graph Valid Tree

문제

주어진 그래프가 valid한 Tree인지 아닌지 판별하라

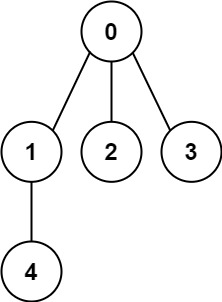
Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true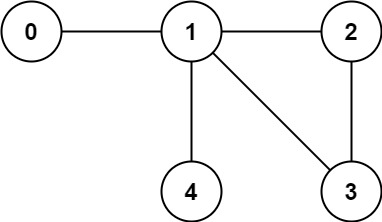

Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

해결 아이디어

• A valid Tree?

  • #1. All nodes are connected
  • #2. There are no cycles

• union-find를 사용하여 그래프에 cycle을 찾을 수 있고, 모든 노드의 대표노드가 같은지 파악하여 모든노드가 한 그룹인지 파악할 수 있다.

• loop detect방법
  [0,1], [1,2], [2,3] 의 그래프가 있다고 하자. 순서대로 union-find 를 수행하면 아래와 같다. 먼저 아직 union을 수행하지 않은채로 시작. 0번노드를 union() 수행하면 parent는 1이 된다. 1노드를 union() 수행하면 parent는 2가 된다. 다른 2노드의 union을 수행하면 parent는 find(0)을 통해 결국 2가 된다. 이 두값이 동일하므로 cycle이 존재한다. 따라서 연결하려는 두 링크의 대표노드가 서로 동일하면 Cycle이 존재하는것.

  노드	0	1	2
  parent	1	2	2

풀이

class Solution {
public:
    vector<int> parent;
    int find(int n) {
        if (parent[n] == n)
            return n;
        return find(parent[n]);
    }
    void do_union(int a, int b) {
        int roota = find(a);
        int rootb = find(b);
        parent[roota] = rootb;
    }
    bool validTree(int n, vector<vector<int>>& edges) {
        parent = vector<int>(n);
        for (int i = 0; i < n; i++)
            parent[i] = i;
        for (auto it: edges) {
            int root1 = find(it[0]);
            int root2 = find(it[1]);
            if (root1 == root2) // 연결하려는 두 링크의 대표노드가 동일하다면? -> Cycle존재
                return false;
            do_union(it[0], it[1]);
        }
        int prev = find(0);
        for (int i = 1; i < n; i++) {
            int next = find(i);
            if (prev != next) // represent node are not same == break rule #1
                return false;
            prev = next;
        }
        return true;
    }
};