Leetcode - 310. Minimum Height Trees

문제

0에서 n-1이름의 n개 노드로 구성된 무방향 그래프(Undirected Graph)가 주어진다. edges[] 는 각 노드의 엣지(간선)가 리스트업 되어있다. 어떤 노드도 루트노드가 될 수 있다고 할때, 트리의 높이가 가장 낮아지는 루트노드를 모두 구하라.

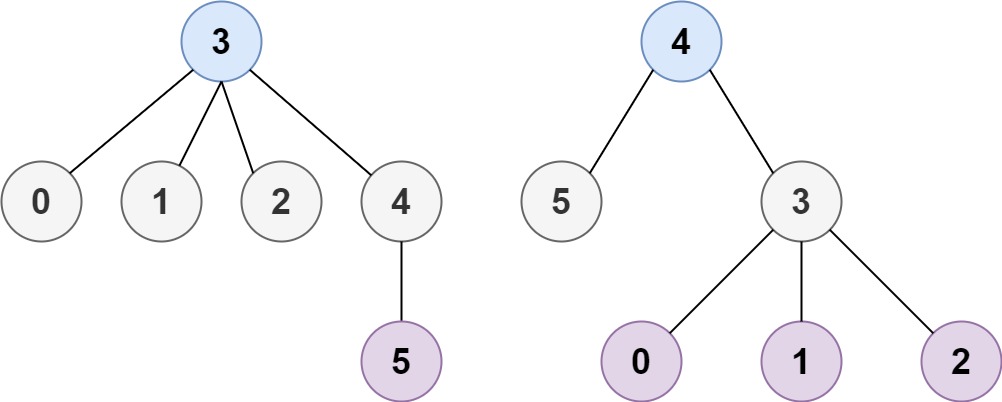
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

해결 아이디어

• Brute-force O(n^2) 문제 그대로 모든 노드에서부터 높이를 재서 가장 낮은 높이를 갖는 루트노드를 리턴.
  
• 2-DFS O(n) 아무노드에서 시작해 가장 멀리 떨어진 노드1를 찾는다. 그리고 그 노드부터 다시 가장 멀리 떨어진 노드2를 찾는다. 노드1 과 노드 2가 해당 그래프에서 가장 멀리 떨어진 노드가 된다. 여기서 중간의 노드 (1개 혹은 2개)를 리턴하면 된다.
  
• Topology Sort 방법 O(n) The basic idea is "keep deleting leaves layer-by-layer, until reach the root." 간선 갯수가 1개인 노드부터 단계별로 제거한다. 그러다보면 마지막 까지 남는 노드가 생기는데, 그 노드가 결과값이된다. 이를 위해 Topology Sort 를 사용하면 된다. 이전까지는 방향이 있는 그래프에서 사용했는데 그때는 배열하나에 진입차수 갯수를 저장했다면, 무방향 그래프에서는 노드에 연결된 간선 갯수자체를 저장한다. 간선 갯수가 1개인 노드가 바로 가장 마지막 layer의 노드가 된다. 이 layer별로 q에 삽입후 제거하는 방식으로 동작한다.
  

풀이1 - Brute-force O(n^2)

class Solution {
public:
    vector<vector<int>> graph;
    
    int get_hight_from(int root, vector<bool> &visit) {
        vector<int> depth(visit.size());
        queue<int> q;
        q.push(root);
        int curr = 0;
        
        while (!q.empty()) {
            curr = q.front();
            q.pop();
            visit[curr] = true;
            for (int i = 0; i < graph[curr].size(); i++) {
                if (visit[graph[curr][i]] == true)
                    continue;
                q.push(graph[curr][i]);
                depth[graph[curr][i]] = depth[curr] + 1;
            }
        }
        return depth[curr];
    }
        
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        vector<int> ret;
        vector<int> hight(n);
        int min_hight = n + 1;
        
        graph = vector<vector<int>>(n);
        for (auto it: edges) {
            graph[it[0]].push_back(it[1]);
            graph[it[1]].push_back(it[0]);
        }
        /*
        with edges [[3,0],[3,1],[3,2],[3,4],[5,4]], the graph will be:
        0 -> 3
        1 -> 3
        2 -> 3
        3 -> 0 -> 1 -> 2 -> 4
        4 -> 3 -> 5
        */
        
        for (int i = 0; i < n; i++) {
            vector<bool> visit(n, false);
            hight[i] = get_hight_from(i, visit);
            min_hight = std::min(hight[i], min_hight);
        }
        for (int i = 0; i < n; i++) {
            if (hight[i] == min_hight)
                ret.push_back(i);
        }
        return ret;
    }
};

풀이2 - 2-DFS방법 O(n)

class Solution {
public:
    vector<vector<int>> graph;
    int max_depth = 0;
    vector<int> longest_path;
    vector<int> tmp;
    
    void get_longest(int node, int depth, vector<bool> &visit) {
        if (visit[node] == true)
            return;
        tmp.push_back(node);
        if (depth > max_depth) {
            longest_path = tmp;
            max_depth = depth;
        }
        
        for (int i = 0; i < graph[node].size(); i++) {
            visit[node] = true;
            get_longest(graph[node][i], depth + 1, visit);
        }
        tmp.pop_back();
        
    }
        
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        if (n == 1)
            return {0};
        graph = vector<vector<int>>(n);
        for (auto it: edges) {
            graph[it[0]].push_back(it[1]);
            graph[it[1]].push_back(it[0]);
        }

        
        /* 1st dfs */
        max_depth = 0;
        vector<bool> visit(edges.size(), false);
        get_longest(0, 0, visit);
        int first_node = longest_path[max_depth];
        
        /* 2st dfs */
        max_depth = 0;
        visit = vector<bool>(edges.size(), false);
        get_longest(first_node, 0, visit);
        int second_node = longest_path[max_depth];
        
        /* if max_depth is odd, the number of node in longest path is even
             0 1 [2 3] 4 5
           else:
             0 1 [2] 3 4
        */
        int mid = max_depth / 2;
        if (max_depth % 2 == 1)
            return {longest_path[mid], longest_path[mid + 1]};
        return {longest_path[mid]};
    }
};

풀이3 - Topology Sort 방법 O(n)

class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        vector<vector<int>> graph(n);
        unordered_map<int, int> indeg;
        queue<int> q;
        
        if (n == 1)
            return {0};

        /* generate graph data structure */
        for (auto it: edges) {
            graph[it[0]].push_back(it[1]);
            graph[it[1]].push_back(it[0]);
            indeg[it[0]]++;
            indeg[it[1]]++;
        }
        /* push the nodes which is indegree 1 */
        for (auto it: indeg) {
            if (it.second == 1) {
                q.push(it.first);
            }
        }
        
        /* bfs - topology sort  */
        vector<int> ret;
        while (!q.empty()) {
            int nr_leaves = q.size(); // number of leaf nodes current steps.
            ret.clear(); // 
            while (nr_leaves--) { 
                int node = q.front();
                q.pop();
                indeg[node]--;
                ret.push_back(node); // so every step, leaf node will be added in ret. 

                for (int i = 0; i < graph[node].size(); i++) {
                    int adj = graph[node][i];
                    indeg[adj]--;
                    if (indeg[adj] == 1) // the adjacent node is become a leaf
                        q.push(adj); // a new leaf node is added 
                }
            }
        }
        return ret;
    }
};