Algorithm - Backtracking Problems

Programmers Problem : N-Queen

• 가로, 세로 길이가 n인 정사각형으로된 체스판이 있습니다. 체스판 위의 n개의 퀸이 서로를 공격할 수 없도록 배치하고 싶습니다.

• 예를 들어서 n이 4인 경우, 다음과 같이 퀸을 배치하면 n개의 퀸은 서로를 한번에 공격 할 수 없습니다.

• 체스판의 가로 세로의 세로의 길이 n이 매개변수로 주어질 때, n개의 퀸이 조건에 만족 하도록 배치할 수 있는 방법의 수를 return하는 solution함수를 완성해주세요.

• 제한사항

  • 퀸(Queen)은 가로, 세로, 대각선으로 이동할 수 있습니다.
  • n은 12이하의 자연수 입니다.

Solution

function solution(n) {
    let answer = 0;
    
    const backtracking = (board, rowIndex) => {
        if(rowIndex === n) {
            answer++;
            return;
        }
        
        const nextRowIndex = rowIndex + 1;
        for(let i = 1; i <= n; i++) {
            board[nextRowIndex] = i;
            if(isPromising(board,nextRowIndex)) {
                backtracking(board, nextRowIndex);
            }
        }
  }
  
  const isPromising = (board, rowIndex) => {
    for(let i = 1; i < rowIndex; i++) {
      if(board[i] === board[rowIndex]) {
          return false;
      }
      if(Math.abs(board[i] - board[rowIndex]) === rowIndex - i) {
          return false;
      }
    }
    return true;
  }
  
  for(let i = 1; i <= n; i++) {
    const board = new Array(n+1).fill(0);
    board[1] = i;
    backtracking(board, 1);
  }
  
  return answer;
}

LeetCode Problem : N-Queens

• The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

• Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

• Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

• Example:

  • Input: n = 4
  • Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
  • Explanation: There exist two distinct solutions to the 4-queens puzzle as shown below

Solution

/**
 * @param {number} n
 * @return {string[][]}
 */
var solveNQueens = function(n) {
    const casesOfChessboard = [];

    const backtracking = (board, rowIndex, colPlacements) => {
        if(rowIndex === n) {
            const chessboard = colPlacements.map(queenIndex => {
                const queenStrIndex = queenIndex - 1;
                return '.'.repeat(queenStrIndex) + 'Q' + '.'.repeat(n - queenStrIndex - 1);
            });
            casesOfChessboard.push(chessboard);
            return;
        }
        
        const nextRowIndex = rowIndex + 1;
        for(let i = 1; i <= n; i++) {
            board[nextRowIndex] = i;
            colPlacements.push(i);
            if(isPromising(board,nextRowIndex)) {
                backtracking(board, nextRowIndex, colPlacements);
            }
            colPlacements.pop();
        }
    };
    
    const isPromising = (board, rowIndex) => {
        for(let i = 1; i < rowIndex; i++) {
            if(board[i] === board[rowIndex]) {
                return false;
            }
        if(Math.abs(board[i] - board[rowIndex]) === rowIndex - i) {
            return false;
        }
    }
    return true;
    };
    
    for(let i = 1; i <= n; i++) {
        const board = new Array(n+1).fill(0);
        const colPlacements = [];
        board[1] = i;
        colPlacements.push(i);
        backtracking(board, 1, colPlacements);
    }
    
    return casesOfChessboard;
};

LeetCode Problem : Beautiful Arrangement

• Suppose you have n integers labeled 1 through n. A permutation of those n integers perm (1-indexed) is considered a beautiful arrangement if for every i (1 <= i <= n), either of the following is true:

  • perm[i] is divisible by i.
  • i is divisible by perm[i].

• Given an integer n, return the number of the beautiful arrangements that you can construct.

• Example 1:

  • Input: n = 2
  • Output: 2
  • Explanation:
    • The first beautiful arrangement is [1,2]:
      • perm[1] = 1 is divisible by i = 1
      • perm[2] = 2 is divisible by i = 2
    • The second beautiful arrangement is [2,1]:
      • perm[1] = 2 is divisible by i = 1
      • i = 2 is divisible by perm[2] = 1

Solution

/**
 * @param {number} n
 * @return {number}
 */
var countArrangement = function(n) {
    let count = 0;
    const visited = new Array(n+1).fill(false);

    const backtracking = (num) => {
        if (num > n) {
            count++;
            return;
        }

        for (let index = 1; index <= n; index++) {
            if (!visited[index] && (index % num === 0 || num % index === 0)) {
                visited[index] = true;
                backtracking(num+1);
                visited[index] = false;
            }
        }
    } 

    backtracking(1);
    return count;
};

LeetCode Problem : Binary Tree Paths

• Given the root of a binary tree, return all root-to-leaf paths in any order .

  • A leaf is a node with no children.

• Example 1:

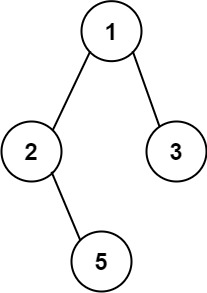
  • Input: root = [1,2,3,null,5]
  • Output: ["1->2->5","1->3"]

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {string[]}
 */
var binaryTreePaths = function(root) {
    const paths = [];
    
    const dfs = (node, curPath) => {
        if (!node) {
            return;
        }
        if (!node.left && !node.right) {
            const totalPath = [...curPath, node.val].join('->');
            paths.push(totalPath);
            return;
        }
        dfs(node.left, [...curPath, node.val]);
        dfs(node.right, [...curPath, node.val]);
    }

    dfs(root, []);
    
    return paths;
};

LeetCode Problem : Unique Paths 3

• You are given an m x n integer array grid where grid[i][j] could be:
  • 1 representing the starting square. There is exactly one starting square.
  • 2 representing the ending square. There is exactly one ending square.
  • 0 representing empty squares we can walk over.
  • -1 representing obstacles that we cannot walk over.
• Return the number of 4-directional walks from the starting square to the ending square, that walk over every non-obstacle square exactly once.

• Example 1:

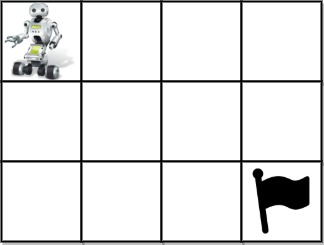
  • Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,2,-1]]

  • Output: 2

  • Explanation: We have the following two paths:

    1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
    2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

• Example 2:
  • Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,2]]
  • Output: 4
  • Explanation: We have the following four paths:
    1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
    2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
    3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
    4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

Solution

/**
 * @param {number[][]} grid
 * @return {number}
 */
var uniquePathsIII = function(grid) {
    let count = 0;
    const rowLength = grid.length;
    const colLength = grid[0].length;
    const movement = [[0,1], [1,0], [0, -1], [-1, 0]];
    let walkable = rowLength * colLength;
    let start, end;

    for (let r = 0; r < rowLength; r++) {
        for (let c = 0; c < colLength; c++) {
            if (grid[r][c] === 1) {
                start = [r, c];
                continue;
            }
            if (grid[r][c] === 2) {
                end = [r, c];
                continue;
            }
            if (grid[r][c] === -1) {
                walkable--;
            }
        }
    }

    const dfs = (i, j, walked) => {
        for (const [dr, dc] of movement) {
            const row = i + dr, col = j + dc;
            if (row < 0 || row >= rowLength || col < 0 || col >= colLength || grid[row][col] === 1 ||grid[row][col] === -1) {
                continue;
            }

            if (row === end[0] && col === end[1]) {
                if (walked + 1 === walkable) {
                    count++;
                    continue;
                }
            }

            grid[row][col] = 1;
            dfs(row, col, walked + 1);
            grid[row][col] = 0;
        }
    };

    dfs(start[0], start[1], 1);
    return count;
};

LeetCode Problem : Generate Parentheses

• Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

Example

• Input: n = 3
• Output: ["((()))","(()())","(())()","()(())","()()()"]

Constraints

• 1 <= n <= 8

Solution

/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function(n) {
    const result = [];
    const backTracking = (str, open, close) => {
        if (open === n && close === n) {
            result.push(str);
            return;
        }

        if (open < n) {
            backTracking(str + '(', open + 1, close);
        }
        if (open > close) {
            backTracking(str + ')', open, close + 1);
        }
    };

    backTracking('', 0, 0);
    return result;
};

LeetCode : Letter Tile Possibilities

• You have n tiles, where each tile has one letter tiles[i] printed on it.

Return the number of possible non-empty sequences of letters you can make using the letters printed on those tiles.

Example

• Input: tiles = "AAB"
• Output: 8
• Explanation: The possible sequences are "A", "B", "AA", "AB", "BA", "AAB", "ABA", "BAA".

Constraints

• 1 <= tiles.length <= 7
• tiles consists of uppercase English letters.

Solution

/**
 * @param {string} tiles
 * @return {number}
 */
var numTilePossibilities = function(tiles) {
    const sequenceSet = new Set();

    const dfs = (tiles, str) => {
        if (!tiles.length) {
            return;
        }

        for (let i = 0; i < tiles.length; i++) {
            str.push(tiles[i]);
            sequenceSet.add(str.join(''));
            rest = tiles.filter((_, index) => index !== i);
            dfs(rest,str);
            str.pop();

        }
    };

    dfs(tiles.split(''), []);
    
    return sequenceSet.size;
};