Algorithm - DP Problems

이소라·2022년 11월 2일

Algorithm

목록 보기

29/77

LeetCode Problem : N-th Tribonacci Number

The Tribonacci sequence Tn is defined as follows:
- T0 = 0, T1 = 1, T2 = 1, and Tn+3 = Tn + Tn+1 + Tn+2 for n >= 0.
Given n, return the value of Tn
- Constraints:
  - 0 <= n <= 37
  - The answer is guaranteed to fit within a 32-bit integer, ie. answer <= 2^31 - 1.
Example 1:
- Input: n = 4
- Output: 4
- Explanation:
  - T_3 = 0 + 1 + 1 = 2
  - T_4 = 1 + 1 + 2 = 4

Solution

/**
 * @param {number} n
 * @return {number}
 */
var tribonacci = function(n, memo = []) {
    if (memo[n]) return memo[n];
    if (n === 0) return 0;
    if (n === 1 || n === 2) return 1;
    const thirdNumber = tribonacci(n - 1, memo) + tribonacci(n - 2, memo) + tribonacci(n - 3, memo)
    memo[n] = thirdNumber;
    return thirdNumber;
};

LeetCode Problem : Min Cost Climbing Stairs

You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps.
You can either start from the step with index 0, or the step with index 1.
Return the minimum cost to reach the top of the floor.
- Constraints:
  - 2 <= cost.length <= 1000
  - 0 <= cost[i] <= 999
Example 1:
- Input: cost = [10,15,20]
- Output: 15
- Explanation:
  - You will start at index 1.
    - Pay 15 and climb two steps to reach the top.
  - The total cost is 15.
Example 2:
- Input: cost = [1,100,1,1,1,100,1,1,100,1]
- Output: 6
- Explanation:
  - You will start at index 0.
  - Pay 1 and climb two steps to reach index 2.
  - Pay 1 and climb two steps to reach index 4.
  - Pay 1 and climb two steps to reach index 6.
  - Pay 1 and climb one step to reach index 7.
  - Pay 1 and climb two steps to reach index 9.
  - Pay 1 and climb one step to reach the top.
  - The total cost is 6.

Solution

/**
 * @param {number[]} cost
 * @return {number}
 */
var minCostClimbingStairs = function(cost) {
    const length = cost.length;
    const memo = [];
    
    function dp(cost, index) {
        if (index < 0) return 0;
        if (index === 0 || index === 1) return cost[index];
        if (memo[index]) return memo[index];
        memo[index] = cost[index] + Math.min(dp(cost, index - 1), dp(cost, index -2));
        return memo[index];
    }
    
    return Math.min(dp(cost, length - 1), dp(cost, length - 2));
};

LeetCode Problem : Pascal's Triangle II

Given an integer rowIndex, return the rowIndexth (0-indexed) row of the Pascal's triangle.
In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:
- Constraints:
- 0 <= rowIndex <= 33

Solution

/**
 * @param {number} rowIndex
 * @return {number[]}
 */
var getRow = function(rowIndex) {
    if (!rowIndex) return [1];
    
    let memo = [1, 1];
    let currRow;
    
    while(--rowIndex) {
        currRow = [1];
        for (let i = 0; i < memo.length - 1; i++) {
            currRow.push(memo[i] + memo[i + 1]);
        }
        
        currRow.push(1);
        memo = currRow;
    }
    
    
    return memo;
};

LeetCode Problem : Best Time to Buy and Sell Stock

You are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
- Constraints:
  - 1 <= prices.length <= 10^5
  - 0 <= prices[i] <= 10^4
Example 1:
- Input: prices = [7,1,5,3,6,4]
- Output: 5
- Explanation:
  - Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
  - Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
Example 2 :
- Input: prices = [7,6,4,3,1]
- Output: 0
- Explanation:
  - In this case, no transactions are done and the max profit = 0.

Solution

/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(prices) {
    const length = prices.length;
    let profit = 0;
    let buyPrice = Infinity;
    let sellPrice;
    
    for (let i = 0; i < length - 1; i++) {
        if (prices[i] > buyPrice) continue;
        buyPrice = prices[i];
        
        for (let j = i + 1; j < length; j++) {
            sellPrice = prices[j];
            if (sellPrice <= buyPrice) continue;
            if (sellPrice - buyPrice > profit) {
                profit = sellPrice - buyPrice;
            }
        }
    }
    
    return profit;
};

LeetCode Problem : Climbing Stairs

You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Constraints:
- 1 <= n <= 45
Example 1:
- Input: n = 2
- Output: 2
- Explanation:
  1. 1 step + 1 step
  2. 2 steps
Example 2:
- Input: n = 3
- Output: 3
- Explanation:
  1. 1 step + 1 step + 1 step
  2. 1 step + 2 steps
  3. 2 steps + 1 step

Solution

/**
 * @param {number} n
 * @return {number}
 */
var climbStairs = function(n) {
    let stairs = new Array(n+1).fill(0);
    stairs[1] = 1;
    stairs[2] = 2;

    for (let i = 3; i <= n; i++) {
        stairs[i] = stairs[i - 1] + stairs[i - 2];
    }
    return stairs[n];
};

// 2 ~ 7의 계단 오르는 방법 경우의 수
2 : 1 + 1 = 2
3 : 1 + 2 = 3
4 : 1 + 3 + 1 = 5
5 : 1 + 4 + 3(2+1) = 8
6 : 1 + 5 + 6(3+2+1) + 1 = 13
7 : 1 + 6 + 10(4+3+2+1) + 4 = 21

규칙 파악하기
- 점화식 : dp[n] = dp[n - 1] + dp[n - 2]

LeetCode Problem : Count Square Submatrices with All Ones

Given a m * n matrix of ones and zeros, return how many square submatrices have all ones.

Examples

Example 1
- Input: matrix = [[0,1,1,1], [1,1,1,1], [0,1,1,1]]
- Output: 15
- Explanation:
  - There are 10 squares of side 1.
  - There are 4 squares of side 2.
  - There is 1 square of side 3.
  - Total number of squares = 10 + 4 + 1 = 15.
Example 2
- Input: matrix = [[1,0,1], [1,1,0], [1,1,0]]
- Output: 7
- Explanation:
  - There are 6 squares of side 1.
  - There is 1 square of side 2.
  - Total number of squares = 6 + 1 = 7.

Constraints

1 <= arr.length <= 300
1 <= arr[0].length <= 300
0 <= arr[i][j] <= 1

Solution

다른 사람 문제 풀이 참고(Python/JS/C++ O(m*n) sol by DP)
- 각 배열 요소에 대한 정사각형의 최대 길이를 구하는 문제
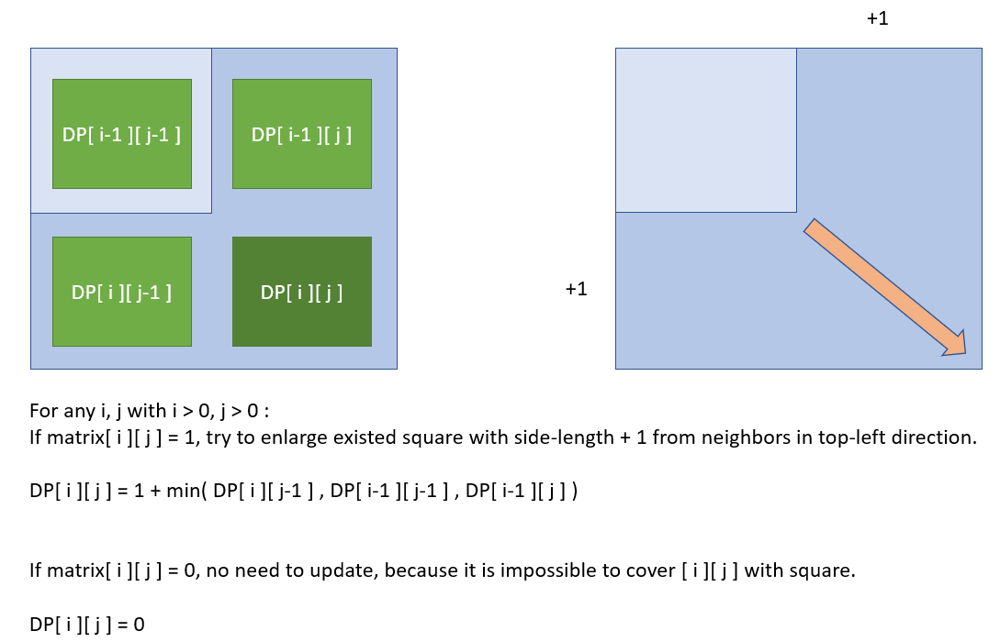
- i행, j열 요소에 대한 정사각형의 최대 길이를 DP[i][j]라고할 때,
  - i행, j열의 요소가 1일 경우,
  - DP[i][j] = 1 + Math.min(DP[i-1][j-1], DP[i-1][j], DP[i][j-1])

DP Table

1	1	1
1	1	2
1	2	2
1	2	3

total counts of squares = 1 + 1 + 1 + 1 + 2 + 2 + 1 + 2 + 3 = 14

/**
 * @param {number[][]} matrix
 * @return {number}
 */
var countSquares = function(matrix) {
    let result = 0;

    for (let i = 0; i < matrix.length; i++) {
        for (let j = 0; j < matrix[0].length; j++) {
            if (!matrix[i][j]) {
                continue;
            }

            if (i > 0 && j > 0) {
                matrix[i][j] = 1 + Math.min(matrix[i - 1][j - 1], matrix[i - 1][j], matrix[i][j - 1]);
            }

            result += matrix[i][j];
        }
    }
    return result;
};