Algorithm - LeetCode Problems 14

Problem 1678. Goal Parser Interpretation

• You own a Goal Parser that can interpret a string command. The command consists of an alphabet of "G", "()" and/or "(al)" in some order. The Goal Parser will interpret "G" as the string "G", "()" as the string "o", and "(al)" as the string "al". The interpreted strings are then concatenated in the original order.

• Given the string command, return the Goal Parser's interpretation of command.

Examples

• Example 1:

  • Input: command = "G()(al)"
  • Output: "Goal"
  • Explanation: The Goal Parser interprets the command as follows:
    • G -> G
    • () -> o
    • (al) -> al
    • The final concatenated result is "Goal".

• Example 2:

  • Input: command = "G()()()()(al)"
  • Output: "Gooooal"

• Example 3:

  • Input: command = "(al)G(al)()()G"
  • Output: "alGalooG"

Constraints

• 1 <= command.length <= 100
• command consists of "G", "()", and/or "(al)" in some order.

Solution

• for 문, join 메서드를 사용한 풀이

/**
 * @param {string} command
 * @return {string}
 */
var interpret = function(command) {
    const strArr = [];
    let str = '';

    for (const letter of command) {
        if (letter === 'G') {
            strArr.push(letter);
            str = '';
        } else if (letter === '(') {
            str = letter;
        } else if (letter === ')') {
            str += letter;
            str = str.length > 2 ? 'al' : 'o';
            strArr.push(str);
            str = '';
        } else {
            str += letter;
        }
    }
    
    return strArr.join('');
};

• split, join 메서드를 사용한 풀이

/**
 * @param {string} command
 * @return {string}
 */
var interpret = function(command) {
    return command.split('()').join('o').split('(al)').join('al');
};

Problem 1020. Number of Enclaves

• You are given an m x n binary matrix grid, where 0 represents a sea cell and 1 represents a land cell.

• A move consists of walking from one land cell to another adjacent (4-directionally) land cell or walking off the boundary of the grid.

• Return the number of land cells in grid for which we cannot walk off the boundary of the grid in any number of moves.

Examples

• Example 1:
  • Input: grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
  • Output: 3
  • Explanation: There are three 1s that are enclosed by 0s, and one 1 that is not enclosed because its on the boundary.

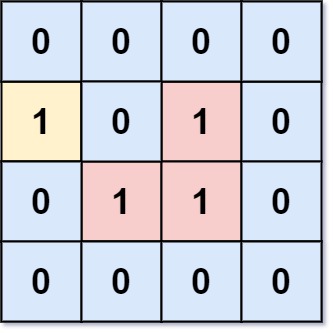
• Example 2:
  • Input: grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
  • Output: 0
  • Explanation: All 1s are either on the boundary or can reach the boundary.

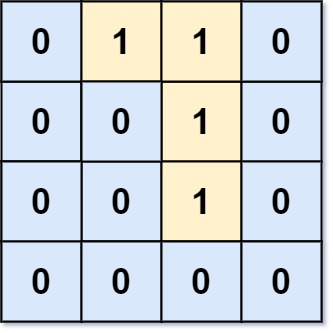
Constraints

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 500
• grid[i][j] is either 0 or 1.

Solution

/**
 * @param {number[][]} grid
 * @return {number}
 */
var numEnclaves = function(grid) {
    const M = grid.length;
    const N = grid[0].length;
    const directions = [[-1, 0], [1, 0], [0, -1], [0, 1]];

    const dfs = (x, y) => {
        grid[x][y] = 0;

        for (const [dx, dy] of directions) {
            const nx = x + dx;
            const ny = y + dy;
            if (nx >= 0 && nx < M && ny >= 0 && ny < N && grid[nx][ny]) {
                dfs(nx, ny);
            }
        }
    }

    for (let i = 0; i < M; i++) {
        if (grid[i][0]) {
            dfs(i, 0);
        }
        if (grid[i][N - 1]) {
            dfs(i, N - 1);
        }
    }

    for (let j = 0; j < N; j++) {
        if (grid[0][j]) {
            dfs(0, j);
        }
        if (grid[M - 1][j]) {
            dfs(M - 1, j);
        }
    }
    
    let landCount = 0;
    for (let i = 0; i < M; i++) {
        for (let j = 0; j < N; j++) {
            if (grid[i][j]) {
                landCount++;
            }
        }
    }
    
    return landCount;
};

Problem 1021. Remove Outermost Parentheses

• A valid parentheses string is either empty "", "(" + A + ")", or A + B, where A and B are valid parentheses strings, and + represents string concatenation.

  • For example, "", "()", "(())()", and "(()(()))" are all valid parentheses strings.

• A valid parentheses string s is primitive if it is nonempty, and there does not exist a way to split it into s = A + B, with A and B nonempty valid parentheses strings.

• Given a valid parentheses string s, consider its primitive decomposition: s = P1 + P2 + ... + Pk, where Pi are primitive valid parentheses strings.

• Return s after removing the outermost parentheses of every primitive string in the primitive decomposition of s.

Examples

• Example 1:

  • Input: s = "(()())(())"
  • Output: "()()()"
  • Explanation:
    • The input string is "(()())(())", with primitive decomposition "(()())" + "(())".
    • After removing outer parentheses of each part, this is "()()" + "()" = "()()()".

• Example 2:

  • Input: s = "(()())(())(()(()))"
  • Output: "()()()()(())"
  • Explanation:
    • The input string is "(()())(())(()(()))", with primitive decomposition "(()())" + "(())" + "(()(()))".
    • After removing outer parentheses of each part, this is "()()" + "()" + "()(())" = "()()()()(())".

• Example 3:

  • Input: s = "()()"
  • Output: ""
  • Explanation:
    • The input string is "()()", with primitive decomposition "()" + "()".
    • After removing outer parentheses of each part, this is "" + "" = "".

Constraints

• 1 <= s.length <= 10^5
• s[i] is either '(' or ')'.
• s is a valid parentheses string.

Solution

/**
 * @param {string} s
 * @return {string}
 */
var removeOuterParentheses = function(s) {
    const stack = [];
    let openParenthesisCount = 0;
    let closeParenthesisCount = 0;
    let validParenthesis = '';

    for (const letter of s) {
        if (letter === '(') {
            openParenthesisCount++;
        }
        if (letter === ')') {
            closeParenthesisCount++;
        }
        if (openParenthesisCount === closeParenthesisCount) {
            if (validParenthesis.length) {
                stack.push(validParenthesis);
            }
            validParenthesis = '';
            openParenthesisCount = 0;
            closeParenthesisCount = 0;
        } else {
            if (openParenthesisCount > 1) {
                validParenthesis += letter;
            }
        }
    }
    return stack.join('');
};