Algorithm - LeetCode Problems 17

Problem 1043. Partition Array for Maximum Sum

• Given an integer array arr, partition the array into (contiguous) subarrays of length at most k. After partitioning, each subarray has their values changed to become the maximum value of that subarray.

• Return the largest sum of the given array after partitioning. Test cases are generated so that the answer fits in a 32-bit integer.

Examples

• Example 1:

  • Input: arr = [1,15,7,9,2,5,10], k = 3
  • Output: 84
  • Explanation: arr becomes [15,15,15,9,10,10,10]

• Example 2:

  • Input: arr = [1,4,1,5,7,3,6,1,9,9,3], k = 4
  • Output: 83

• Example 3:

  • Input: arr = [1], k = 1
  • Output: 1

Constraints:

• 1 <= arr.length <= 500
• 0 <= arr[i] <= 10^9
• 1 <= k <= arr.length

Solution

• 다른 사람 풀이 참고 (Better indexing than the highest voted answer)

/**
 * @param {number[]} arr
 * @param {number} k
 * @return {number}
 */
var maxSumAfterPartitioning = function(arr, k) {
    const totalLength = arr.length;
    const dp = new Array(totalLength + 1);

    let sum = 0;
    for (let i = 0; i <= totalLength; i++) {
        dp[i] = sum;
        sum += arr[i];
    }

    for (let i = 0; i <= totalLength; i++) {
        let maxSum = 0;
        for (let j = 1; j <= k && j <= i; j++) {
            maxSum = Math.max(maxSum, arr[i - j]);
            dp[i] = Math.max(dp[i], dp[i - j] + maxSum * j);
        }
    }

    return dp[totalLength];
};

Problem 1827. Minimum Operations to Make the Array Increasing

You are given an integer array nums (0-indexed). In one operation, you can choose an element of the array and increment it by 1.

For example, if nums = [1,2,3], you can choose to increment nums[1] to make nums = [1,3,3].
Return the minimum number of operations needed to make nums strictly increasing.

An array nums is strictly increasing if nums[i] < nums[i+1] for all 0 <= i < nums.length - 1. An array of length 1 is trivially strictly increasing.

Examples

• Example 1:

  • Input: nums = [1,1,1]
  • Output: 3
  • Explanation: You can do the following operations:
    1. Increment nums[2], so nums becomes [1,1,2].
    2. Increment nums[1], so nums becomes [1,2,2].
    3. Increment nums[2], so nums becomes [1,2,3].

• Example 2:

  • Input: nums = [1,5,2,4,1]
  • Output: 14

• Example 3:

  • Input: nums = [8]
  • Output: 0

Constraints:

• 1 <= nums.length <= 5000
• 1 <= nums[i] <= 10^4

Solution

/**
 * @param {number[]} nums
 * @return {number}
 */
var minOperations = function(nums) {
    if (nums.length < 2) {
        return 0;
    }
    let operationCount = 0;
    for (let i = 1; i < nums.length; i++) {
        if (nums[i] <= nums[i - 1]) {
            const change = nums[i - 1] - nums[i] + 1;
            operationCount += change;
            nums[i] += change;
        }
    }

    return operationCount;
};

Problem 1254. Number of Closed Islands

• Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

• Return the number of closed islands.

Examples

• Example 1:
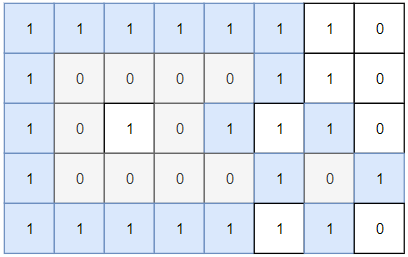
  • Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
  • Output: 2
  • Explanation:
    • Islands in gray are closed because they are completely surrounded by water (group of 1s).

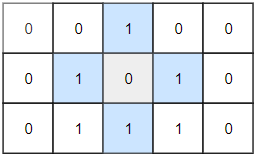
• Example 2:
• Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
• Output: 1

Constraints

• 1 <= grid.length, grid[0].length <= 100
• 0 <= grid[i][j] <=1

Solution

/**
 * @param {number[][]} grid
 * @return {number}
 */
var closedIsland = function(grid) {
    const rowLength = grid.length;
    const colLength = grid[0].length;
    const directions = [[1, 0], [-1, 0], [0, 1], [0, -1]];
    let closedIslandCount = 0;

    const isOutsideGrid = (row, col) => {
        return  row < 0 || row >= rowLength || col < 0 || col >= colLength;
    };

    const isClosedIsland = (row, col) => {
        const queue = [[row, col]];
        let isClosed = true;
        grid[row][col] = true;

        while (queue.length) {
            const [x, y] = queue.shift();
            for (const [dx, dy] of directions) {
                const nx = x + dx;
                const ny = y + dy;

                if (isOutsideGrid(nx, ny)) {
                    isClosed = false;
                } else if (!grid[nx][ny]) {
                    grid[nx][ny] = true;
                    queue.push([nx, ny]);
                }
            }
        }
        return isClosed;
    };

    for (let row = 0; row < rowLength; row++) {
        for (let col = 0; col < colLength; col++) {
            if (!grid[row][col] && isClosedIsland(row, col)) {
                closedIslandCount++;
            }
        }
    }

    return closedIslandCount;
};

Problem 1525. Number of Good Ways to Split a String

• You are given a string s.

• A split is called good if you can split s into two non-empty strings sleft and sright where their concatenation is equal to s (i.e., sleft + sright = s) and the number of distinct letters in sleft and sright is the same.

• Return the number of good splits you can make in s.

Examples

• Example 1:

  • Input: s = "aacaba"
  • Output: 2
  • Explanation: There are 5 ways to split "aacaba" and 2 of them are good.
    • ("a", "acaba") Left string and right string contains 1 and 3 different letters respectively.
    • ("aa", "caba") Left string and right string contains 1 and 3 different letters respectively.
    • ("aac", "aba") Left string and right string contains 2 and 2 different letters respectively (good split).
    • ("aaca", "ba") Left string and right string contains 2 and 2 different letters respectively (good split).
    • ("aacab", "a") Left string and right string contains 3 and 1 different letters respectively.

• Example 2:

  • Input: s = "abcd"
  • Output: 1
  • Explanation: Split the string as follows ("ab", "cd").

Constraints

• 1 <= s.length <= 10*5
• s consists of only lowercase English letters.

Solution

• 시간 초과된 풀이

/**
 * @param {string} s
 * @return {number}
 */
var numSplits = function(s) {
    let goodSplitCount = 0;
    
    for (let i = 1; i < s.length; i++) {
        const leftSetSize = new Set(s.substring(0, i)).size;
        const rightSetSize = new Set(s.substring(i)).size;
        if (leftSetSize === rightSetSize) {
            goodSplitCount++;
        }
    }

    return goodSplitCount;
};

• 2개의 Set과 1개의 array를 사용한 풀이

/**
 * @param {string} s
 * @return {number}
 */
var numSplits = function(s) {
    const totalLength = s.length;
    const leftSet = new Set();
    const rightSet = new Set();
    const leftSetSizes = [];
    let goodSplitCount = 0;

    for (let i = 0; i < totalLength; i++) {
        leftSet.add(s[i]);
        leftSetSizes[i] = leftSet.size;
    }

    for (let j = totalLength - 1; j > 0; j--) {
        rightSet.add(s[j]);
        if (leftSetSizes[j - 1] === rightSet.size) {
            goodSplitCount++;
        }
    }

    return goodSplitCount;
};