Algorithm - Programmers & LeetCode Problems 7

이소라·2023년 12월 11일

Algorithm

목록 보기

71/77

LeetCode Problem 2149. Rearrange Array Elements by Sign

You are given a 0-indexed integer array nums of even length consisting of an equal number of positive and negative integers.
You should rearrange the elements of nums such that the modified array follows the given conditions:
Every consecutive pair of integers have opposite signs.
For all integers with the same sign, the order in which they were present in nums is preserved.
The rearranged array begins with a positive integer.
Return the modified array after rearranging the elements to satisfy the aforementioned conditions.

Examples

Example 1:
- Input: nums = [3,1,-2,-5,2,-4]
- Output: [3,-2,1,-5,2,-4]
- Explanation:
  - The positive integers in nums are [3,1,2]. The negative integers are [-2,-5,-4].
  - The only possible way to rearrange them such that they satisfy all conditions is [3,-2,1,-5,2,-4].
  - Other ways such as [1,-2,2,-5,3,-4], [3,1,2,-2,-5,-4], [-2,3,-5,1,-4,2] are incorrect because they do not satisfy one or more conditions.
Example 2:
- Input: nums = [-1,1]
- Output: [1,-1]
- Explanation:
  - 1 is the only positive integer and -1 the only negative integer in nums.
  - So nums is rearranged to [1,-1].

Constraints

2 <= nums.length <= 2 * 10^5
nums.length is even
1 <= |nums[i]| <= 10^5
nums consists of equal number of positive and negative integers.

Solution

/**
 * @param {number[]} nums
 * @return {number[]}
 */
var rearrangeArray = function(nums) {
    const positiveNums = nums.filter(x => x > 0);
    const negativeNums = nums.filter(x => x < 0);
    const answer = [];
    
    for (let i = 0; i < nums.length / 2; i++) {
        answer.push(positiveNums[i], negativeNums[i]);
    }

    return answer;
};

LeetCode Problem 1833. Maximum Ice Cream Bars

It is a sweltering summer day, and a boy wants to buy some ice cream bars.
At the store, there are n ice cream bars. You are given an array costs of length n, where costs[i] is the price of the ith ice cream bar in coins. The boy initially has coins coins to spend, and he wants to buy as many ice cream bars as possible.
*Note: The boy can buy the ice cream bars in any order.
Return the maximum number of ice cream bars the boy can buy with coins coins.
You must solve the problem by counting sort.

Examples

Example 1:
Input: costs = [1,3,2,4,1], coins = 7
Output: 4
Explanation: The boy can buy ice cream bars at indices 0,1,2,4 for a total price of 1 + 3 + 2 + 1 = 7.
Example 2:
Input: costs = [10,6,8,7,7,8], coins = 5
Output: 0
Explanation: The boy cannot afford any of the ice cream bars.
Example 3:
Input: costs = [1,6,3,1,2,5], coins = 20
Output: 6
Explanation: The boy can buy all the ice cream bars for a total price of 1 + 6 + 3 + 1 + 2 + 5 = 18.

Constraints

costs.length == n
1 <= n <= 10^5
1 <= costs[i] <= 10^5
1 <= coins <= 10^8

Solution

/**
 * @param {number[]} costs
 * @param {number} coins
 * @return {number}
 */
var maxIceCream = function(costs, coins) {
    let iceCreamCount = 0;
    costs.sort((a, b) => a - b);

    for (const cost of costs) {
        if (cost > coins) {
            break;
        } else {
            coins -= cost;
            iceCreamCount++;
        }
    }

    return iceCreamCount;
};

Programmers Problem lev.2 숫자 변환하기

자연수 x를 y로 변환하려고 합니다. 사용할 수 있는 연산은 다음과 같습니다.
- x에 n을 더합니다
- x에 2를 곱합니다.
- x에 3을 곱합니다.
자연수 x, y, n이 매개변수로 주어질 때, x를 y로 변환하기 위해 필요한 최소 연산 횟수를 return하도록 solution 함수를 완성해주세요. 이때 x를 y로 만들 수 없다면 -1을 return 해주세요.

제한사항

1 ≤ x ≤ y ≤ 1,000,000
1 ≤ n < y

Solution

시간 초과된 풀이

function solution(x, y, n) {
    let answer = -1;
    const valueSet = new Set();
    const queue = [[x, 0]];
    
    while (queue.length) {
        const [value, count] = queue.shift();
        valueSet.add(value);
        
        if (value === y) {
            return count;
        }
        
        if (value > y) {
            continue;
        }
        
        if (!valueSet.has(value + n)) {
            queue.push([value + n, count + 1]);
        }
        
        if (!valueSet.has(value * 2)) {
            queue.push([value * 2, count + 1]);
        }
        
        if (!valueSet.has(value * 3)) {
            queue.push([value * 3, count + 1]);
        }
    }
    
    return answer;
}

다른 사람 풀이 참고 (DP)

function solution(x, y, n) {
    var answer = 0;
    const dp = new Array(y + 1).fill(Infinity);
    dp[x] = 0;
    for (let i = x; i <= y; i++) {
        dp[i + n] = Math.min(dp[i + n], dp[i] + 1);
        dp[i * 2] = Math.min(dp[i * 2], dp[i] + 1);
        dp[i * 3] = Math.min(dp[i * 3], dp[i] + 1);
    }
    return dp[y] === Infinity ? - 1 : dp[y];
}

LeetCode Problem 1325. Delete Leaves With a Given Value

Given a binary tree root and an integer target, delete all the leaf nodes with value target.
Note that once you delete a leaf node with value target, if its parent node becomes a leaf node and has the value target, it should also be deleted (you need to continue doing that until you cannot).

Examples

Example 1:
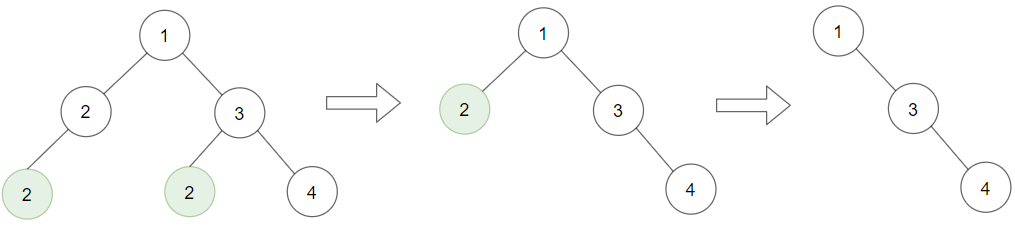
- Input: root = [1,2,3,2,null,2,4], target = 2
- Output: [1,null,3,null,4]
- Explanation:
  - Leaf nodes in green with value (target = 2) are removed (Picture in left).
  - After removing, new nodes become leaf nodes with value (target = 2) (Picture in center).

Example 2:
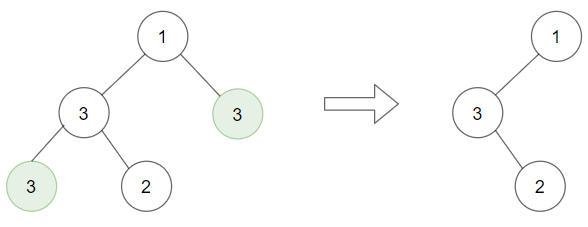
- Input: root = [1,3,3,3,2], target = 3
- Output: [1,3,null,null,2]

Example 3:
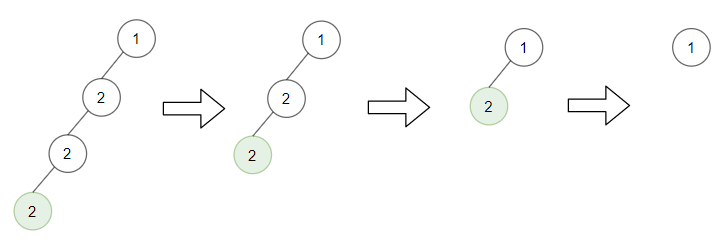
- Input: root = [1,2,null,2,null,2], target = 2
- Output: [1]
- Explanation:
  - Leaf nodes in green with value (target = 2) are removed at each step.

Constraints

The number of nodes in the tree is in the range [1, 3000].
1 <= Node.val, target <= 1000

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} target
 * @return {TreeNode}
 */
var removeLeafNodes = function(root, target) {
    const dfs = (node) => {
        if (!node) {
            return null;
        }

        const { val, left, right } = node;

        node.left = dfs(left);
        node.right = dfs(right);

        return val === target && !node.right && !node.left ? null : node;

    };

    return dfs(root);
};