Algorithm - Tree Problems

LeetCode Problem : Merge Two Binary Trees

• You are given two binary trees root1 and root2.

• Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.

• Return the merged tree.

  • Note:
    • The merging process must start from the root nodes of both trees.
  • *Constraints:
    • The number of nodes in both trees is in the range [0, 2000].
    • -10^4 <= Node.val <= 10^4

• Example1:

  • Input: root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
  • Output: [3,4,5,5,4,null,7]

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {TreeNode}
 */
var mergeTrees = function(root1, root2) {
    
    function dfs(node1, node2) {
        node1.val = node1.val + node2.val;
        if (node1.left && node2.left) {
            dfs(node1.left, node2.left)
        } else if (node2.left) {
            node1.left = node2.left;
        }

        if (node1.right && node2.right) {
            dfs(node1.right, node2.right)
        } else if (node2.right) {
            node1.right = node2.right;
        }
        
    }
    if (!root1) {
        return root2;
    }
    if (!root2) {
        return root1;
    }
    dfs(root1, root2);
    return root1;
};

LeetCode Problem : Increasing Order Search Tree

• Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

• Example 1:

  • input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
  • output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var increasingBST = function(root) {
    let data = [];
    dfs(root);
    
    function dfs(node) {
        if (node.left) dfs(node.left);
        if (node) data.push(node.val);
        if (node.right) dfs(node.right);
    }
    
    let rootNode = new TreeNode(data.splice(0,1));
    let currNode = rootNode;
    let nextNode;
    
    while(data.length) {
        nextValue = data.shift();
        nextNode = new TreeNode(nextValue);
        currNode.right = nextNode;
        currNode = nextNode;
    }
    
    return rootNode;
};

LeetCode Problem : Average of Levels in Binary Tree

• Given the root of a binary tree, return the average value of the nodes on each level in the form of an array. Answers within 10^-5 of the actual answer will be accepted.

• Example 1:

  • Input: root = [3,9,20,null,null,15,7]
  • Output: [3.00000,14.50000,11.00000]
  • Examplation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.
    Hence return [3, 14.5, 11].

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var averageOfLevels = function(root) {
    let result = [];
    let queue = [root];
    let level;
    let levelNodeCount;
    let node;
    let average;
    
    while (queue.length) {
        level = [];
        levelNodeCount = queue.length;
        
        for (let i = 0; i < levelNodeCount; i++) {
            node = queue.shift();
            level.push(node.val);
            
            if (node.left) queue.push(node.left);
            if (node.right) queue.push(node.right);
        }
        
        average = level.reduce((sum, value) => sum + value, 0) / levelNodeCount;
        result.push(average);
    }
    
    return result;
};

LeetCode : Converted Sorted Array to Binary Search Tree

• Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.
  • A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var sortedArrayToBST = function(nums) {
    if (!nums.length) return null;
    let midIndex = Math.floor(nums.length / 2);
    let root = new TreeNode(nums[midIndex]);
    root.left = sortedArrayToBST(nums.slice(0, midIndex));
    root.right = sortedArrayToBST(nums.slice(midIndex + 1));
    return root;
};

LeetCode : Sum of Root To Leaf Binary Numbers

• You are given the root of a binary tree where each node has a value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit.

  • For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.

• For all leaves in the tree, consider the numbers represented by the path from the root to that leaf. Return the sum of these numbers.

• The test cases are generated so that the answer fits in a 32-bits integer.

  • Constraints:
    • The number of nodes in the tree is in the range [1, 1000].
    • Node.val is 0 or 1.

• Example 1:

  • Input: root = [1,0,1,0,1,0,1]
  • Output: 22
  • Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

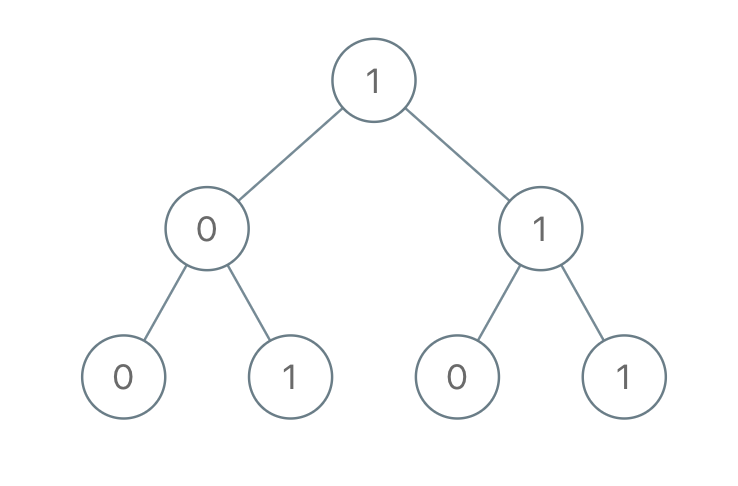
• Example 2:
  • Input: root = [0]
  • Output: 0

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var sumRootToLeaf = function(root) {
    
    function dfs(node, str) {
        if (!node) return 0;
        str += node.val;
        if (!node.left && !node.right) return parseInt(str, 2);
        return dfs(node.left, str) + dfs(node.right, str);
    }
    
    return dfs(root, '');
};

• 풀이
  • dfs(root, '')
    • str : '1'
    • return value : dfs(0, '1') + dfs(1, '1') = 9 + 13 = 22
  • dfs(0, '1')
    • str : '10'
    • return value : dfs(0, '10) + dfs(1, '10') = 4 + 5 = 9
  • dfs(0, '10)
    • str : '100'
    • return value : parseInt('100', 2) = 4
  • dfs(1, '10)
    • str : '101'
    • return value : parseInt('101', 2) = 5
  • dfs(1, '1')
    • str : '11'
    • return value : dfs(0, '11') + dfs(1, '11') = 6 + 7 = 13
  • dfs(0, '11')
    • str : '110'
    • return value : parseInt('110', 2) = 6
  • dfs(1, '11')
    • str: '111'
    • return value : parseInt('111', 2) = 7

LeetCode Problem : Binary Search Tree to Greater Sum Tree

• Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.

• As a reminder, a binary search tree is a tree that satisfies these constraints:

  • The left subtree of a node contains only nodes with keys less than the node's key.
  • The right subtree of a node contains only nodes with keys greater than the node's key.
  • Both the left and right subtrees must also be binary search trees.

• Example 1:

  • Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
  • Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var bstToGst = function(root) {
    const data = [];

    function dfs(node) {
        if (node.left) dfs(node.left);
        if (node !== null) data.push(node.val);
        if (node.right) dfs(node.right);
    }

    dfs(root);

    function makeGreaterTree(root) {
        const queue = [root];
        let node, sum;

        while (queue.length) {
            node = queue.shift();
            sum = data.reduce((accumulator, value) => {
                if (value > node.val) {
                    accumulator += value;
                }
                return accumulator;
            }, 0);
            node.val += sum;

            if (node.left) queue.push(node.left);
            if (node.right) queue.push(node.right);
        }
    }

    makeGreaterTree(root);

    return root;
};

LeetCode Problem : Maximum Binary Tree

• You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

Create a root node whose value is the maximum value in nums.
Recursively build the left subtree on the subarray prefix to the left of the maximum value.
Recursively build the right subtree on the subarray suffix to the right of the maximum value.
Return the maximum binary tree built from nums.

• Example 1:
  • Input: nums = [3,2,1,6,0,5]
  • Output: [6,3,5,null,2,0,null,null,1]
  • Explanation:
    • The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].
      • The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
        • Empty array, so no child.
      • The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
        • Empty array, so no child.
        • Only one element, so child is a node with value 1.
    • The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
      • Only one element, so child is a node with value 0.
      • Empty array, so no child.

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var constructMaximumBinaryTree = function(nums) {
    if (!nums.length) return null;
    let max = Math.max(...nums);
    let maxIndex = nums.indexOf(max);
    let root = new TreeNode(max);
    root.left = constructMaximumBinaryTree(nums.slice(0, maxIndex));
    root.right = constructMaximumBinaryTree(nums.slice(maxIndex + 1))
    return root;
};

LeetCode Problem : Find a Corresponding Node of a Binary Tree in a Clone of That Tree

• Given two binary trees original and cloned and given a reference to a node target in the original tree.

• The cloned tree is a copy of the original tree.

• Return a reference to the same node in the cloned tree.

• Note that you are not allowed to change any of the two trees or the target node and the answer must be a reference to a node in the cloned tree.

• Example 1:

  • Input: tree = [7,4,3,null,null,6,19], target = 3
  • Output: 3
  • Explanation:
    • In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.

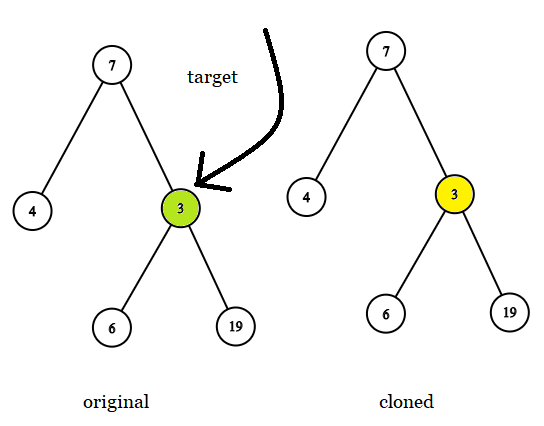
Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} original
 * @param {TreeNode} cloned
 * @param {TreeNode} target
 * @return {TreeNode}
 */

var getTargetCopy = function(original, cloned, target) {
    let queue = [[original, cloned]];
    
    while(queue.length) {
        
        for(let [oNode, cNode] of queue) {
            if(oNode === target) return cNode;
            if(oNode.left) queue.push([oNode.left, cNode.left]);
            if(oNode.right) queue.push([oNode.right, cNode.right]);
        }
    }
};

LeetCode Problem : Construct Binary Search Tree from Preorder Traversal

• Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.

• It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.

• A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.

• A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.

• Example 1:

  • Input: preorder = [8,5,1,7,10,12]
  • Output: [8,5,10,1,7,null,12]

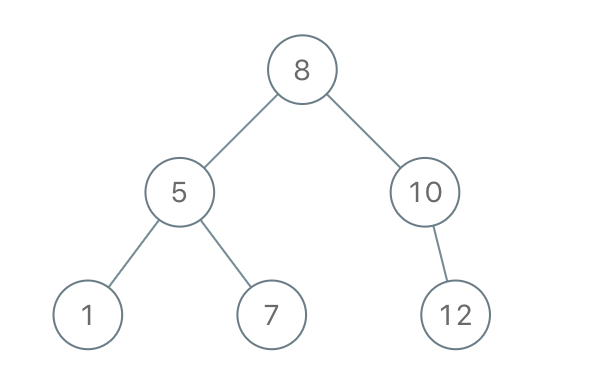
Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @return {TreeNode}
 */
var bstFromPreorder = function(preorder) {

    const insert = (node, value) => {
        if (node === null) {
            return new TreeNode(value);
        }

        if (value < node.val) {
            node.left = insert(node.left, value);
        } else {
            node.right = insert(node.right, value);
        }

        return node;
    }

    const root = new TreeNode(preorder[0]);

    for (let i = 1; i < preorder.length; i++) {
        insert(root, preorder[i]);
    }

    return root;
};

LeetCode Problem : Count Nodes Equal to Average of Subtree

• Given the root of a binary tree, return the number of nodes where the value of the node is equal to the average of the values in its subtree.

• Note :

  • The average of n elements is the sum of the n elements divided by n and rounded down to the nearest integer.
  • A subtree of root is a tree consisting of root and all of its descendants.

Examples

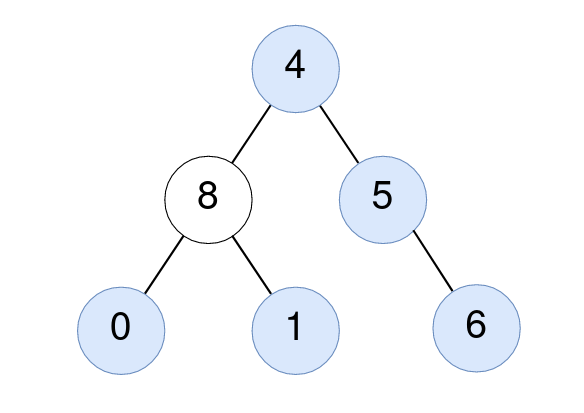
• Input: root = [4,8,5,0,1,null,6]
• Output: 5
• Explanation:
  • For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
  • For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
  • For the node with value 0: The average of its subtree is 0 / 1 = 0.
  • For the node with value 1: The average of its subtree is 1 / 1 = 1.
  • For the node with value 6: The average of its subtree is 6 / 1 = 6.

Constraints

• The number of nodes in the tree is in the range [1, 1000].
• 0 <= Node.val <= 1000

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var averageOfSubtree = function(root) {
    let averageEqualNodes = 0;

    const dfs = (node) => {
        if (!node) {
            return [0, 0];
        }
        const [leftSum, leftCount] = dfs(node.left);
        const [rightSum, rightCount] = dfs(node.right);

        const sum = leftSum + rightSum + node.val;
        const count = leftCount + rightCount + 1;
        if (Math.floor(sum/count) === node.val) {
            averageEqualNodes++;
        }
        return [sum, count];
    }

    dfs(root);

    return averageEqualNodes;
};