Homogeneous Coordinates

Homogeneous Coordinates

카메라로 영상을 촬영하였을 때 실제 3차원 공간의 좌표계, 카메라 좌표계, 영상 평면, 객체의 3차원 좌표계가 모두 다른데, 이 사이의 관계를 정의하기 위해서 기하학(Geometry)을 사용하게 된다.
이때 실제 3차원의 한 점$(x, y, z)$이 이미지 평면 상에 2차원 점$(x,y)$으로 투영 변환(projective transform) 되기 때문에 우리는 특히 사영 기하학(projective geometry)를 공부해야 한다.

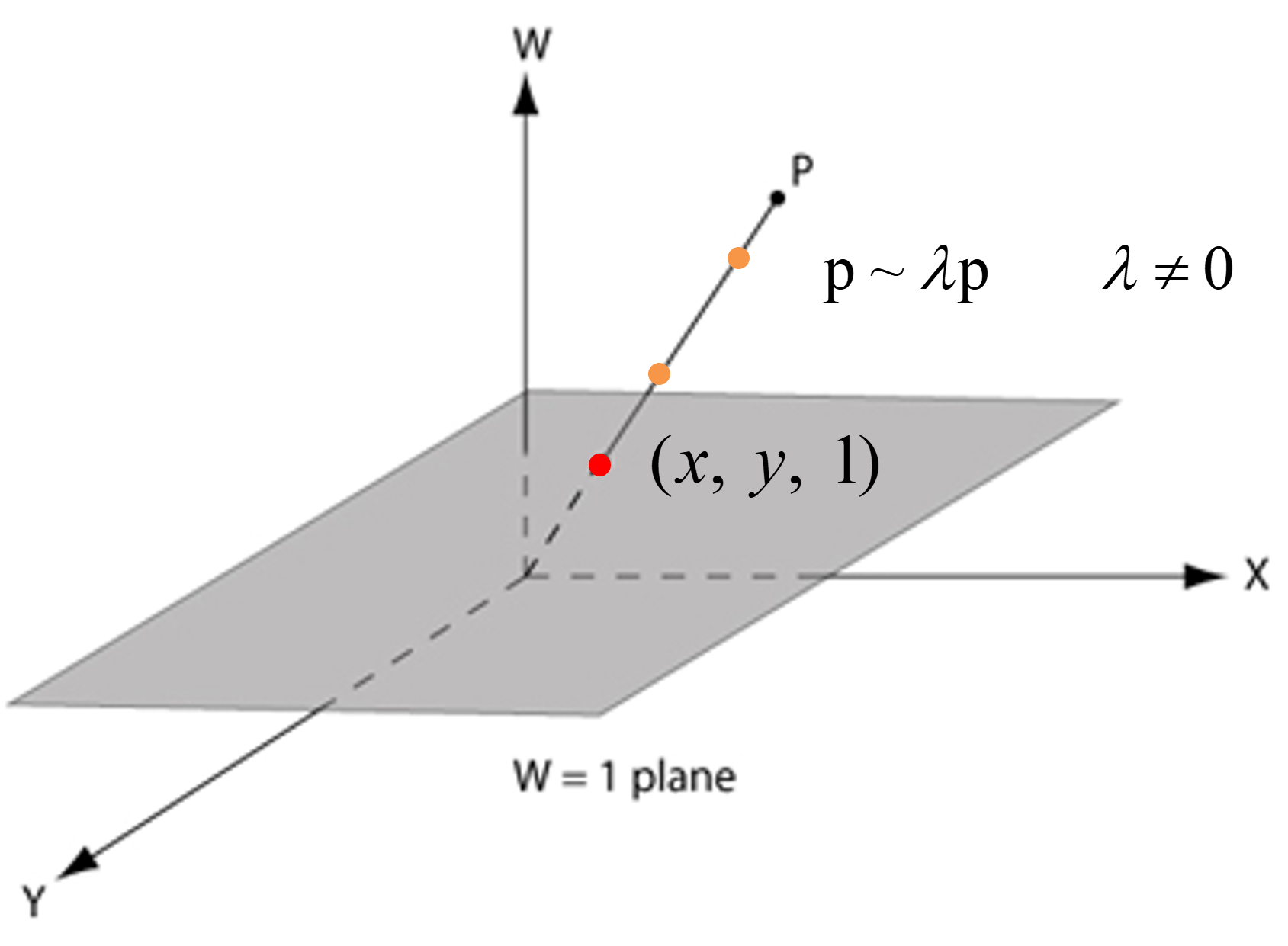
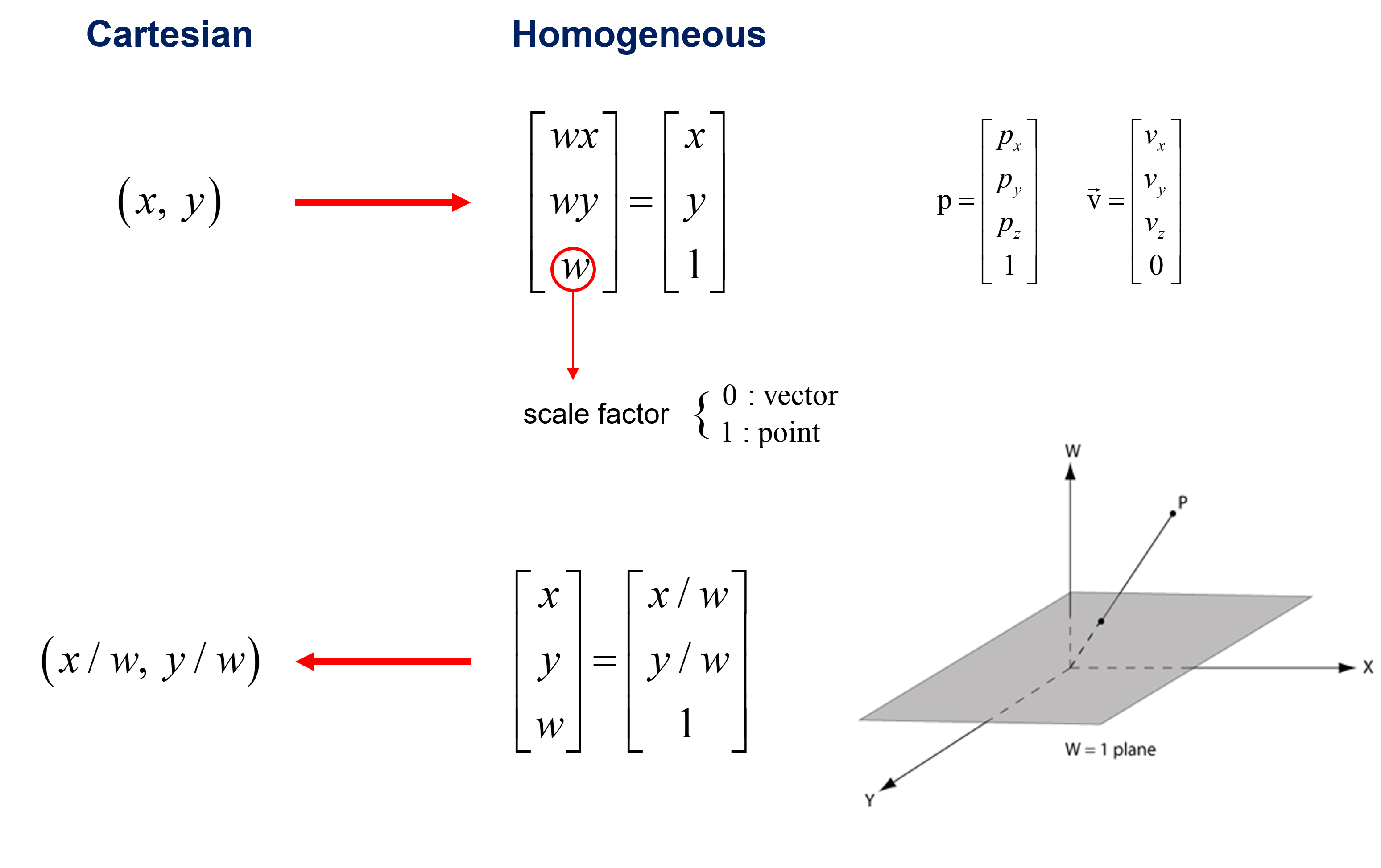
유클리드 공간(Euclidean space)에서 직교 좌표계(cartesian coordinate)를 사용하듯 projective geometry에서는 동차 좌표(homogeneous coordinate)를 사용하는 것이 편리하다. 동차 좌표는 2차원 평면 상의 점을 3차원 공간 상의 직선에 사상(mapping) 시킨 것으로 평면에서의 한 점을 2개의 좌표가 아닌 3개의 좌표를 사용하여 표현한다. 일반적으로 $n$차원의 사영 공간을 $n+1$개의 좌표로 나타낸다고 할 수 있다. 동차 좌표계는 직교 좌표계에서 0이 아닌 실수 $w$를 $x, y$에 곱한 후 마지막에 $w$로 요소를 하나 더 추가하는 것으로 표현한다. 점 $(x, y)$에 대한 동차 좌표 표현은 3차원의 한 직선 상에 무한히 존재한다. 즉, 한 점으로 변환되지 않는다. 또, 동차 좌표의 마지막 요소(argument) $w$를 scale factor로 사용하여 벡터와 점을 구별할 수 있다. 동차 좌표계에서 0이 아닌 $w$로 나누어주고 마지막 argument를 제거하면 직교 좌표계를 구할 수 있다. 다시 말해, 동차 좌표계를 직교 좌표계로 변환하는 것은 $w$의 scale과 상관없이 동차 좌표계 위의 한 직선에 있는 모든 점들을 $w=1$인 평면의 한 점으로 mapping 하는 것이다.

동차 좌표를 사용함으로써 다음과 같은 이점을 얻을 수 있다.
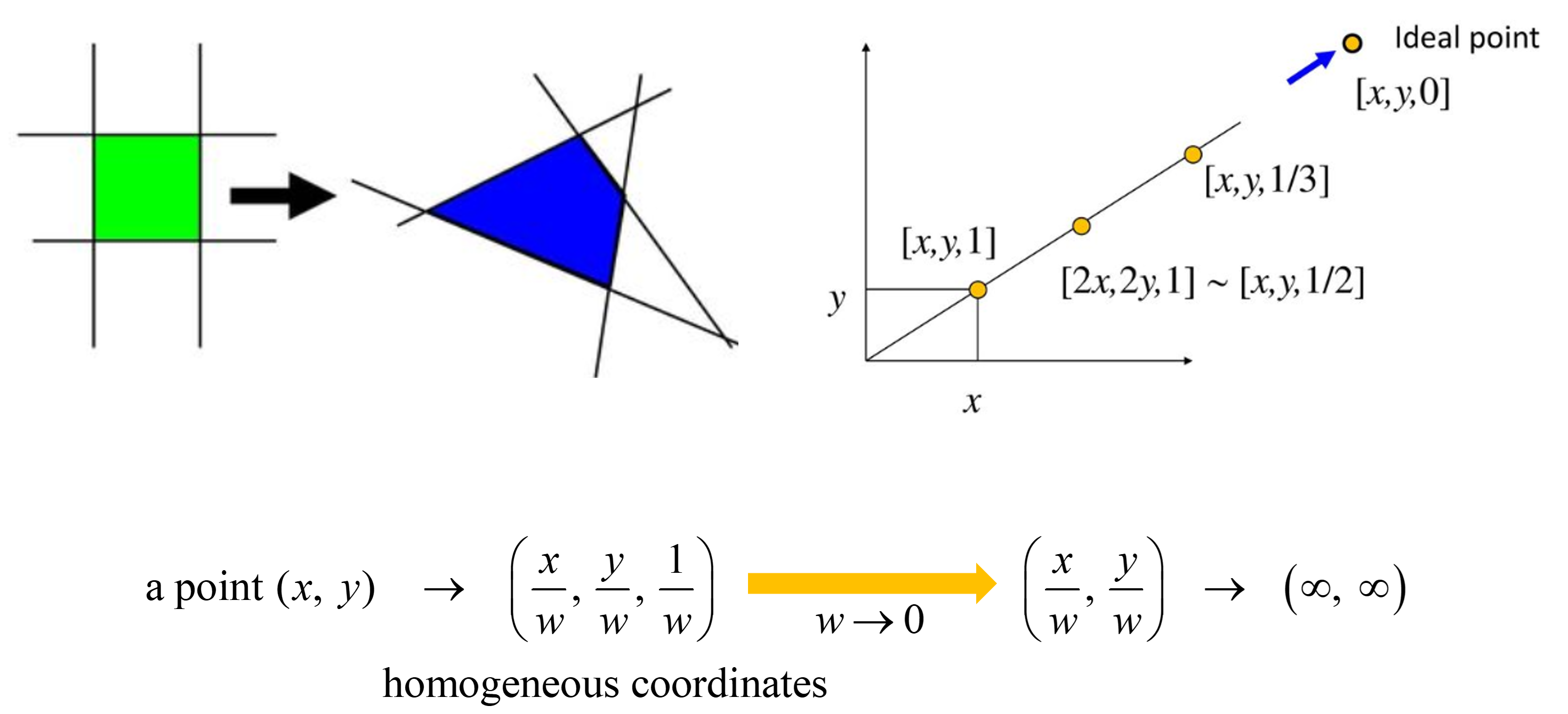
유클리드 공간에서 평행선은 절대 교차하지 않지만 원근감이 적용되는 사영 공간(각도, 길이, 평행성 보존 X)에서는 하나의 소실점에서 서로 만나게 된다. 이 소실점은 무한대 거리에 존재하는 무한 원점(point at infinity, ideal point)이기 때문에 유클리드 공간의 직교 좌표계에서 무한대를 표현할 수 없다. 따라서 무한대를 유한 좌표로 표현이 가능한 동차 좌표계를 사용하는 것이다. 점 $(x, y)$를 $\frac{1}{w}$를 곱한 동차 좌표로 변환하면 $(\frac{x}{w}, \frac{y}{w}, \frac{1}{w})$가 된다. $w$가 $0$이 되면 $(\frac{x}{w}, \frac{y}{w})$는 무한대로 이동하게 된다. 그러므로 동차 좌표 $(x, y, 0)$은 $(x, y)$ 방향으로의 무한대의 점이라고 할 수 있다.

또한 위치 변환(affine)이나 투영 변환(perspective/projective)은 단순한 선형 변환이 아니기 때문에 행렬 연산하기가 어렵지만 동차 좌표를 사용하게 되면 이를 결합한 변환까지 단일 행렬(single matrix)로 표현할 수 있다.

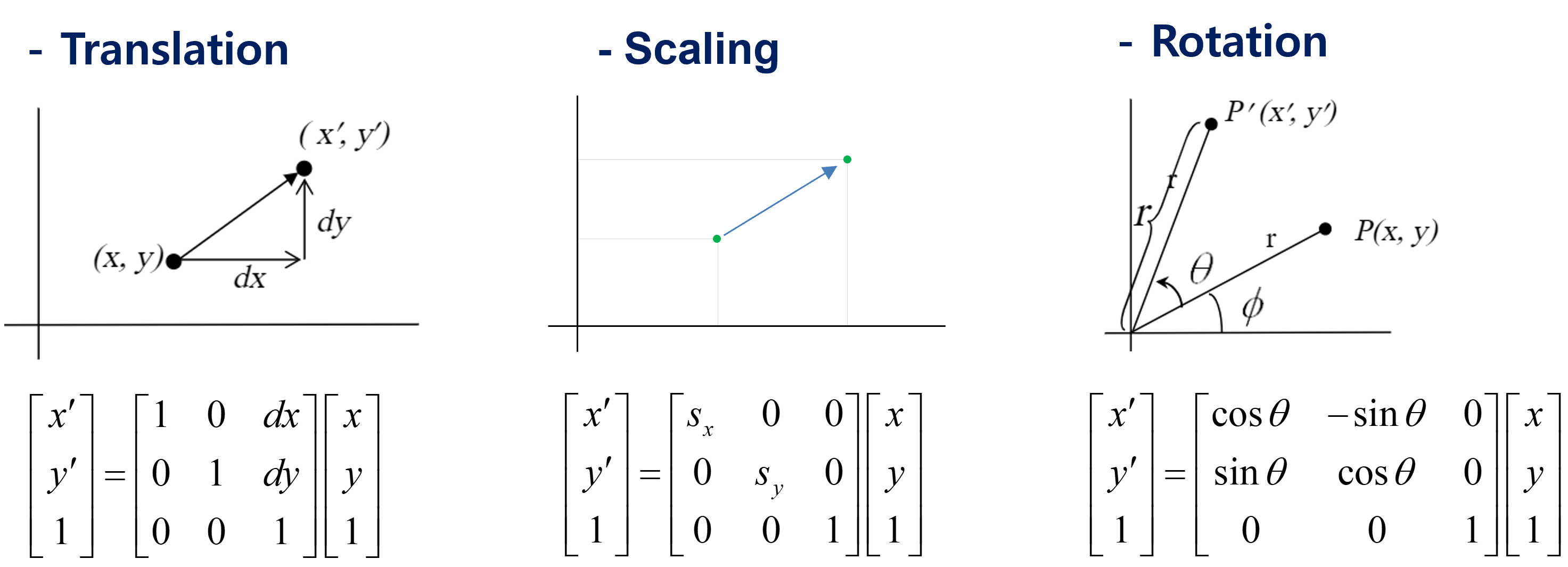
앞서, $w$의 크기와 상관없이 $(x, y)$에 대한 동차 좌표 표현은 3차원 공간 상의 한 직선 위에 존재하는 점들로 표현 가능하다고 했다. 이를 동치 관계(equivalence relation)라고 할 수 있다.