
선형 회귀 모델을 위한 데이터 변환 p347
- 특히 target은 정규 분포 형태가 아닌 특정값의 분포가 치우친 왜곡(Skew)된 형태의 분포도일 경우 예측 성능에 부정적인 영향을 미칠 가능성이 높다.
- 따라서 선형 회귀 모델을 적용하기 전에 먼저 데이터에 대한 스케일링/정규화 작업을 수행하는 것이 일반적이다.
- StandardScaler 클래스를 이용해 평균이 0, 분산이 1인 표준 정규 분포를 가진 dataset으로 변환하거나 MinMaxScaler 클래스를 이용해 최솟값이 0이고, 최대값이 1인 값으로 정규화를 수행한다.
- 스테일링/정규화를 수행한 dataset에 다시 다항 특성을 적용하여 변환하는 방법이다.
보통 1번 방법을 통해 예측 성능에 향상이 없을 경우 이와 같은 방법을 적용한다.- 원래 값에 log 함수를 적용하면 보다 정규 분포에 가까운 형태로 값이 분포하게 된다.
이러한 변환을 로그 변환(Log Transformation)이라고 부른다. 로그 변환은 매우 유용한 변환이며, 실제로 선형 회귀에서는 앞에서 소개한 1,2번 방법보다 로그 변환이 훨씬 많이 사용되는 변환 방법이다.
왜냐하면 1번 방법의 경우 예측 성능 향상을 크게 기대하기 어려운 경우가 많으며 2번 방법의 경우 feature의 개수가 매우 많을 경우에는 다향 변환으로 생성되는 feature의 개수가 기하급수로 늘어나서 과적합의 이슈가 발생할 수 있기 때문이다.
- target 값의 경우는 일반적으로 로그 변환을 사용한다.
- 정규 분포 변환, 최대/최소값 정규화, 로그 변환과, degree를 추가할 때, 추가하지 않을 때로 나누어서 RMSE 값을 살펴 보겠다.
- 그리고 Ridge 클래스를 사용하며 alpha 값에 따른 변화도 같이 보도록 하겠다.
from sklearn.preprocessing import StandardScaler, MinMaxScaler, PolynomialFeatures
# method는 표준 정규 분포 변환(Standard), 최대값/최소값 정규화(MinMax), 로그변환(Log) 결정
# p_degree는 다향식 특성을 추가할 때 적용. p_degree는 2이상 부여하지 않음.
def get_scaled_data(method='None', p_degree=None, input_data=None):
if method == 'Standard':
scaled_data = StandardScaler().fit_transform(input_data)
elif method == 'MinMax':
scaled_data = MinMaxScaler().fit_transform(input_data)
elif method == 'Log':
scaled_data = np.log1p(input_data)
else:
scaled_data = input_data
if p_degree != None:
scaled_data = PolynomialFeatures(degree=p_degree, include_bias=False).fit_transform(scaled_data)
return scaled_data
# Ridge의 alpha값을 다르게 적용하고 다양한 데이터 변환방법에 따른 RMSE 추출.
alphas = [0.1, 1, 10, 100]
#변환 방법은 모두 6개, 원본 그대로, 표준정규분포, 표준정규분포+다항식 특성
# 최대/최소 정규화, 최대/최소 정규화+다항식 특성, 로그변환
scale_methods=[(None, None), ('Standard', None), ('Standard', 2),
('MinMax', None), ('MinMax', 2), ('Log', None)]
for scale_method in scale_methods:
X_data_scaled = get_scaled_data(method=scale_method[0], p_degree=scale_method[1],
input_data=X_data)
print(X_data_scaled.shape, X_data.shape)
print('\n## 변환 유형:{0}, Polynomial Degree:{1}'.format(scale_method[0], scale_method[1]))
get_linear_reg_eval('Ridge', params=alphas, X_data_n=X_data_scaled,
y_target_n=y_target, verbose=False, return_coeff=False)
- 결과를 보면 표준 정규 분포와 최대/최소값 정규화로 feature dataset을 변경해도 성능의 개선이 없다.
- 2차 다항식으로 변환했을 경우 성능 개선이 있지만 다항식 변환은 feature의 개수가 많을 경우 적용하지 힘들고, 데이터가 많아지면 계산에 많은 시간이 소모된다.
- 반면에 로그 변환을 보면 모든 alpha 값에 대해 비교적 좋은 성능 향상이 있는 것을 알 수 있다.
로지스틱 회귀 p350
- 로지스틱 회귀는 선형 회귀 방식을
분류에 적용한 알고리즘이다. - 회귀가 선형인지 비선형인지는 독립 변수가 아닌
가중치(weight)가 선형인지 비선형인지를 따른다. - 로지스틱 회귀가 선형 회귀와 다른 점은 학습을 통해 선형 함수의 회귀 최적선을 찾는 것이 아니라
시그모이드(Sigmoid)함수 최적선을 찾고 이 시그모이드 함수의반환값을 확률로 간주해확률에 따라 분류를 결정한다는 것이다. - 많은 자연, 사회 현상에서 특정 변수의 확률 값은 선형이 아니라 시그모이드 함수와 같은
S자 커브 형태를 가진다. - 시그모이드 함수는
항상 0~1사이의 값을 가지며, x값이 커지면 1에 근사하고, x값이 작아지면 0에 근사한다. - 따라서 로지스틱 회귀는 회귀 문제를 분류 문제로 적용하기 위해 선형 회귀 방식과 시그모이드 함수를 이용하여 결과 값이 1과 0을 예측하도록 수행한다.
< Sigmoid Function>
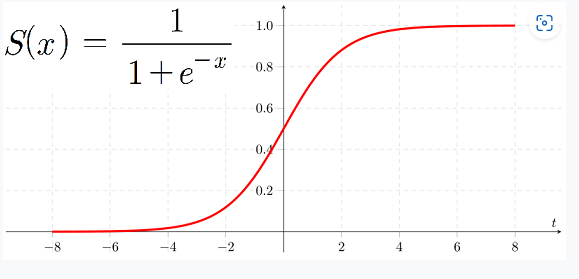
- 직선의 점의 y값을
확률로 생각하겠다.
cutoff 임계값, 분계점 (0.5보다 크면 다 1이라고 해!!!!)
음수는 확률이 없잖아!!! -> 문제점이 있다.
선형회귀는 이상치에 민감하다.
해결책은 로지스틱 곡선!!!
승산비!!!!!! odds ratio(p/1-p) 성공확률/실패확률
* 로릿함수 log(p / 1-p) x는(0-1) y축의( 무한 ) * <역함수관계> * 로지스틱함수 1/(1+e-x) x는 (무한) , y는 (0-1)
회귀 트리 p355
선형 회귀는 회귀 계수의 관계가 모두 선형이라고 가정하는 방식이며, 비선형 회귀 역시 회귀 계구의 관계가 비선형 회귀라고 가정하는 방식이다.
머신러닝 기반의 회귀는 회귀 계수를 기반으로 하는 최적 회귀 함수를 도출하는 것이 주요 목표이다.
하지만 회귀 함수를 기반으로 하지 않고 결정 트리와 같이 트리를 기반으로 하는 회귀 방식도 있다.
회귀를 위한 트리를 생성하고 이를 기반으로 회귀 예측을 하는 것이다.
4장의 분류 트리와 크게 다르지 않지만 리프 노드에서 예측 결정 값을 만드는 과정에 차이가 있는데, 분류 트리가 특정 클래스 label을 결정하는 것과 달리 회귀 트리는 리프 노드에 속한 데이터의 평균을 구해 회귀 예측값을 계산한다.
만약 feature가 하나만 있는 X feature dataset과 결정값 Y가 있다고 가정해보면, 결정 트리 기반으로 분할하면 X값의 균일도를 빈영한 지니 계수에 따라 규칙 노드들이 생기며 분할될 것이다.
리프 노드 생성 기분에 부합하는 트리 분할이 완료됬다면 리프 노드에 소속된 데이터 값의 평균값을 구해서 최종적으로 리프 노드에 결정 값으로 할당한다.
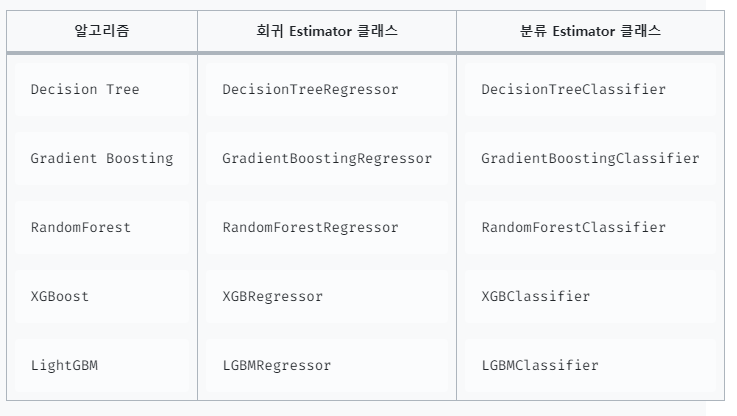
4장의 분류에서 소개한 모든 트리 기반의 알고리즘은 분류뿐만 아니라 회귀도 가능하다. 트리 생성이 CART(Classification And Regression Trees) 알고리즘에 기반하고 있기 때문이다.
자전거 대여 수요 예측 p362
자전거 대여 수요 예측 dataset에는 2011년 1월부터 2012년 12월까지 날짜/시간, 기온, 습도, 풍속 등의 정보를 기반으로 1시간 간격 동안의 자전거 대여 횟수가 기재되어 있다.
dataset의 주요 column은 다음과 같고, 결정값은 가장 마지막 column인 count로 '대여 횟수'를 의미한다.
datatime: hourly date + timestamp
season: 1=봄, 2=여름, 3=가을, 4=겨울
holiday: 1=토,일요일의 주말을 제외한 국경일 등의 휴일, 0=휴일이 아닌 날
workingday: 1=토,일요일의 주말 및 휴일이 아닌 주중, 0=주말 및 휴일
weather: 1=맑음, 약간 구름 낀 흐림, 2=안개, 안개+흐림, 3=가벼운 눈, 가벼운 비+천둥, 4=심한 눈/비, 천둥/번개
temp: 온도(섭씨)
atemp: 체감온도(섭씨)
humidity: 상대습도
windspeed: 풍속
casual: 사전에 등록되지 않는 사용자가 대여한 횟수
registered: 사전에 등록된 사용자가 대여한 횟수
count: 대여 횟수
#데이터 클렌징 가공 데이터 시각화 p363
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore", category=RuntimeWarning)
bike_df = pd.read_csv('/content/drive/MyDrive/book/bike_train.csv')
bike_df.info() # datetime column을 제외하면 전부 int 혹은 float 타입이다.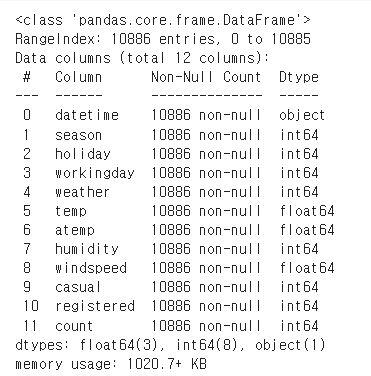
from datetime import datetime
# 문자열을 datetime으로 타입변경. p365
bike_df["datetime"] = bike_df["datetime"].astype("datetime64[ns]")# 년월일시간 추출하기 p365
#datetime column의 경우 년-월-일 시:분:초 문자 형식 , 처리가 필요하다.
#datetime을 년,월,일,시간의 4가지 속성으로 분리할텐데
# datetime 타입에서 년, 월, 일, 시간 추출
bike_df['year'] = bike_df.datetime.apply(lambda x : x.year)
bike_df['month'] = bike_df.datetime.apply(lambda x : x.month)
bike_df['day'] = bike_df.datetime.apply(lambda x : x.day)
bike_df['hour'] = bike_df.datetime.apply(lambda x: x.hour)
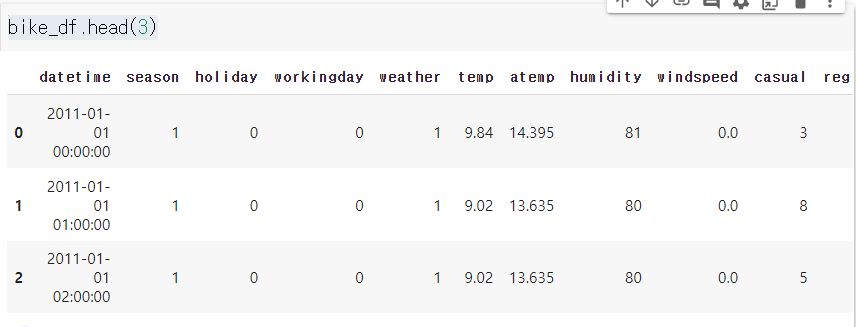
bike_df.head(3)# 필요없는 칼럼들 삭제한다.
drop_columns = ['datetime','casual','registered']
bike_df.drop(drop_columns, axis=1,inplace=True)- 캐글에서 요구한 성능 평가 방법은 RMSLE(Root Mean Square Log Error)로 오류 값의 로그에 대한 RMSE이다.
- 사이킷런은 RMSLE를 제공하지 않아 MSE와 RMSE, RMSLE를 모두 평가하는 함수를 만들어보겠다.
- 로그를 사용할 때 주의할 점은 numpy의 log()나 사이킷런의 mean_square_log_error()를 이용할 수도 있지만 데이터 값의 크기에 따라 overflow나 underflow가 발생하기 쉽다.
- 따라서 numpy의
log1p()를 이용하는데 이 함수는 1+log() 값으로overflow나 underflow문제를 해결해준다. - log1p()로 변환된 값은
exp1m() 함수로 복원할 수 있다.

로그 변환, feature 인코딩과 모델 학습/예측/평가 p368
- 회귀 모델을 이용하여 자전거 대여 횟수를 예측해보기 전에 결과값이 정규 분포인지 확인하는 것과 카테고리형 회귀 모델의 경우
ont-hot인코딩으로 feature를 인코딩해야한다. - 이유를 알아보기 위해 우선 LinearRegression 객체를 이용하여 회귀 예측을 해보겠다.

fig, axs = plt.subplots(figsize=(16, 8), ncols=4, nrows=2)
cat_features = ['year', 'month','season','weather','day', 'hour', 'holiday','workingday']
# cat_features에 있는 모든 칼럼별로 개별 칼럼값에 따른 count의 합을 barplot으로 시각화
for i, feature in enumerate(cat_features):
row = int(i/4)
col = i%4
# 시본의 barplot을 이용해 칼럼값에 따른 count의 평균값을 표현
sns.barplot(x=feature, y='count', data=bike_df, ax=axs[row][col]) 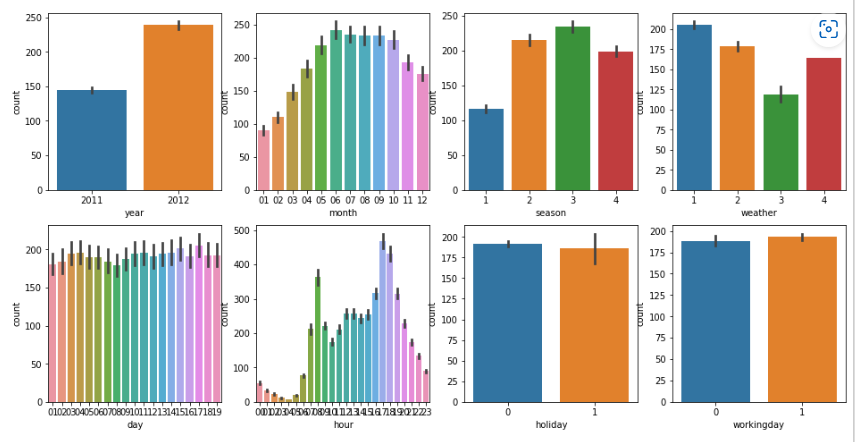
y_test.describe()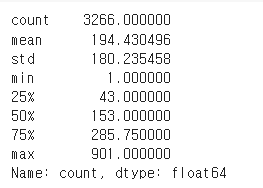
# y_tset와 preds 를 로그변환해서 mse() 구하면?
np.mean((np.log1p(y_test)- np.log1p(pred))**2)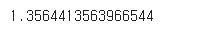
## p371
# 테스트 데이터 셋의 Target 값은 Log 변환되었으므로 다시 expm1를 이용하여 원래 scale로 변환
y_test_exp = np.expm1(y_test)
# 예측 값 역시 Log 변환된 타겟 기반으로 학습되어 예측되었으므로 다시 exmpl으로 scale변환
np.expm1(pred)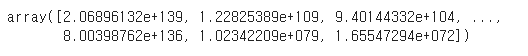
차원축소 Dimension Reduction p399
차원 축소는 매우 많은 feature로 구성된 다차원 dataset의 차원을 축소해 새로운 차원의 dataset을 생성하는 것이다.
일반적으로 차원이 증가할수록 데이터 포인트 간의 거리가 기하급수적으로 멀어지게 되고, 희소(sparse)한 구조를 가지게 된다. 즉, 데이터가 넓게 분포되어 있어 지역적으로 밀도가 적게 분포되어 있는 구조를 말한다. 수백 개 이상의 feature로 구성된 dataset의 경우 상대적으로 적은 차원에서 학습된 모델보다 예측 신뢰도가 떨어지며, 많은 feature를 가진 경우 개별 feature 간에 상관관계가 높을 가능성이 크다.
일반적으로 회귀 문제에서는 각각의 feature가 서로 독립이라고 가정한다.
하지만 실제 데이터에선 어떤 두 feature가 같이 증가하거나 감소하는 것과 같이 높은 상관관계를 가지게 되면 가정에 위배되어 모델의 예측 성능에 부정적인 영향을 미치게 된다.
이렇게 입력 변수 간의 상관관계가 높을 경우 이로 인해 모델의 예측 성능이 떨어지는 현상을 다중 공선성(Multicollinearity) 문제라고 부르고, 다차원의 dataset에선 다중 공선성 문제가 발생할 가능성이 크다.
그리고 매우 많은 다차원의 feature를 차원 축소해 feature 수를 줄이면 더 직관적으로 데이터를 해석할 수 있다. 또한 차원 축소를 할 경우 학습 데이터의 크기가 줄어들어서 학습에 필요한 처리 능력도 줄일 수 있다.
차원 축소는 피처 선택(feature selection)과 피처 추출(feature extraction)으로 나눌 수 있다. 피처 선택이란 특정 feature에 종속성이 강한 불필요한 feature는 아예 제거하고, 데이터의 특성을 잘 나타내는 주요 feature만 선택하는 것이다. 피처 추출은 기존 feature를 저차원의 중요 feature로 압축해서 추출하는 것이다. 이렇게 새로 추출된 중요 특성은 기존 feature와는 완전히 다른 값이 된다.
피처 추출은 기존 feature를 단순 압축이 아닌, feature를 함축적으로 더 잘 설명할 수 있는 또 다른 공간으로 매핑해 추출하는 것이다. 여러 가지 feature로 되어 있는 dataset이라면 이를 더 함축적인 요약 특성으로 추출할 수 있다. 이러한 함축적인 특성 추출은 기존 feature가 전혀 인지하지 어려웠던 잠재적인 요소(Latent Factor)를 추출하는 것을 의미한다. PCA, SVD, NMF는 잠재적인 요소를 찾는 대표적인 차원 축소 알고리즘이다. 매우 많은 의미를 가지는 이미지나 텍스트에서 차원 축소를 통해 잠재적인 의미를 찾아 주는 데 이러한 알고리즘들이 잘 활용되고 있다.
# iris 데이터 불러오기
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
iris = load_iris()
X = iris.data
y = iris.target
# (1) StandardScaler
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
#X_scaled
# (2) PCA차원 변환
from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
X_pca = pca.fit_transform(X_scaled)
#X_pca
# (3) 변동성 비율
print(" 3번: ",pca.explained_variance_ratio_)
# (4) 스케일링만 할때, RandomForestClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
rf_clf = RandomForestClassifier(random_state= 156)
print(" 4번 : ",cross_val_score(rf_clf, X_scaled, y,scoring ="accuracy",cv=3 ) )
# (5 ) 차원 변환 후, RandomForestClassifier
rf_clf = RandomForestClassifier (random_state= 156)
print( " 5번 : ",cross_val_score(rf_clf, X_pca, y,scoring ="accuracy",cv=3 ) )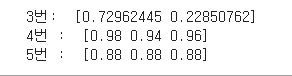
이미지 데이터의 Dimension Reduction
매우 많은 픽셀로 이루어진 이미지 데이터에서 잠재된 특성을 feature로 도출해 함축적 형태의 이미지 변환과 압축을 수행할 수 있다.
이렇게 변환된 이미지는 원본 이미지보다 훨씬 적은 차원이기 때문에 과적합 영향력이 작아져서 오히려 원본 데이터로 예측하는 것보다 예측 성능을 더 끌어 올릴 수 있다.
이미지 자체에 가지고 있는 차원의 수가 너무 크기 때문에 비슷한 이미지라도 약간의 픽셀 수 차이 땜문에 잘못된 예측으로 이어질 수 있다.
텍스트 데이터의 Dimension Reduction
텍스트 데이터에선 텍스트 문서의 숨겨진 의미를 추출하는 것으로 사용된다.
문서는 많은 단어로 구성되어 있고, 문서를 만드는 사람은 어떤 의미나 의도를 가지고 문서를 작성하면서 단어를 사용하게 된다.
일반적으로 사람들은 문서를 읽으면서 이 문서가 어떤 의미나 의도를 가지고 작성되었는지 쉽게 인지할 수 있다.
차원 축소 알고리즘은 문서 내 단어들의 구성에서 숨겨져 있는 시맨틱(Semantic) 의미나 토픽(Topic)을 잠재 요소로 간주하고 이를 찾아낼 수 있다.
SVD나 NMF는 이러한 시맨틱 토픽 모델링을 위한 기반 알고리즘으로 사용된다.
PCA(Principal Component Analysis)
PCA(Principal Component Analysis)는 가장 대표적인 차원 축소 방법이다.
PCA는 여러 변수 간에 존재하는 상관관계를 이용하여 이 변수들의 상관관계를 대표하는 주성분(Principal Component)을 추출해 차원을 축소하는 방법이다.
차원이 축소할 때 기존의 정보가 유실되지만 PCA를 이용할 때 유실되는 정보가 최소화된다.
PCA는 데이터가 주어져 있을 경우 그 데이터 각각의 값들에 대한 정보를 파악하는 것이 아니라 데이터의 분포에 대한 정보를 파악하는 것으로 가장 높은 분산을 가지는 데이터의 축을 찾아 이 축이 차원을 축소하게 되는 PCA의 주성분이 된다.
즉, 분산이 데이터의 특성을 가장 잘 나타내는 것으로 간주하고 있다.
PCA는 먼저 가장 큰 데이터 변동성(Variance)을 기반으로 첫번째 벡터 축을 생성하고, 두 번째 축은 이 벡터 축에 직각이 되는 벡터(직교 벡터)를 축으로 한다.
세번째 축은 다시 첫번째와 두번째 축에 직각이 되는 벡터를 축으로 설정하며 이러한 방식으로 축을 생성한다.
이렇게 생성된 벡터 축에 원본 데이터를 투영하면 벡터 축 개수만큼의 차원으로 차원 축소가 이루어진다.
즉, PCA는 이처럼 원본 데이터의 feature 개수에 비해 작은 주성분으로 원본 데이터의 총 변동성을 대부분 설명할 수 있는 분석법이다.
이론상으로 주성분은 최대 feature 개수만큼의 차원을 가질 수 있지만 차원 축소를 목적으로 실행하며 벡터 축이 점점 생성될수록 의미가 크지 않기 때문에 사용자가 적당히 축소할 차원 수를 설정한다.
PCA를 선형대수 관점에서 해석해보면, 입력 데이터의 공분산 행렬(Covariance Matrix)을 고유값 분해하고, 이렇게 구한 고유벡터에 입력 데이터를 선형 변환하는 것이다.
이 고유벡터가 PCA의 주성분 벡터로서 입력 데이터의 분산이 큰 방향을 나타낸다.
고유값(eigenvalue)은 이 고유벡터(eigenvector)의 크기를 나타내며, 동시에 입력 데이터의 분산을 나타낸다.
일반적으로 선형 변환은 특정 벡터에 션형 변환 행렬 A를 곱해 새로운 벡터로 변환하는 것을 의미하며, 특정 벡터를 한 공간에서 다른 공간으로 투영하는 개념으로도 볼 수 있다.
보통 분산은 한 개의 특정 변수에 대해 데이터의 변동을 의미하지만, 공분산은 두 변수 간의 변동을 의미한다.
공분산 행렬은 위 이미지와 같이 구할 수 있으며, 정방 행렬(Diagonal Matrix)이면서 대칭 행렬(Symmetric Matrix)이다.
이렇게 정방 행렬이면서 대칭 행렬이면 고유값 분해를 통해 교유 벡터를 직교 행렬(othogonal metrix)로, 고유값을 정방 행렬로 대각화할 수 있다.
따라서 공분산 행렬도 고유값 분해를 통해 C=P∑P T 나타낼 수 있다. 여기서 고유 벡터이 가장 큰 분산의 방향을 가진 고유 벡터이다.
credit card 데이터 세트 PCA 변환 p410
# header로 의미없는 첫행 제거, iloc로 기존 id 제거
df = pd.read_excel("/content/drive/MyDrive/book/default of credit card clients.xlsx", header=1, sheet_name='Data').iloc[0:,1:]
# 칼럼명 변경, y_target 특정하기
df.rename(columns={'PAY_0':'PAY_1','default payment next month':'default'}, inplace=True)
y_target = df['default']
X_features = df.drop('default', axis=1)
print(df)
# 시각화 하기
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
corr = X_features.corr()
plt.figure(figsize=(14,14))
print( sns.heatmap(corr, annot=True, fmt='.1g'))
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
#BILL_AMT1 ~ BILL_AMT6 까지 6개의 속성명 생성
cols_bill = ['BILL_AMT'+str(i) for i in range(1,7)]
print('대상 속성명:',cols_bill)
# 2개의 PCA 속성을 가진 PCA 객체 생성하고, explained_variance_ratio_ 계산 위해 fit( ) 호출
scaler = StandardScaler()
df_cols_scaled = scaler.fit_transform(X_features[cols_bill])
X_features.loc[:, cols_bill] = df_cols_scaled
pca = PCA(n_components=2)
pca.fit(df_cols_scaled)
print('PCA Component별 변동성:', pca.explained_variance_ratio_)(1) 데이터
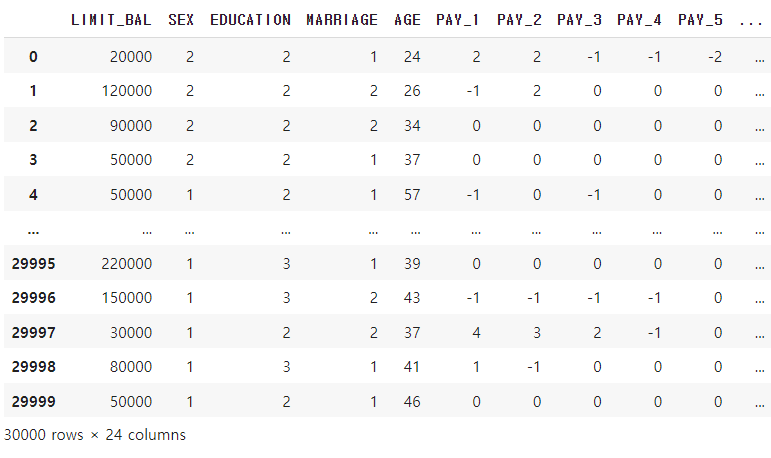
(2) 시각화
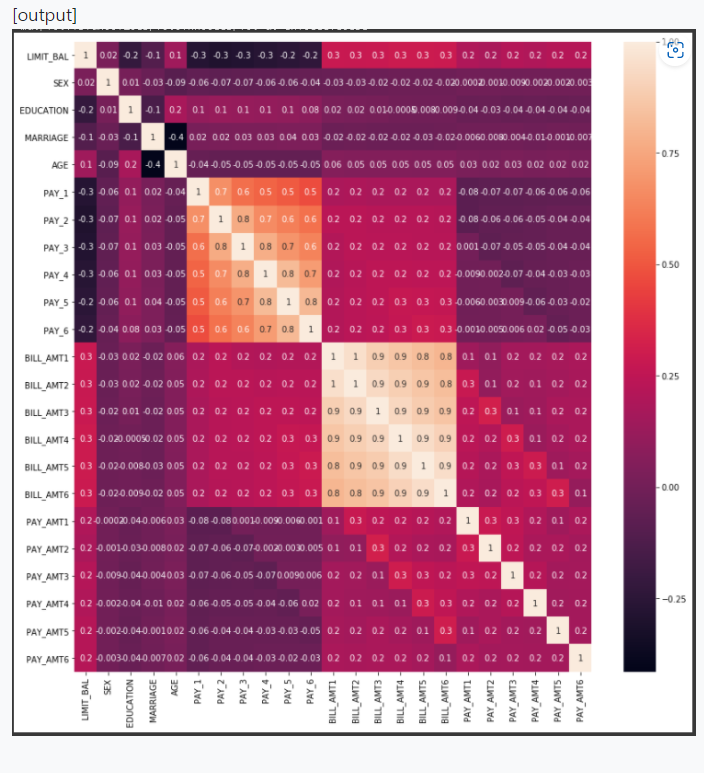
(3)

credit card 문제
import pandas as pd
# header로 의미없는 첫행 제거, iloc로 기존 id 제거, (책 p410)
df = pd.read_excel("/content/drive/MyDrive/book/default of credit card clients.xlsx", header=1, sheet_name='Data').iloc[0:,1:]
# 칼럼명 변경, y_target 별도 지정 (책 p411)
df.rename(columns={'PAY_0':'PAY_1','default payment next month':'default'}, inplace=True)
y_target = df['default']
X_features = df.drop('default', axis=1)
# 선생님이 칼럼이 많아서 잘랐다.
df =df.iloc[:,11:17]
print(" 0번 : ",df)
'''
~~ 여기서 부터 문제 ~~
1. scaling
2. PCA변환
3. PCA 변환 전 LogisticRegression으로 분류 ,cv= 5
4. PCA 변환 후 LogisticRegression으로 분류 , cv=5
'''
## 1. scaling
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_features)
print(" 1번 : ",X_scaled)
## 2. PCA변환하기
from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
X_pca = pca.fit_transform(X_scaled)
print(" 2번 : ",X_pca)
## 3. PCA 변환 이전에 대하여 LogisticRegression으로 분류 , cv=5
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
rf_clf = LogisticRegression(random_state= 156)
print(" 3번 : ",cross_val_score(rf_clf, X_scaled,y_target,scoring ="accuracy",cv=5 ) )
## 4. PCA 변환한 데이터프레임 대하여 LogisticRegression으로 분류 ,cv= 5
rf_clf = LogisticRegression(random_state= 156)
print( " 4번 : ",cross_val_score(rf_clf, X_pca, y_target,scoring ="accuracy",cv=5 ))(0) 데이터
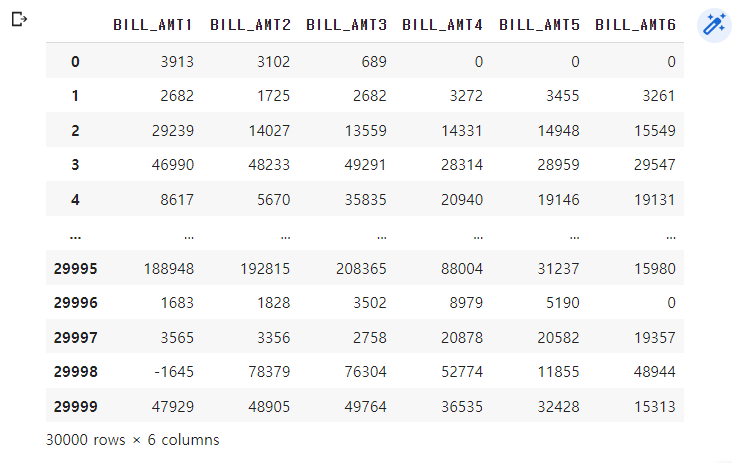
(1) 스케일링
(2) PCA 변환

(3, 4) 결과값 비교

출처:
https://velog.io/@sset2323/05-08.-%ED%9A%8C%EA%B7%80-%ED%8A%B8%EB%A6%AC