https://colab.research.google.com/drive/1C0wiUh8O17FxTDiDHxxmg_dmsEmk2rvb#scrollTo=Js2tpji8QPkV
t분포
t 분포란?
t 분포는 모집단 표준편차를 알 수 없을 때 표본 평균과 모집단 평균 사이 표준화된 거리를 설명하며, 관측값은 정규 분포를 따르는 모집단에서 추출됩니다.
t 분포가 스튜던트 t 분포와 동일한가?
예.
t 분포와 z 분포 간 주요 차이점은 무엇인가?
표준 정규 분포 또는 z 분포에서는 모집단 표준편차를 알고 있다고 가정합니다. t 분포는 표본 표준편차를 근거로 합니다.
t 분포와 정규 분포 비교
t 분포는 정규 분포와 비슷합니다. 분포에 대한 정확한 수학적 정의가 내려져 있습니다. 복잡한 수학을 다루는 대신 t 분포의 유용한 특성과 분석에서 중요한 이유에 대해 알아보겠습니다.
정규 분포와 마찬가지로 t 분포의 모양도 매끄럽습니다.
정규 분포와 마찬가지로 t 분포도 대칭형입니다. 평균에서 반으로 접는다고 생각해보면 양쪽이 서로 동일할 것입니다.
표준 정규 분포(또는 z 분포)와 마찬가지로 t 분포의 평균도 0입니다.
정규 분포에서는 모집단 표준편차를 알고 있다고 가정합니다. t 분포에서는 이러한 가정을 내리지 않습니다.
t 분포는 자유도에 의해 정의됩니다. 자유도는 표본 크기와 관련이 있습니다.
t 분포는 모집단 표준편차를 알 수 없거나 두 가지 모두 적용될 때 작은 표본 크기에 가장 유용합니다.
표본 크기가 커질수록 t 분포가 정규 분포와 비슷해집니다.
다음 그래프에서 세 개의 t 분포와 하나의 표준 정규분포를 비교해 보여줍니다.
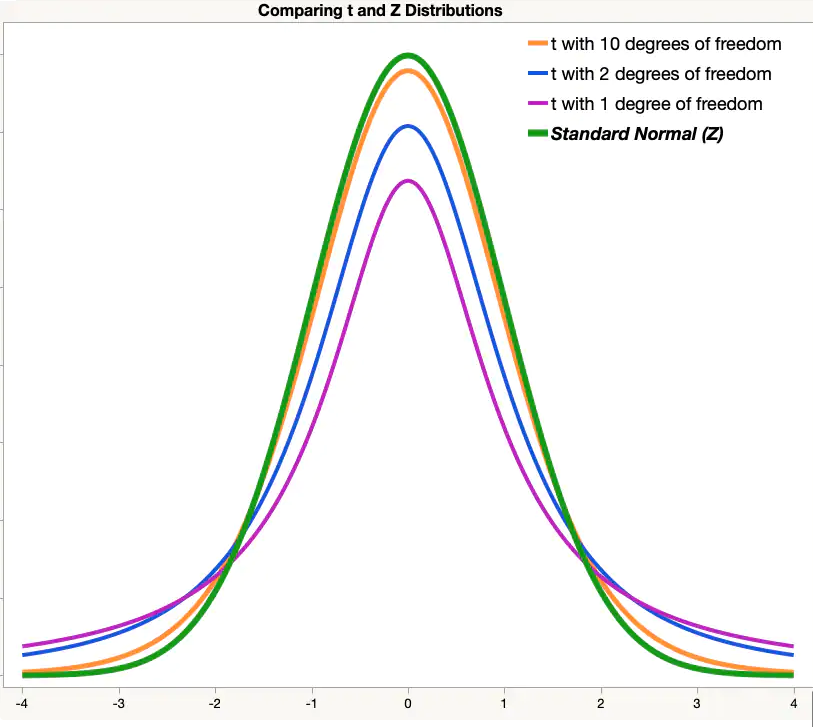
출처 : https://www.jmp.com/ko_kr/statistics-knowledge-portal/t-test/t-distribution.html