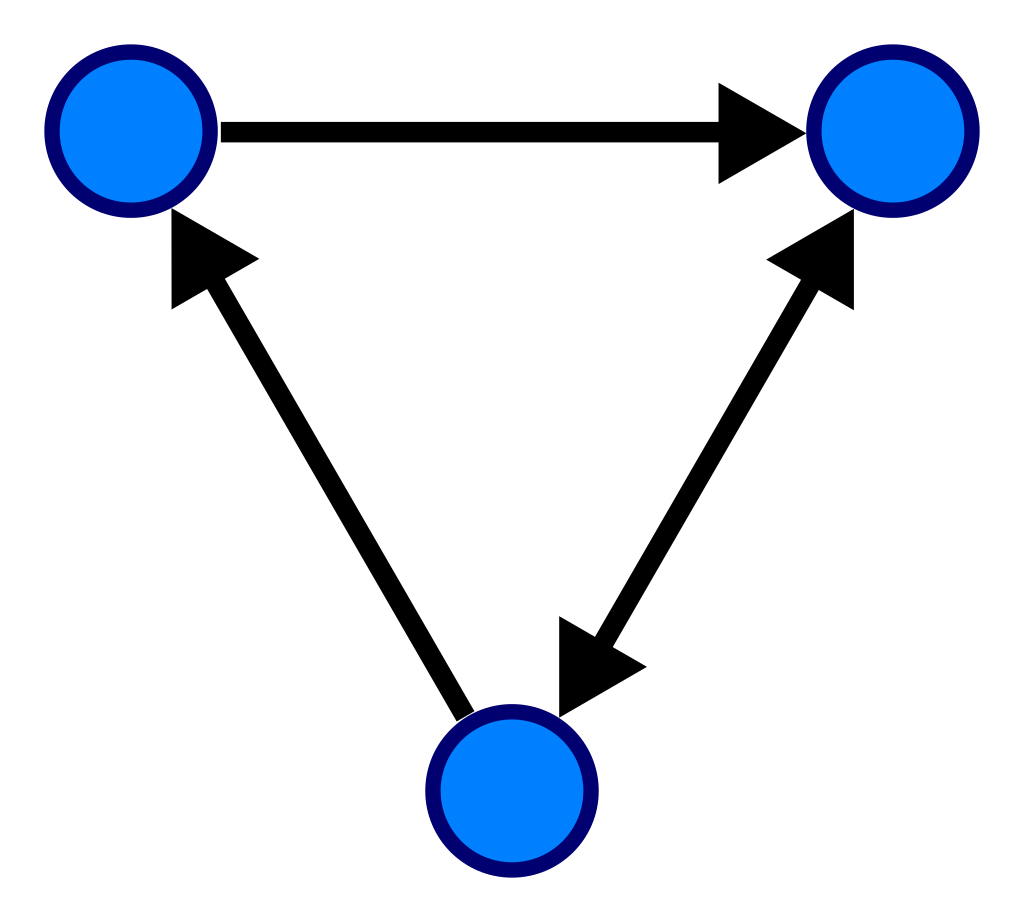
📍그래프 (Graph)란?

그래프(Graph)는 여러 개의 노드(node)와 이를 연결하는 간선(edge)들의 집합으로 구성된 자료구조입니다

그래프의 주요 특징

노드(Node 또는 Vertex)

그래프의 기본 단위로, 정보의 단위를 나타냅니다.

간선(Edge)

노드들을 연결하는 선으로, 노드 간의 관계를 표현합니다.
간선은 방향성이 있는 경우와 없는 경우로 나눌 수 있습니다.

• 방향성이 있는 간선 화살표로 표현됩니다.
• 무방향성은 단순한 선으로 표현됩니다.

방향성(Directionality)

그래프는 방향 그래프와 무방향 그래프로 나눌 수 있습니다.
간선에 방향이 있는 경우 방향 그래프, 없는 경우 무방향 그래프입니다.

가중치(Weight)

간선에 가중치가 할당될 수 있습니다.
이는 간선이 나타내는 관계의 강도나 비용을 나타냅니다.

차수(Degree)

무방향 그래프에서는 노드에 연결된 간선의 수를 차수라고 합니다.

진입 차수(In-Degree)

• 진입 차수는 방향 그래프에서 특정 노드로 들어오는 간선의 수를 나타냅니다.
• 특정 노드로 향하는 모든 간선들의 수를 세어서 해당 노드의 진입 차수를 계산합니다.
• 노드의 진입 차수는 해당 노드로 들어오는 연결의 총 수를 나타냅니다.

발신 차수(Out-Degree)

• 발신 차수는 방향 그래프에서 특정 노드에서 나가는 간선의 수를 나타냅니다.
• 특정 노드에서 향하는 모든 간선들의 수를 세어서 해당 노드의 발신 차수를 계산합니다.
• 노드의 발신 차수는 해당 노드에서 나가는 연결의 총 수를 나타냅니다.

경로(Path)

그래프에서 노드를 연결하는 간선들의 순서 있는 나열로, 노드 A에서 B로 가는 경로는 A, C, D, B와 같이 나타낼 수 있습니다.

연결성(Connectivity)

노드 간의 경로가 존재하면 해당 그래프는 연결 그래프입니다. 그렇지 않으면 비연결 그래프입니다.

사이클(Cycle)

한 노드에서 시작해서 다시 같은 노드로 돌아가는 경로를 의미합니다
즉, 단순 경로(모든 노드가 중복 없이 한 번씩만 방문되는 경로)의 시작 노드와 종료 노드가 동일한 경우를 나타냅니다.

그래프(Graph)의 종류

무방향 그래프(Undirected Graph) vs 방향 그래프(Directed Graph)

• 무방향 그래프(Undirected Graph)
  • 간선에 방향이 없는 그래프로, 노드 A에서 B로 가는 간선은 동시에 B에서 A로 가는 간선도 존재합니다.
• 방향 그래프(Directed Graph)
  • 간선에 방향이 있는 그래프로, 노드 A에서 B로 가는 간선이 있을 때, B에서 A로 가는 간선이 없습니다.

가중치 그래프(Weighted Graph)

• 간선에 가중치(Weight)가 할당된 그래프로, 간선이 나타내는 관계에 가중치가 추가됩니다.

연결 그래프(Connected Graph) vs 비연결 그래프(Disconnected Graph)

• 연결 그래프(Connected Graph)
  • 연결 그래프는 그래프 내의 임의의 두 노드에 대해 경로가 존재하는 그래프입니다.
  • 어떤 노드에서 출발해서 다른 모든 노드에 도달할 수 있는 그래프를 말합니다.
• 비연결 그래프(Disconnected Graph)
  • 비연결 그래프는 그래프 내에서 최소한 하나 이상의 노드 그룹이 서로 격리되어 있어, 이 그룹 간에는 경로가 존재하지 않는 그래프입니다.
  • 최소 하나의 노드 그룹이 다른 그룹과 연결되어 있지 않은 상태를 말합니다.

순환 그래프(Cyclic Graph) vs 비순환 그래프(Acyclic Graph)

• 순환 그래프(Cyclic Graph)
  • 순환 그래프는 한 노드에서 시작하여 돌아와서 다시 자기 자신으로 연결되는 경로가 있는 그래프입니다.
• 비순환 그래프(Acyclic Graph)
  • 순환을 포함하지 않는 그래프입니다.