분할정복이란?
분할 정복(Divide & Conquer)은 주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 부분 문제에 대한 답을 재귀 호출을 이용해 계산하고, 그 답으로부터 전체 문제의 답을 계산해 내는 알고리즘이다.
언뜻보면 일반적인 재귀 호출과 같아 보일 수 있는데, 재귀 호출과 다른 점은 문제를 거의 같은 크기의 문제로 나눈 다는 것.
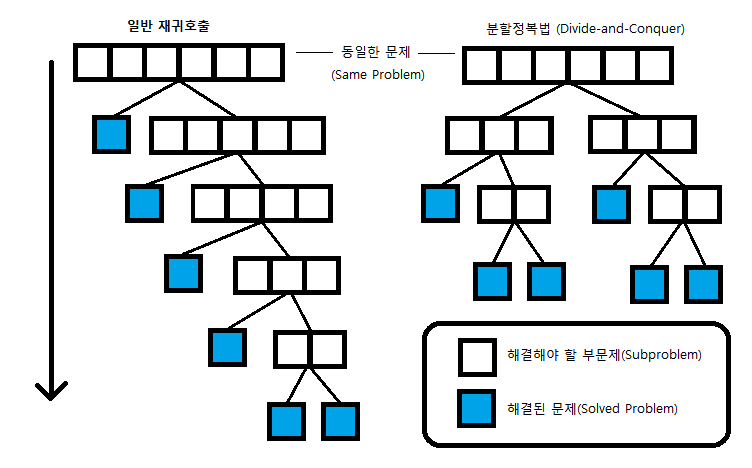
재귀는 한 문제만 똑 떼서 푸는 식으로 한다면, 분할 정복은 문제를 거의 같은 크기의 두 문제로 나누어서 해결한다.
수열의 합을 구하는 코드 두 개로 직접 비교해보자.
재귀를 이용한 수열의 합
int sum(int n){
if(n==1) return 1;
return sum(n-1) + n;
}분할 정복을 이용한 수열의 합
int fastsum(int n){
if(n==1) return 1;
if(n%2==1) return fastsum(n-1) + n;
return 2*fastsum(n/2) + (n/2) * (n/2);
}
// 왜 이 식이 나오는 지는 sum(n)을 수학적으로 써보면 바로 알 수 있다.이렇게 분할 정복을 이용하면 함수를 호출하는 횟수가 훨씬 적어진다.
분할 정복 구성요소
-
문제를 더 작은 문제로 분할하는 과정(Divide)
-
각 문제에 대한 답을 원래 문제에 대한 답으로 병합하는 과정(Merge)
-
답을 더이상 분할하지 않고 풀 수 있는 매우 작은 문제(base case)
분할 정복은 재귀 함수와 최악의 경우 시간 복잡도는 비슷하나, 보통의 경우에는 더 빠르게 처리해 준다.
병합 정렬(Merge Sort)
퀵 정렬은 동빈북에서 다루었으므로, 여기서는 병합 정렬에 대해서만 다루려고 한다.
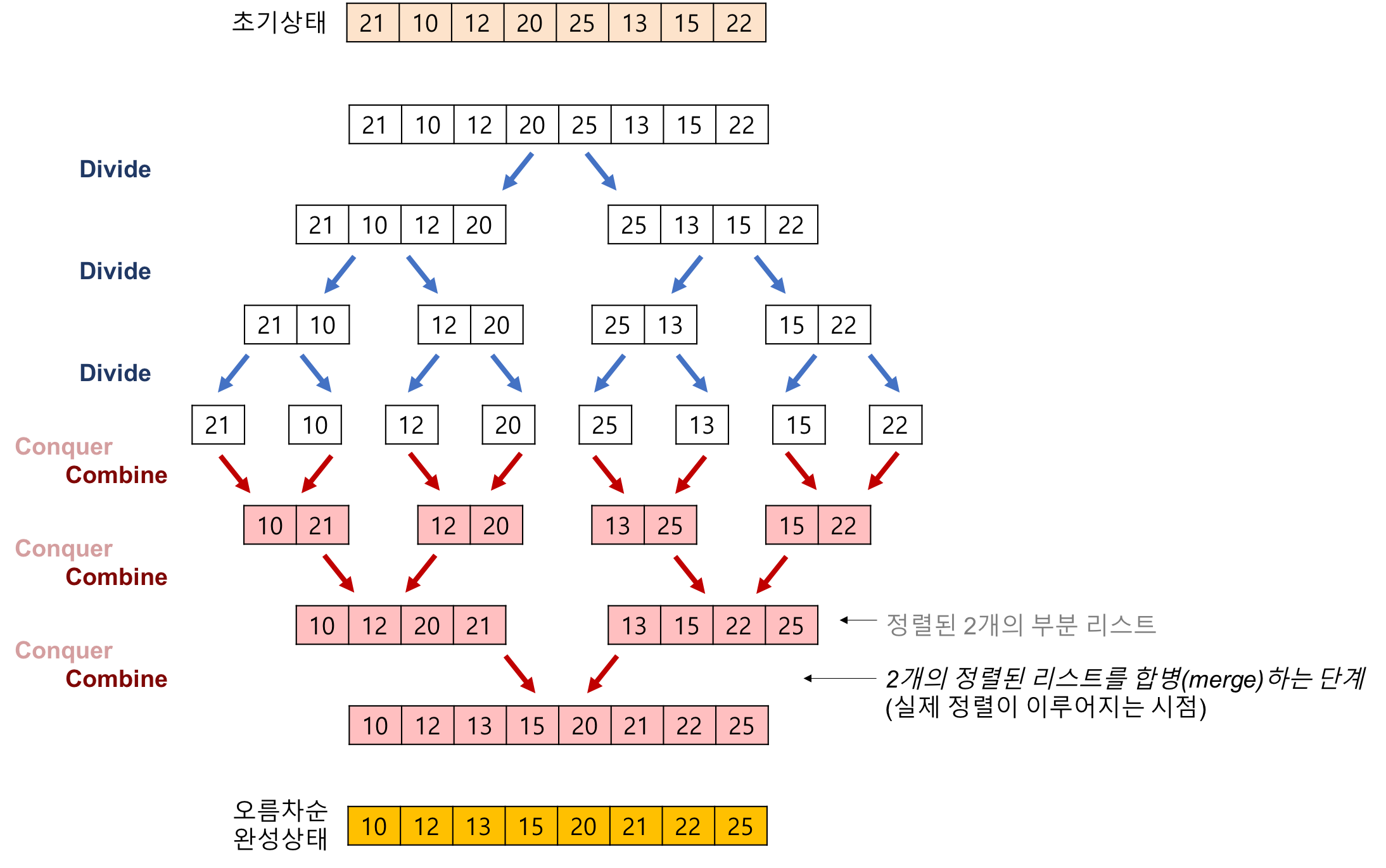
병합 정렬은 주어진 수열을 가운데에서 쪼개 비슷한 크기의 수열 두 개로 만든 뒤 이들을 재귀 호출을 이용해 각각 정렬한다.
그 후 정렬된 배열을 하나로 합침으로써 정렬된 전체 수열을 얻는 알고리즘이다.
특징
-
배열로 구현하게 되면, 값을 임시 저장할 임시 배열이 하나 더 필요하다.
데이터의 크기가 매우 커지면, 이동해야 하는 값이 많아지므로 매우 큰 시간 낭비를 초래한다.
그러나,Linked List를 이용하면 인덱스만 변경되므로 데이터의 이동이 무시할 만큼 작아진다. -
입력되는 데이터가 무엇이든 간에 정렬되는 시간은 같다. 퀵 정렬 같은 경우 평균, 최악 등 데이터에 따라서 정렬되는 시간이 다르지만, 병합 정렬은 정렬되는 시간이 같아서 안정적이다.
코드
#include <iostream>
#define FASTIO ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
int sorted[1000001];
void merge(int arr[], int start, int mid, int end){
int arrindex = start;
int tmpindex = start;
int arr2index = mid+1;
while (arrindex <= mid && arr2index <= end){
if (arr[arrindex] <= arr[arr2index]){
sorted[tmpindex] = arr[arrindex];
arrindex++;
}
else{
sorted[tmpindex] = arr[arr2index];
arr2index++;
}
tmpindex++;
}
if(arrindex > mid){
while(arr2index <= end)
{
sorted[tmpindex] = arr[arr2index];
arr2index++;
tmpindex++;
}
}
else
{
while(arrindex <=mid){
sorted[tmpindex] = arr[arrindex];
arrindex++;
tmpindex++;
}
}
for (int i = start; i<=end; i++)
arr[i] = sorted[i];
}
void merge_sort(int arr[], int start, int end){
if (start >= end)
return;
int mid = (start + end) / 2;
merge_sort(arr,start,mid);
merge_sort(arr,mid+1,end);
merge(arr,start,mid,end);
}
int main(){
int N;
cin >> N;
int array[N];
for(int i = 0; i<N; i++)
cin >> array[i];
merge_sort(array,0,N-1);
for(int i = 0; i<N; i++)
cout << array[i] << '\n';
}시간 복잡도
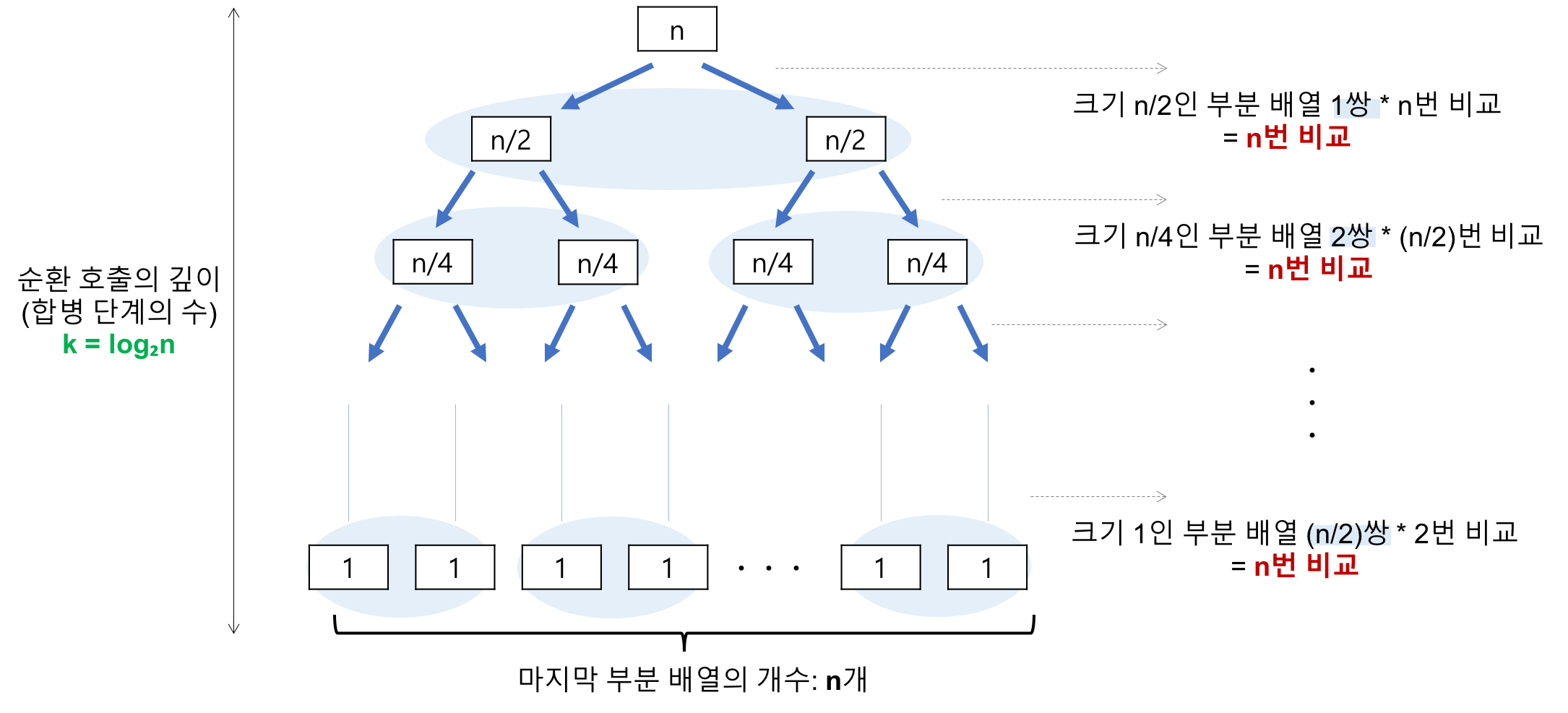
정렬된 두 부분 수열을 합치는 데는 두 수열의 길이 합만큼 반복문을 수행해야 하기 때문에, 병합 정렬의 수행 시간은 이 병합 과정에 달려있다.
아래 단계로 내려갈 수록 문제의 수는 2배가 되지만, 문제의 크기는 반으로 줄어드므로 한 단게 내에서 병합에 필요한 총 시간은 O(n)으로 항상 일정하다.
그리고 각 단계를 나타내는 가로줄에 있는 원소의 수는 항상 일정하므로 단계 수에 n을 곱하면 원하는 시간을 얻을 수 있다.
문제의 크기는 항상 거의 절반으로 나뉘기 때문에 필요한 단계의 수는 O(logN)이고, 따라서 시간 복잡도는
O(NlogN)이다.
참고 자료
https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
https://data-make.tistory.com/232
