import java.io.*;
import java.math.BigInteger;

class Main {
    static final BigInteger MOD = BigInteger.valueOf(1000000007);

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        long n = Long.parseLong(br.readLine());

        if (n == 0) {
            System.out.println(0);
        } else {
            BigInteger[][] result = fibMatrixPower(n - 1);
            System.out.println(result[0][0]);
        }
    }

    static BigInteger[][] fibMatrixPower(long n) {
        BigInteger[][] result = {{BigInteger.ONE, BigInteger.ZERO}, {BigInteger.ZERO, BigInteger.ONE}};
        BigInteger[][] base = {{BigInteger.ONE, BigInteger.ONE}, {BigInteger.ONE, BigInteger.ZERO}};

        while (n > 0) {
            if (n % 2 == 1) {
                result = multiplyMatrix(result, base);
            }
            base = multiplyMatrix(base, base);
            n /= 2;
        }

        return result;
    }

    static BigInteger[][] multiplyMatrix(BigInteger[][] a, BigInteger[][] b) {
        BigInteger[][] c = new BigInteger[2][2];
        c[0][0] = a[0][0].multiply(b[0][0]).add(a[0][1].multiply(b[1][0])).mod(MOD);
        c[0][1] = a[0][0].multiply(b[0][1]).add(a[0][1].multiply(b[1][1])).mod(MOD);
        c[1][0] = a[1][0].multiply(b[0][0]).add(a[1][1].multiply(b[1][0])).mod(MOD);
        c[1][1] = a[1][0].multiply(b[0][1]).add(a[1][1].multiply(b[1][1])).mod(MOD);
        return c;
    }
}

이거 정답 안 보고 어떻게 푸냐? 솔직히 여기서 행렬 떠올려서 분할 정복 떠올린 사람 있겠어?

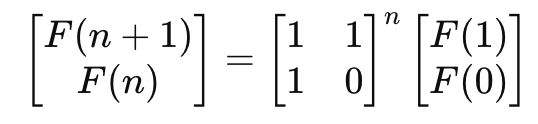
이걸 푸는 문제인데 이런 타입의 행렬을 푸는 접근법은 크게 2가지가 있다.

방법1

컴퓨터가 풀어줘

위에 올린 풀이가 그것인데 우선 문제의 n이 너무 크기 때문에 시간 복잡도가 로그인 알고리즘을 이용해야한다. 그게 분할정복인것이고

풀이는 단순하다. 2씩 나누면서 분할 정복해서 효과적으로 푼다.

이 풀이의 단점 시간 복잡도 대신 공간 복잡도를 희생하는 방법이다.

문제에서 입력 n이 너무 크면 당연히 시간복잡도가 로그인 알고리즘을 고려해야한다.

대신 그 알고리즘은 무조건 공간 복잡도를 희생할 수 밖에 없고

위 알고리즘도 재귀방식이라 공간복잡도가 크다.

방법2

정통적인 선형대수의 아이디어를 이용하는 것이다.

이런류의 문제는 선형대수에서 분해(decomposition)을 이용해서 푼다.

특이값분해, 대각화, 조드당 등등

분해는 이런 계산 쉽게 할려고 이용하는 방법이다.

이 문제 대각화가 가능하니 대각화로 접근해보면

고윳값과 고유벡터를 이용해야하는 데 아는 사람을 알거다. 모르면 검색하도록

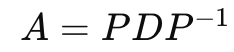
대각화가 가능하니까 위 식대로 구해주면

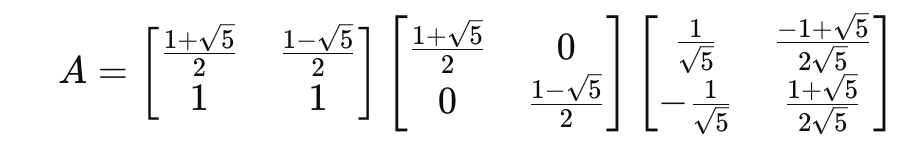
위처럼 피보나치 수열의 대각화를 구할 수 있다.

이거 왜 하냐?

A의 제곱을 구할 때 양옆에 역함수와 함수를 곱하니

직접 곱해보면 위 사실을 알 수 있다.

그리고 아주 좋은 소식은 D가 대각 행렬이다. 즉 곱셈이 아주 쉽다.

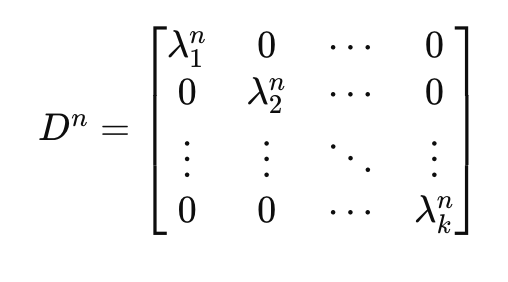
그냥 각 성분을 제곱해주면 되는 데 왜 이 식을 이용하지 않을까?

이 문제에선 아주 치명적인 단점이 있다.

대각화한 값이 실수라 부동 소수점 문제가 발생한다는 점.

컴퓨터로는 아마 정수가 아닌 근사값만 구할 수 있을것이다.

따라서 위 문제는 분할 정복으로 푸는 게 맞다. 다만 백준이 아닌 데이터 사이언스와 같은 다른 분야에선 고윳값이나 특이값을 통해 특징을 아는 게 중요하므로 위 방법도 고려하는 게 좋다.

결론

알고리즘 문제로 나오면 그냥 분할 정복으로 풀자.