프로그래머스 - 최대공약수와 최소공배수 (java)

class Solution {
    public int[] solution(int n, int m) {
        int[] answer = new int[2];
        int a = n;
        int b = m;
        while(b != 0) {
            int temp = b;
            b = a % b;
            a = temp;
        }
        answer[0] = a;
        answer[1] = (n * m) / a;
        return answer;
    }
}

최대공약수와 최소공배수를 그냥 구현 할려면 대체로 비효율적인 알고리즘일 것 이다. 최대공약수와 최소공배수 알고리즘은 그냥 유클리드 호제법을 이용한 위 알고리즘을 외우는 게 좋다.
a, b의 최대공약수를 구하는 문제에서 a가 b보다 클 때 r을 a % b = r이라고 하자.
(a, b)를 a와 b의 최대공약수라고 했을 때 (a, b) = (b, r)를 이용해서 문제를 풀자.
유클리드 호제법에 재귀를 이용하는 경우가 많은데 재귀보단 위 알고리즘이 공간복잡도가 효율적이다.
최소 공배수는 다음과 같은 사실로 구할 수 있다.

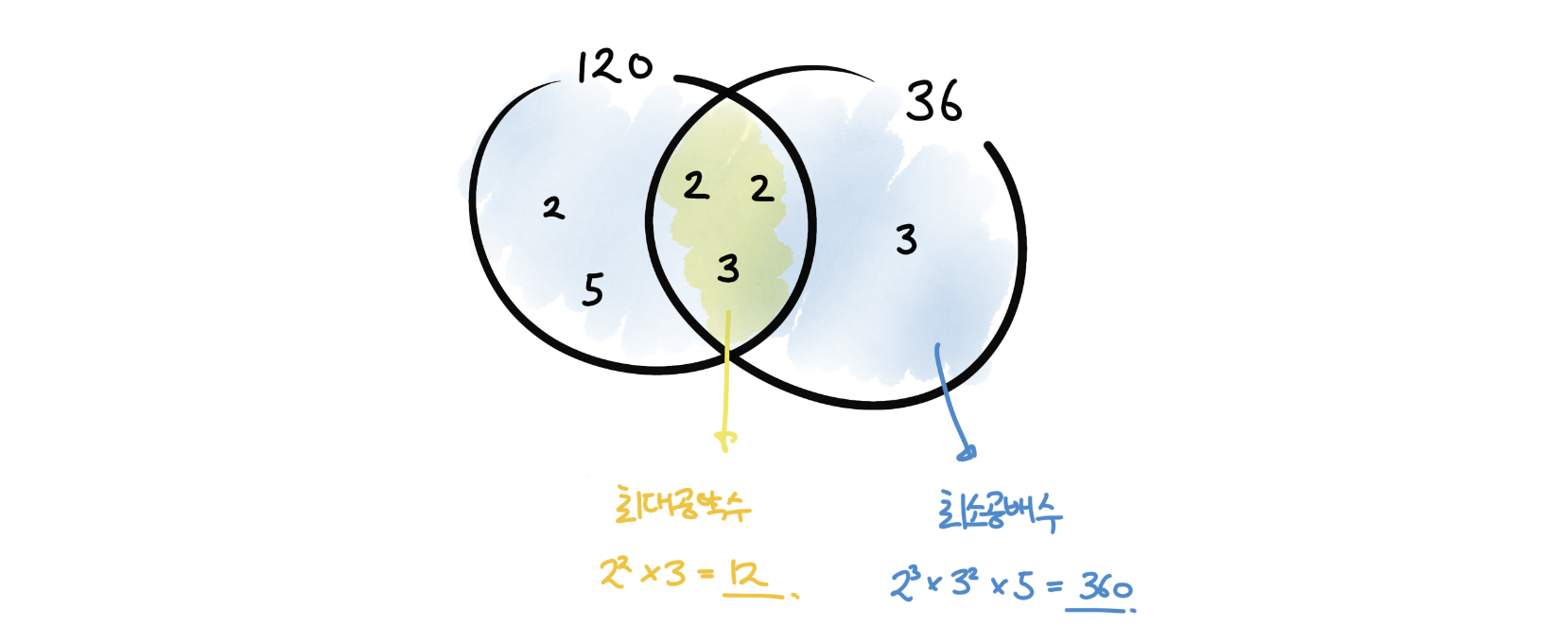
그림 출처: https://dimenchoi.tistory.com/46