코테 개념 모음집

유클리드 호제법

유클리드 호제법 : GCD(num1, num2) = GCD(num2, num1 % num2)

최대공약수, 최소공배수

const solution = (num1, num2) => {
  // 최대 공약수
  const gcd = (a, b) => (a % b === 0 ? b : gcd(b, a % b));
  // 최소 공배수
  const lcm = (a, b) => (a * b) / gcd(a, b);
  return [gcd(num1, num2), lcm(num1, num2)];
};

최빈값

프로그래머스 최반값 구하기

function solution(array) {
    let obj = {} // key : 값, value : 갯수
    array.forEach((item) => {
        if (obj[item]) {
          obj[item] += 1;
        } else {
          obj[item] = 1;
        }
    });
    
    let countList = [] // 갯수들만 모아둔 배열
    let modeValue = obj[Object.keys(obj)[0]]; // 갯수
    let modeKey = Object.keys(obj)[0]; // 값

    for (const item in obj) {
        countList.push(obj[item])

        if (obj[item] > modeValue) {
          modeKey = item;
          modeValue = obj[item];
        }
    }
          
    countList.sort((a,b) => b-a);
    if(countList[0] === countList[1]) return -1 // 최빈값이 여러개일때
        
    return Number(modeKey);

}

조합

서로 다른 n개 중 r개를 뽑는데 순서가 없으며 같은 것을 중복해서 뽑지 않을때 조합을 이용한다.

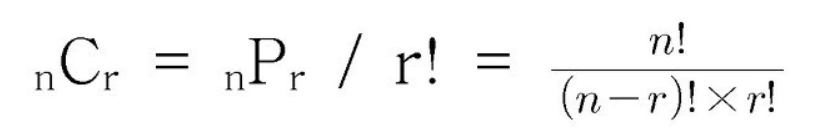
const factorial = (num) => {
    let returnFactorial = BigInt(1)
    for(let i = num; i >= 1; i-- ) {
        returnFactorial*=BigInt(i)
    }
    return returnFactorial
}

const solution = (n, r) => {
    return factorial(n) / (factorial((n-r)) * factorial(r))
}

소인수분해

n의 소인수들을 중복 없이 배열로 반환

const solution = (n) => {
    let i = 2;
    let primes = []
    
    while (i <= n) {
      if (n % i === 0) {
        n = n / i
        primes.push(i)
        i = 1;
      }
        i++;    
    }
    
    return Array.from(new Set(primes)) // 중복제거
}

소수 찾기

2,3,5,7,11 ... 등 1과 자기 자신으로만 나누어지는 떨어지는 수

const isPrimeNumber = (number) => {
  if (number <= 1) return false;

  for (let i = 2; i <= Math.sqrt(number); i++) {
    if (number % i === 0) {
      return false;
    }
  }
  return true;
};