Abstract
train에 stability를 비약적으로 향상
loss값이 작아짐에따라 비례해서 성능이 좋아짐
기존 GAN의 discriminator 대신 Critic 사용 -> 0~1사이의 확률값으로 T/F를 판단하는 것이 아닌 scoring을 통해 T/F판단
architecture와 hyperparameter에 덜 민감 -> 학습 편리
learning signal 알기쉬움
Model
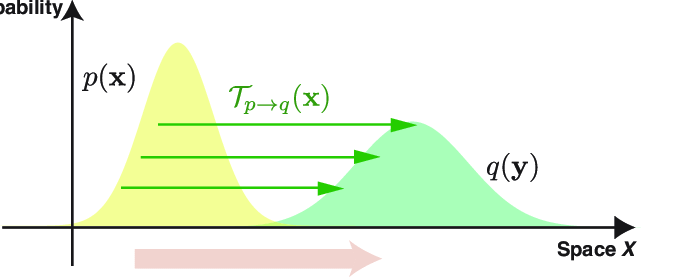
Wasserstein distance
(reference www.researchgate.net)
교환법칙 성립하는 matrix로 earth mover's distance(EM distance) 라고도 한다.
-> 토양을 한쪽에서 다른쪽으로 옮긴다는 의미를 가진다
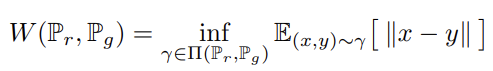
수식으로 보면 다음과 같다.
inf 기호는 하한중에 가장 큰 값을 의미하는 minimum이라고 보면 된다.
Γ는 두 분포에서 만들어 낼 수 있는 모든 joint 조합을 의미한다. -> intractable -> neural net training
-> 즉 x로부터 y를 얼마나 옮겨야 하나를 나타내는 척도이다.
Wasserstein distance가 JS distance보다 두 분포 사이의 거리를 나타낼 때 왜 더 유용한가?
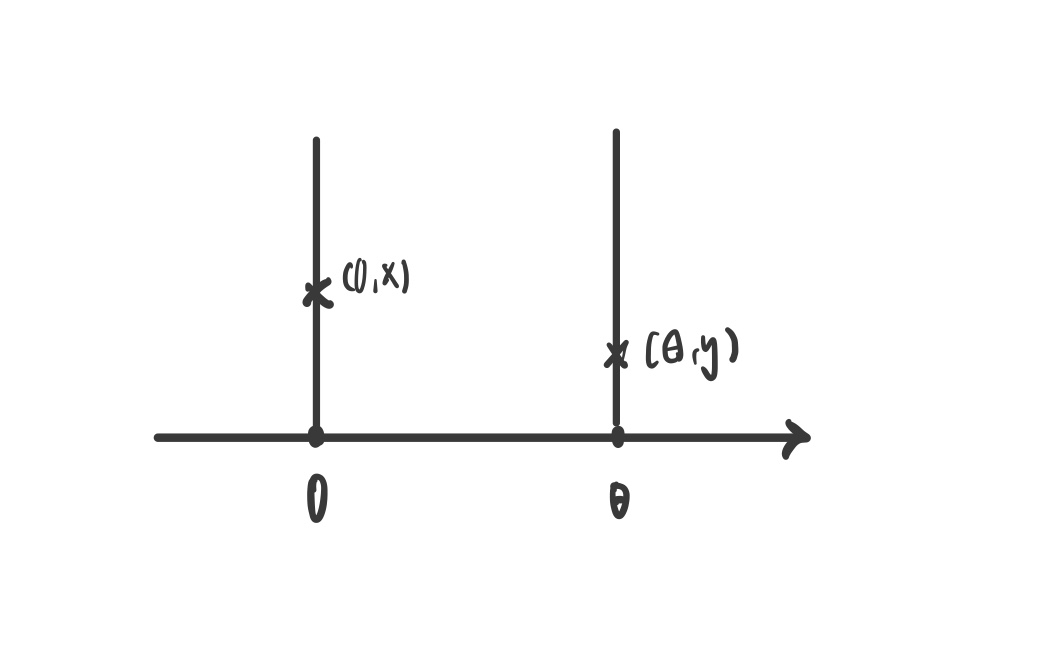
예를 들어 두 분포가 다음과 같다고 할 때 두 분포의 높이가 같을 때 최솟값 θ을 가짐
이를 그래프로 표현하면
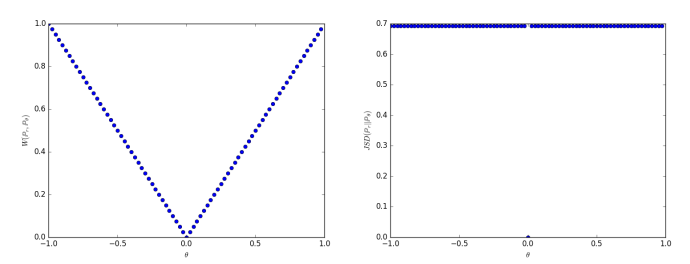
왼쪽 그래프와 같다.
이 그래프는 연속이므로 좀 더 학습에 도움이 되는 gradient를 가진다.
반면에 오른쪽 그래프는 기존 GAN에서 사용하던 JS distance인데 이는 극단적인 값을 가지고 미분 값이 0이기 때문에 학습에 잘 도움이 되지 못한다.
Loss
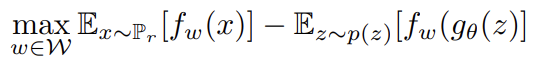
loss 수식은 기존의 GAN loss와 비슷한데 여기서 f는 critic을 의미한다.
x는 real 분포이고 z는 노이즈이다.
즉 f가 real분포의 score값은 높이고 fake분포의 score값은 낮춤으로써 둘 사이의 차이를 maximize 하는 것이 목적이다.
Algorithm

여기서 주목할 부분은 weight clipping이다.
이는 weight 값이 너무 크거나 너무 작은 값을 조절한다.
본 논문에서의 threshold는 [-0.01, 0.01]
그리나 clipping하는 것은 인위적이기 때문에 개선의 여지가 있다.
그래서 이를 개선한 것이 WGAN-GP: WGAN with gradient penalty이다.
critic loss에 regularizer term을 추가
gradient의 norm에 패널티를 부여 norm penalty 처럼
critic loss에 regularizer term을 추가
