그래프를 탐색하는 방법인 DFS와 BFS에 대해 알아보자
깊이 우선 탐색 (DFS)
DFS약자를 풀어서 보면 depth first search 깊이 우선 탐색이다.
한 정점에서 시작해서 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면!! 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 아직 방문하지 않은 정점을 다른 방향으로 탐색하는 방법이다.
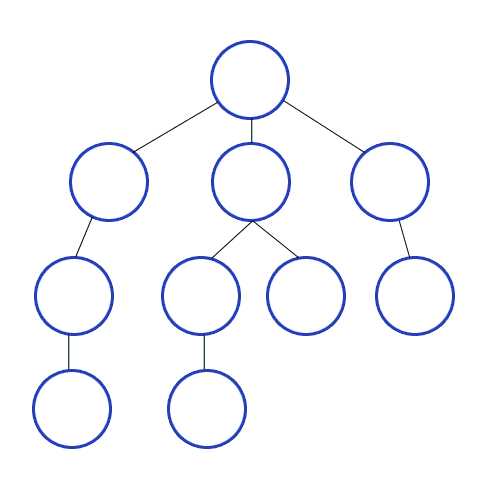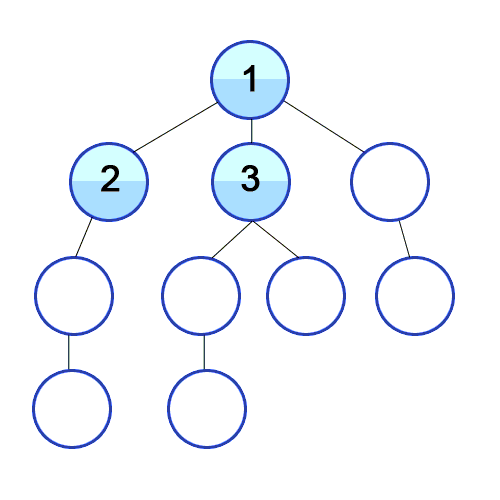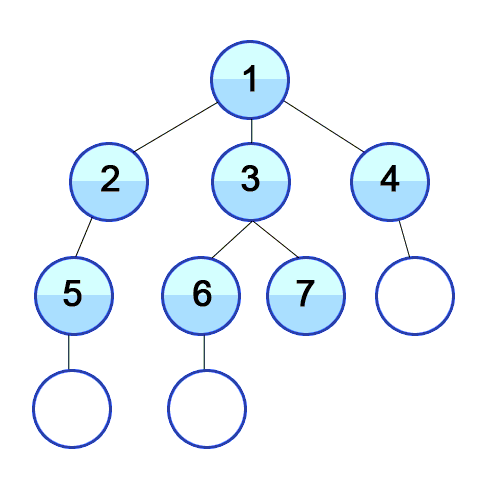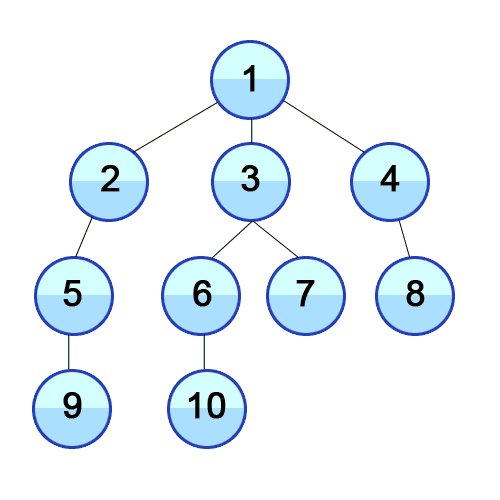
그래프로 표현해보면 아래와 같다.
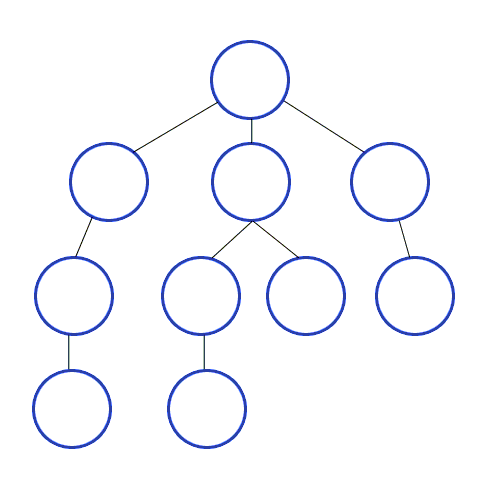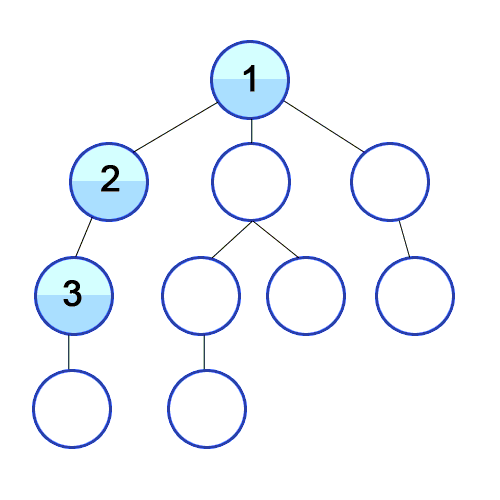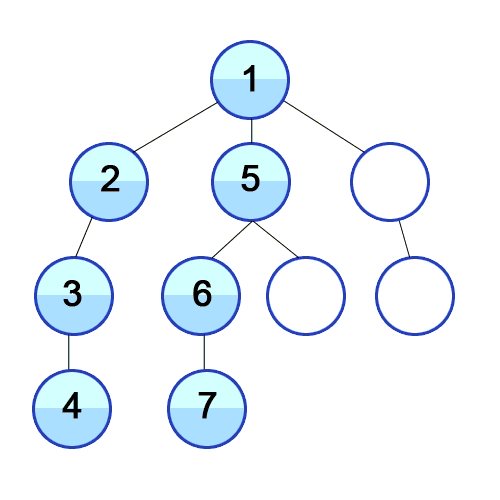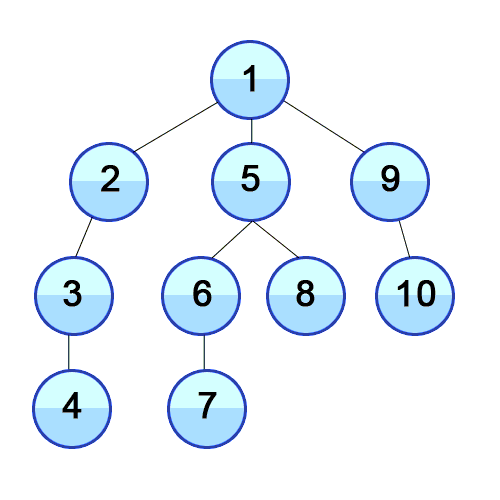
출처 https://ko.wikipedia.org/wiki/깊이_우선_탐색
모든 정점을 방문하고자 하는 경우 이 방법을 선택! 하지만 BFS보다 느리다.
1. 스택을 이용하여 갈 수 있을 때까지 최대한 많이가고
2. 갈 수 없으면 이전 정점으로 돌아간다.
!!! 여기서 어떤 정점을 방문했었는지 여부를 반드시 검사 해야 한다. (검사하지 않아서 무한루프에 빠진 경험이 .......) 스택에 넣었을 때 방문했다고 체크하면 된다.
코드를 통해 살펴보면
위와같이 스택 말고도 재귀함수를 사용해 문제를 해결하는 경우도 있다.
바로 코드를 통해 살펴보면
재귀함수를 사용한 문제가 더 복잡한 문제여서 코드가 더 길다. 하지만 재귀함수를 사용하는 것이 더 간단하고 check배열을 사용할 필요가 없어 스택보다 재귀함수를 더 자주 이용한다.
넓이 우선 탐색 (BFS)
BFS약자를 풀어서 보면 breach first search 넓이 우선 탐색이다.
한 정점에서 시작해서 인접한 정점을 모두 방문한다음 첫 번째로 연결 된 정점으로 가서 그것과 연결된 정점들을 방문하고 다음으로 나머지 정점들을 방문하여 동일한 동작을 반복하는 방법이다.
그래프로 표현해보면 아래와 같다.
출처 https://ko.wikipedia.org/wiki/넓이_우선_탐색
두 정점사이에 최단경로를 찾고자 할 때 이 방법을 선택!
1. 큐를 이용하여 현재 정점에서 인접한 정점을 모두 큐에 넣는다.
2. 넣은 정점을 하나씩 꺼내서 동일한 동작을 반복한다.
!!! 여기서도 어떤 정점을 방문했었는지 여부를 반드시 검사 해야 한다. bfs는 재귀적으로 동작하지 않음
코드를 통해 살펴보자
#정리
모든 정점을 방문해야하는 문제, 경로의 특징을 저장해야 하는 문제 -> DFS
최단경로를 구해야 하는 문제 -> BFS
응애