03-1. k-최근접 이웃 회귀
🔈 회귀 (Regression)
- 지도 학습 알고리즘은 크게 분류와 회귀로 나뉜다.
- 분류 : 샘플을 몇 개의 클래스 중 하나로 분류하는 문제
- 회귀 : 클래스 중 하나로 분류하는 것이 아닌 임의의 어떤 숫자를 예측하는 문제.
따라서 타깃값이 가상으로 만든 코드값이 아닌 임의의 수치이다.
k-최근접 이웃 회귀
- k-최근접 이웃 알고리즘을 사용해 회귀 문제를 푼다.
- 예측하려는 샘플에 가장 가까운 이웃 샘플을 찾고 이 샘플들의 타깃값을 평균값을 구해 예측으로 삼는다.
🔧 데이터 준비
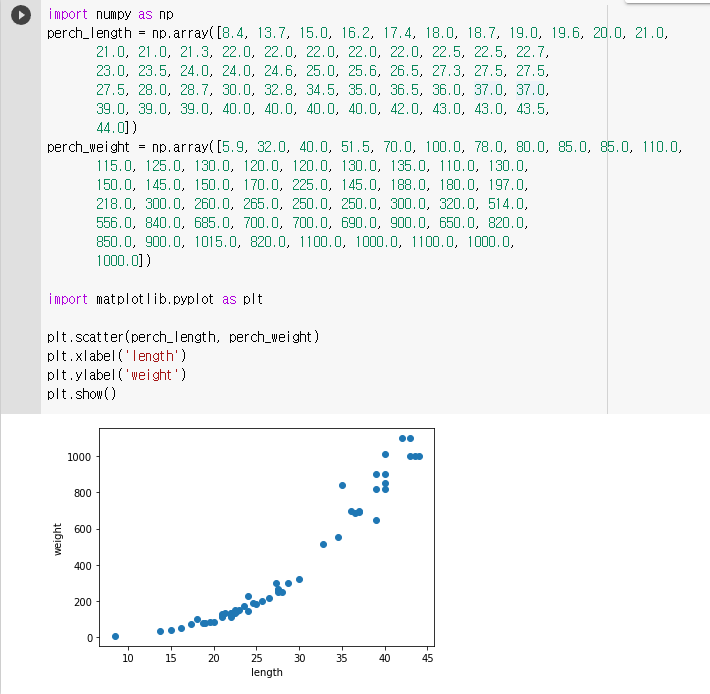
🔧 훈련 세트 준비

KNeighborsRegressor
- 사이킷런에서 k-최근접 이웃 회귀 알고리즘을 구현한 클래스
- 객체를 생성하고 fit() 메서드로 회귀 모델을 훈련할 수 있다.
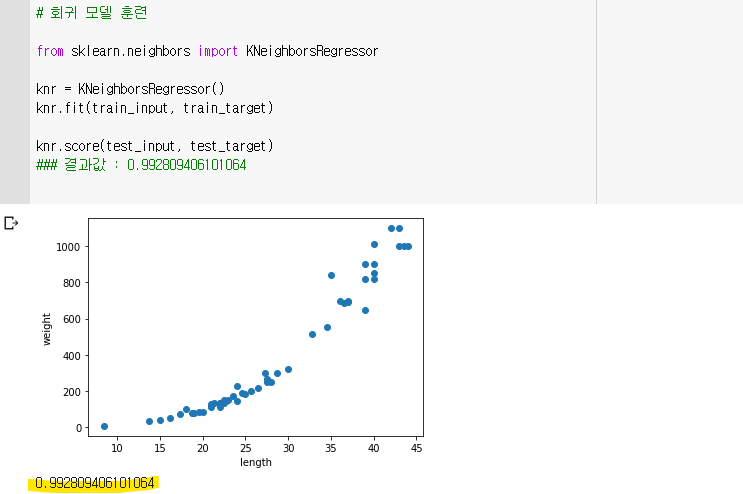
🔧 테스트 세트 점수
🔈 분류와 회귀 모델을 평가하는 방법
- 정확도 : 분류를 평가하는 방법. 테스트 세트에 있는 샘플을 정확하게 분류한 개수의 비율
- 회귀에서는 정확한 숫자를 맞히는 게 거의 불가능하므로 결정계수라는 값으로 평가한다
결정계수(R²)
- 대표적인 회귀 문제의 성능 측정 도구. 1에 가까울수록 좋고, 0에 가깝다면 성능이 나쁜 모델
- 예측이 평균과 비슷해지면 분모와 분자의 값이 비슷해져 R²는 0에 가까워진다.
- 예측이 타깃을 정확히 맞춘다면 분자가 0에 가까워져 R²는 1에 가까운 값이 된다.


사진출처 : https://velog.io/@arittung/DeepLearningStudyDay4, https://adamlee.tistory.com/entry/%EC%89%AC%EC%9A%B4-%EC%84%A4%EB%AA%85%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EA%B2%B0%EC%A0%95%EA%B3%84%EC%88%98R2-%EB%9C%BB-%EC%A6%9D%EB%AA%85
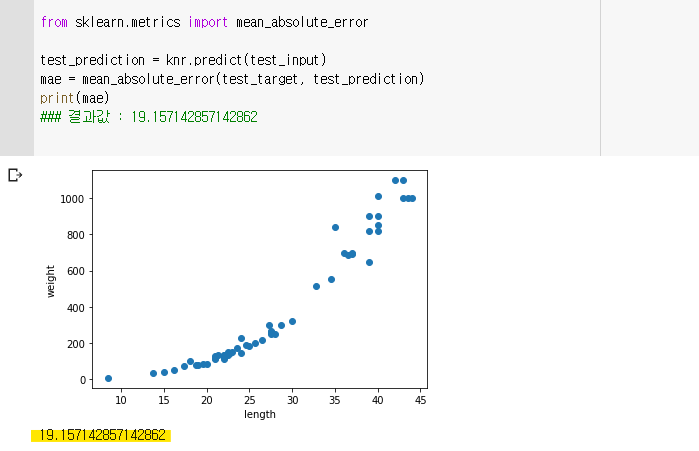
🔧 mean_absolute_error
- 타깃과 예측의 절댓값 오차를 평균하여 반환한 것
- mean_absolute_error 을 통해 결정계수(R²) 보다 직관적인 값을 얻을 수 있다.
🔈 과대적합과 과소적합

사진출처 : https://youtu.be/0mrLRkgbjA0
-
훈련 점수보다 테스트 점수가 낮게 나오는 것이 일반적이다.
-
이런 현상을 훈련세트를 적절히 학습하지 못한 과소적합이라고 한다.
-
위 사진과 반대로 훈련세트에는 0.99와 같은 높은 성능을 보이면서 테스트세트에는 0.6과 같이 형편없는 결과가 나온 경우, 실전에서는 형편없어지는 과대적합 현상이 발생한다.
과대적합 (overfitting)
- 모델의 훈련 세트 성능이 테스트 세트 성능보다 훨씬 높을 때 일어난다.
- 모델이 훈련 세트에 너무 집착해서 데이터에 내재된 거시적인 패턴을 감지하지 못한다.
과소적합 (underfitting)
- 훈련 세트와 테스트 세트 성능이 모두 동일하게 낮거나 테스트 세트 성능이 오히려 더 높을 때 일어난다.
- 이런 경우 더 복잡한 모델을 사용해 훈련 세트에 잘 맞는 모델을 만들어야 한다.
🔧 이웃 개수 줄이기
- 이웃의 개수를 5에서 3으로 줄임으로써 더 적합한 결과를 얻어낼 수 있었다.
- 이웃의 개수를 줄일수록 샘플 하나하나와 과하게 유사한 과대적합이 발생하고
- 이웃의 개수를 늘릴 수록 훈련세트 성능이 낮은 (훈련세트를 제대로 훈련하지 못한) 과소적합이 발생한다.

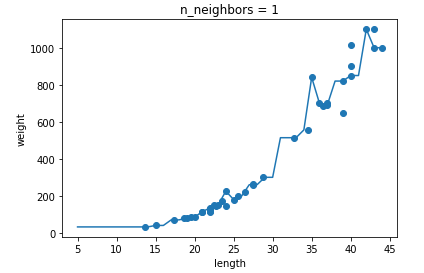
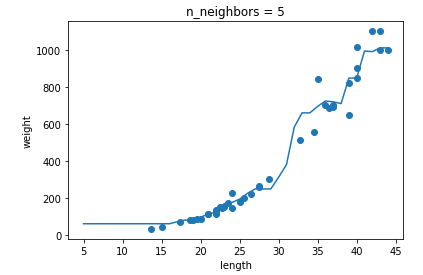
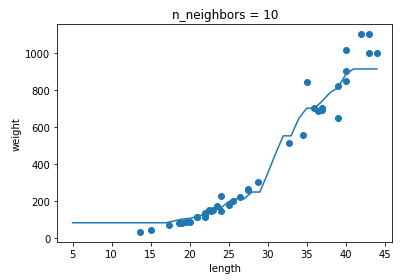
🎉 기본미션 - 확인문제 2
과대적합과 과소적합에 대한 이해를 돕기 위해 복잡한 모델과 단순한 모델을 만들겠습니다. 앞서 만든 k-최근접 이웃 회귀 모델의 k값을 1, 5, 10으로 바꿔가며 훈련해 보세요. 그다음 농어의 길이를 5에서 45까지 바꿔가며 예측을 만들어 그래프로 나타내 보세요. n이 커짐에 따라 모델이 단순해지는 것을 볼 수 있나요?
- n이 커짐에 따라 각 샘플의 영향이 줄어드는 것을 확인 할 수 있었다.
03-2. 선형회귀
🔈 선형회귀
- 특성과 타깃 사이의 관계를 가장 잘 나타내는 선형 방정식을 찾는 것
- 특성이 하나면 직선 방정식이 된다.
- 선형 회귀가 찾은 특성과 타깃 사이의 관계는 선형 방정식의 계수 또는 가중치에 저장된다.
- 머신러닝에서 종종 가중치는 방정식의 기울기와 절편을 모두 의미하는 경우가 많다.
🔧 LinearRegression

- 직선을 구하기 위해서는 기울기와 절편이 필요하다.
- 이는 직선형태인 선형회귀도 마찬가지인데 이를 LinearRegression 클래스를 통해 구할 수 있다.
lr = LinearRegression() 로 선언했을 때
- 기울기(coefficient) : lr.coef_
- 절편 : lr.intercept_
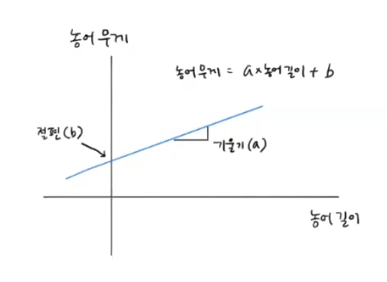
사진 출처 : https://youtu.be/xkknXJeEaVA
🔈 모델 파라미터
- 머신러닝 알고리즘이 찾은 값
- 선형 회귀가 찾은 가중치(기울기, 절편)처럼 머신러닝 모델이 특성에서 학습한 파라미터를 말한다.
- 많은 머신러닝 알고리즘의 훈련 과정은 최적의 모델 파라미터를 찾는 것
- 이를 모델 기반 학습이라고 부른다.
🎉 선택미션 - 모델 파라미터란?
머신러닝 알고리즘이 찾은 값으로
선형회귀의 가중치(기울기, 절편)와 같이 머신러닝 모델이 특성에서 학습한 파라미터를 뜻한다.
머신러닝은 이 모델 파라미터의 최적값을 찾기위해 계속 훈련하는 것이다.
🔈 다항 회귀
- 다항식을 사용하여 특성과 타깃 사이의 관계를 나타낸다.
- 이 함수는 비선형일 수 있지만 여전히 선형 회귀로 표현할 수 있다.
후기
- 시간이 부족해 중간부터 강의 없이 급하게 학습했더니 실습이 부족해 아쉽다.
- 복습하고 다음 주차도 무리없이 진행하는 것이 목표!!
- 책 실습과 유튜브강의가 너무 잘되어 있다고 생각한다. 덕분에 스트레스 없이 아주 편하게 학습중이다.