이 글은 투빅스에서 정리해주신 이 글과 제가 들은 수업(AI506)을 바탕으로 정리한 내용입니다. 잘못된 부분이 있다면 soyoung.cho@kaist.ac.kr로 메일 부탁드립니다.
들어가기
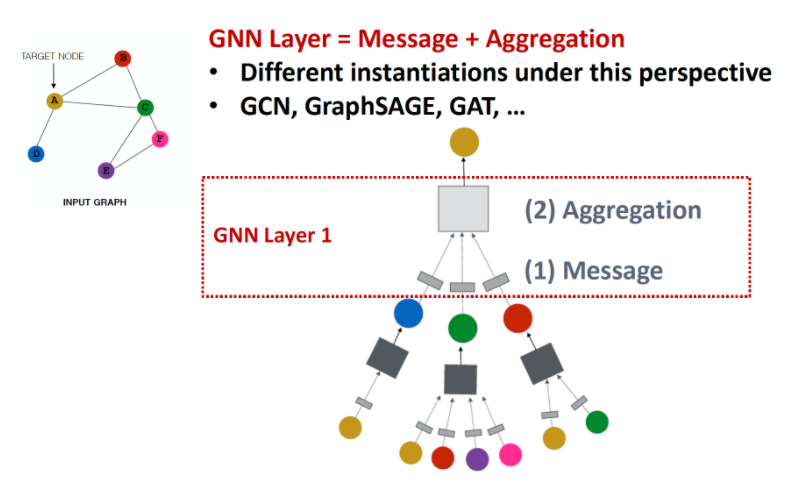
그래프에서 노드의 정보를 어떻게 임베딩 하는 것이 관건인데, Convolution 하듯 노드는 각자 이웃 노드들의 정보를 모아 Neural Network를 적용할 수 있습니다.
Simple Neighbor aggregation

정보가 전달되어 embedding 값을 가지게 되는 과정을 수식적으로 표현하면 위와 같습니다. 여기서 학습 가능한 것은 와 인데요, 행렬은 이웃 노드들의 이전 레이어에서의 embedding 값 평균에 대한 가중치 행렬이고, 행렬은 노드 v의 이전 레이어에서의 embedding 값에 대한 가중치 행렬입니다. 즉 은 neighbor에 대한 가중치, 는 self에 대한 가중치이죠. 이 설명을 그림으로 나타낸 것이 아래 그림입니다.
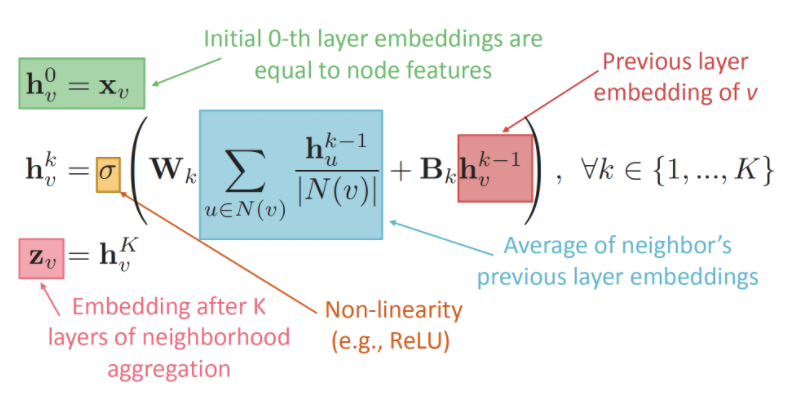
이제 위 수식을 기본 neighbor aggregation 방식이라 부르고, 다른 GNN 알고리즘과의 차이를 간단히 비교해보겠습니다.
Graph Convolutional Networks (GCN)
GCN의 핵심은, 노드 v의 이웃 노드들과(neighbor) 자기 자신(self) 모두에 대해 동일한 파라미터인 를 사용한다는 것입니다. 위에서의 neighbor aggregation 방식과 비교해보면 다음과 같습니다.

위의 수식이 위에서 말한 기본 neighbor aggregation 방식이고, 밑이 GCN 방식입니다. 가장 두드러지는 차이점은 자기 자신 노드 v의 이전 레이어에서의 embedding 값에 대한 가중치 행렬 이 GCN에는 없다는 것입니다. 노드 v와 v의 이웃 노드들이 동일한 가중치 행렬 를 사용하고 있다는 것이 큰 차이점입니다. 또한, 기본 neighbor aggregation 방식에서는 노드 v의 Degree로 나누어 normalize를 해주었던 반면, GCN에서는 분홍색 화살표 부분을 보면 알 수 있듯 노드 v의 Degree와 이웃 노드 각각의 Degree를 곱한 값으로 나누어 normalize를 진행합니다.
이렇게 한 결과 우수한 성능을 보였다고 하는데요, 성능이 우수한 이유가 무엇일까요?
- More parameter sharing
- 임베딩 값을 구하는 노드(v)와 이웃 노드들 간의 가중치 행렬을 구분하지 않고 공유한 것이 성능 향상의 요인이 된다고 합니다.
- Down-weights high degree neighbors
- 이웃 노드 중 degree가 컸던, 즉 연결된 노드가 많은 인싸(?) 노드에 대한 embedding 값을 적게 반영합니다. 다시 말해 degree가 큰 이웃 노드에 대해 penalty를 주었다고 해석 할 수 있을 것 같네요.
GraphSAGE
다음 GraphSAGE입니다. GraphSAGE는 쉽게 말해, 노드와 이웃 노드들의 가중치 값을 더하지 않고 concat하는 것이 큰 차이입니다. 이번에도 위에서의 기본 neighbor aggregation 방식과 비교해보겠습니다.
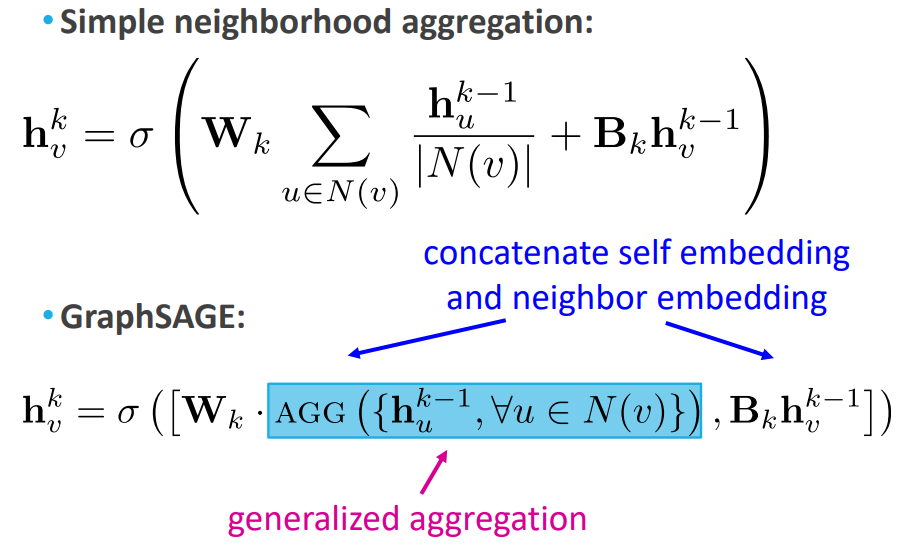
위의 수식이 기본 neighbor aggregation 방식이고, 아래가 GraphSAGE입니다. 차이점은 다음과 같습니다. 첫째, 기본 neighborhood aggregation 방식의 부분이 GraphSAGE에서는 일반화된 Aggregation 함수로 나와 있습니다. 즉 이웃 노드의 임베딩을 구하는 수식이 약간 다를 수 있겠네요. 자세한건 아래에 더 기술하겠습니다. 둘째, self embedding과 neighbor aggregation add가 아닌 concat 되는 것입니다.
이 일반화된 Aggregation 함수에는 다음과 같은 공식이 올 수 있습니다.

- Mean 방식은 위 기본 neighborhood aggregation 방식과 동일하게 이웃 노드의 임베딩 값(message)을 평균 내는 것입니다.
- LSTM을 aggregation 함수로 사용하는 것이 흔하지는 않다고 합니다. 일반적으로는 mean, pool, sum을 더 사용합니다.
Graph Attention Network (GAT)
이전 모델들은(GCN, GraphSAGE) 각 이웃 노드의 중요도를 같다고 보았기 때문에 () unweighted graph를 가정했다고 볼 수 있습니다. GAT의 아이디어는 여기서 출발하는데요, 이웃 노드의 중요도를 모두 같다고 보지 않고 중요한 노드에 더 가중치를 주자는 것입니다. 이 가중치인 Edge weight은 가까운 이웃에 더 attention을 주는 방법으로 학습할 수 있습니다.
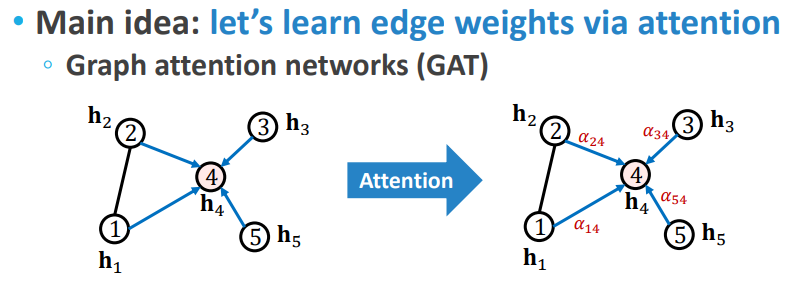
노드의 중요도를 모두 로 했던 다른 모델과 달리 GAT는 attention mechanism과 유사하게 attention coefficient를 구하고 softmax를 취해서 확률 값인 를 구하는 것입니다. 자세한 절차는 아래와 같습니다.

- Step 1. 각 노드의 에 가중치 행렬 W를 곱해 을 구합니다
- 는 neighbor aggregation 결과였습니다.
- 에 가중치 행렬 W를 곱하는 것은 Simple Neighbor aggregation, GCN, GraphSAGE에서도 동일하게 적용되는 연산이었습니다. 여기서 우리는 이 곱의 결과를 라고 표현하는 것일 뿐입니다.
- Step 2. 우리는 두 노드 간의 중요도를 파악하려고 하는 것이기에, 두 노드의 와 을 concat한 후 를 곱해 attention score를 구해줍니다. 이때의 도 학습가능한 파라미터 입니다.
- Step 3. Attention score들에 softmax를 취해 normalize합니다. 이렇게 나온 attention distribution 값을 이용해 노드의 중요도로 활용합니다. 아래 수식과 같습니다.
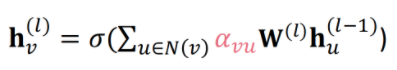
이전에는 를 모든 노드에 동일하게 노드 중요도 가중치로 사용했던 반면, GAT에서는 값을 이용해 노드별로 다르게 가중치를 주는 것입니다.
Multi-head Attention
트랜스포머의 multi-head 개념과 같이, attention을 계산하는 주체를 여러 개 두어 값을 여러개 도출할 수 있습니다. 나온 값들은 aggregate하여 최종 output 값을(neighbor aggregation 값) 계산할 수 있습니다.
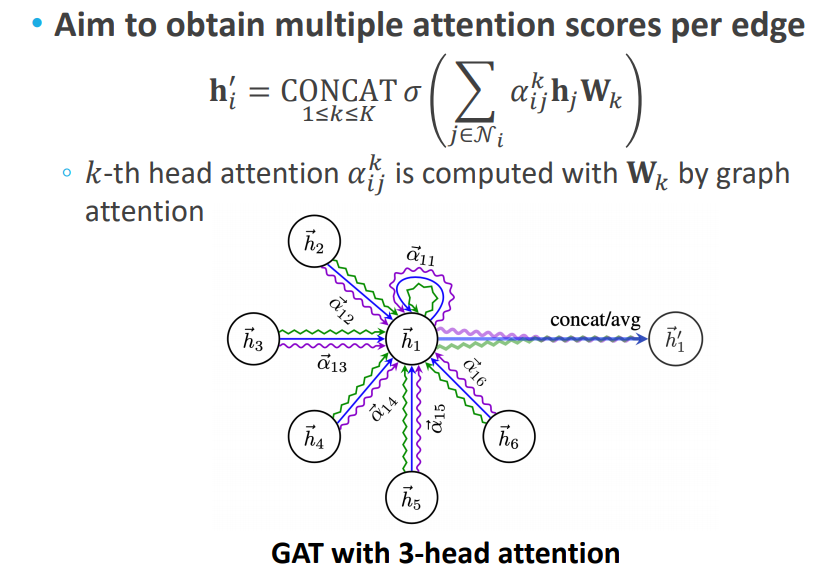
GAT를 제안한 논문에서는 GCN이나 GraphSAGE보다 우수한 성능을 보인다고 주장하는데요. 안타깝게도 다른 태스크에서는 그렇게 많이 쓰이지는 않는다고 합니다. 계산량이 많고, 느리기 때문에 GPU로 학습하기엔 적합하지 않다는 주장이 있다고 하네요.

만약 난수를 발생해서 학습에 사용하는 데이터셋을 생성 했다면 이 데이터셋에대한 타당성 검증은 어떻게 하나요?