
추천시스템은 SVD로부터 나와서 동일 알고리즘이 여러 이름을 가질 수 있습니다. 이전에 배운 추천 알고리즘(Matrix Factorization)은 이 SVD에서 나온 컨셉이고, 이번에 정리할 내용은 실제 SVD 알고리즘 그 자체에 대한 내용이라고 할 수 있습니다.
Dimentionality Reduction (차원 축소)
입력 데이터는 2차원인데 실제 effictive 차원은 1차원일 수 있습니다. 3차원 데이터의 effective 차원이 2차원일 수도 있구요.
행렬의 Rank
SVD는 랭크와 밀접한 관련이 있습니다. 행렬 A의 랭크란, A행렬의 선형 독립적 컬럼(행)의 개수입니다. 컬럼을 이용해 랭크를 정의할 수도 있고, 행을 이용해 랭크를 정의할 수도 있습니다. [[1, 2, 1], [-2, -3, 1], [3, 5, 0]]의 행렬이 있을 때, [3, 5, 0]는 [1, 2, 1] + [-2, -3, 1]와 같이 합으로 표현될 수 있기 때문에 본 행렬의 랭크는 2입니다. 이 기저벡터 [1, 2, 1]와 [-2, -3, 1]를 이용해 새로운 좌표들을 구할 수 있습니다.
따라서 우리는 [1,0,0], [0,1,0], [0,0,1] 이었던 기존의 기저 벡터 대신, 이 행렬을 새로운 기저벡터인 [1, 2, 1]와 [-2, -3, 1]를 이용해 2차원으로 표현할 수 있습니다.
차원 축소의 목적은 무엇일까요? 새로운 차원(축)을 찾는 것이 바로 차원축소의 목적이라고 할 수 있습니다. 그럼 차원을 축소하는 이유는 무엇일까요?
차원축소 이유
- 숨겨진 상관관계(correlation)과 토픽을 찾을 수 있습니다.
- 예를 들어, 같이 등장하는 단어들을 묶을 수 있죠.
- 중복되거나 노이지한 피처를 제거할 수 있습니다.
- 예를 들어, 모든 단어가 유용한 것은 아닐 것입니다.
- 해석, 시각화
- 데이터의 저장, 처리 용이
SVD 정의

U와 , V를 곱하여 입력 행렬을 표현할 수 있습니다. 다시 말해, 입력 행렬 A는 이 3가지 행렬로 분해될 수 있습니다.
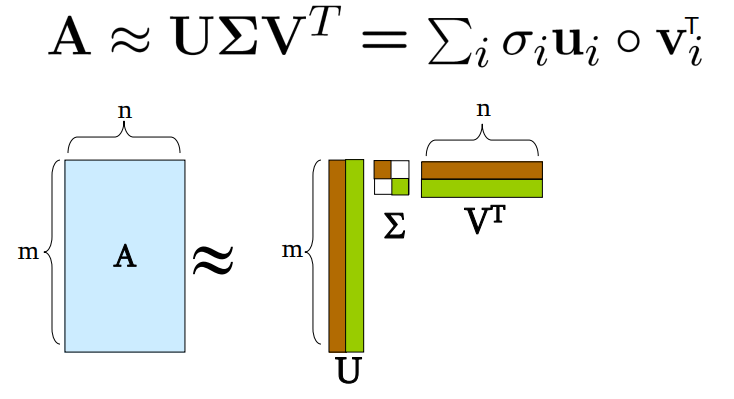
그림으로 표현하면 위와 같습니다. 입력행렬 A는 U와 , V로 분해가 되고, U의 열인 r은 랭크입니다. r는 m 혹은 n보다 작습니다. (r << m or n)
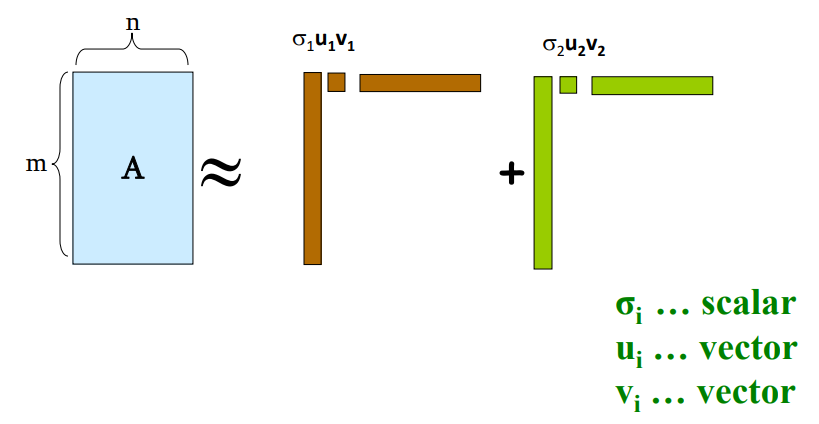
랭크가 2라면, 분해된 U, , V는 Rank 1 행렬과 Rank 2 행렬의 합으로 표현될 수 있습니다. 즉 각 열 r을 이용해 구해진 랭크 행렬의 합인 것이죠.
SVD의 속성

행렬 A에 대한 U,,V U의 열과 V의 열은 서로 직교입니다(orthonormal). orthonormal = orthogonal + normal. (1) U와 V의 열이 서로 직교하고 (2) 가 diagonal 하다면 (대각행렬) 행렬 A에 대한 U,,V는 유일하다고 합니다(unique). (잘 이해한 것인지 모르겠습니다 ㅠㅠ)
예) 유저 - 영화

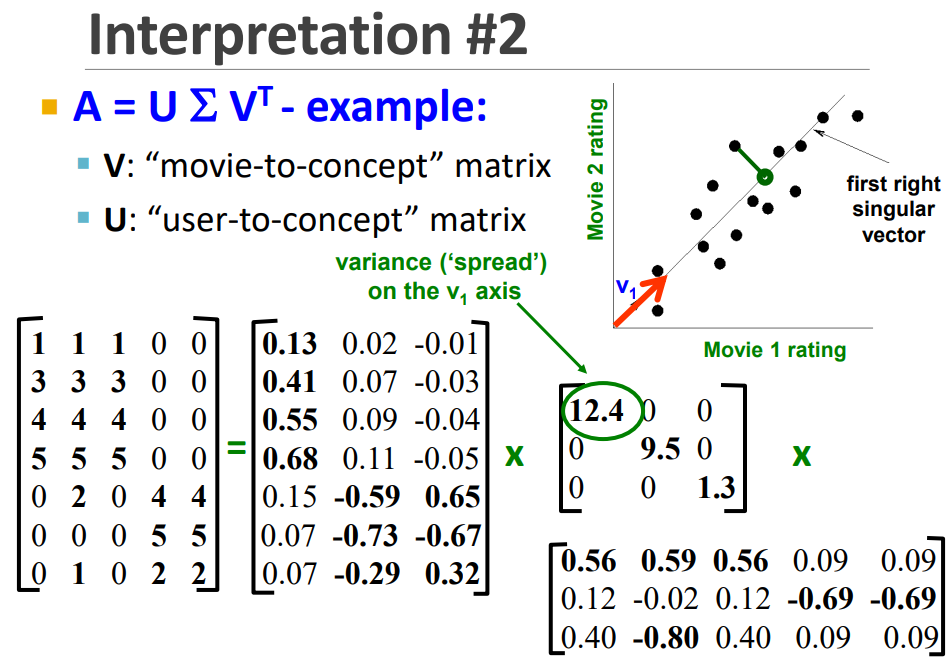
여기 SVD 예제에서는 결측값이 없다고 가정합시다. 행이 유저, 열이 영화입니다. R은 여기서 3입니다. 행렬의 12.4는 첫번째 열 concept이 얼마나 영향력 있는지를 의미합니다. 여기 첫번째 컨셉으로 Scifi-concept이라고 한 것은 사람이 영화 Matrix, Alien, Serenity를 보고 사람이 정한 것이라고 볼 수 있습니다. 다시 말해 이러한 컨셉까지는 SVD 알고리즘의 결과물이 아니고 사람이 정해준 것이라고 볼 수 있으니 헷갈리지 맙시다.
Interpretation

또 다른 예를 들면 U는 Documents-to-concept 유사도 행렬, V는 Words-to-concept 유사도 행렬이라고 하면, concept는 sports, politics, culture 등이 될 수 있겠네요. 일반적으로 컨셉은 여러 단어들을 포함하기 때문에 클러스터링 하기 용이하다고 할 수 있습니다.
Dimensionality Reduction
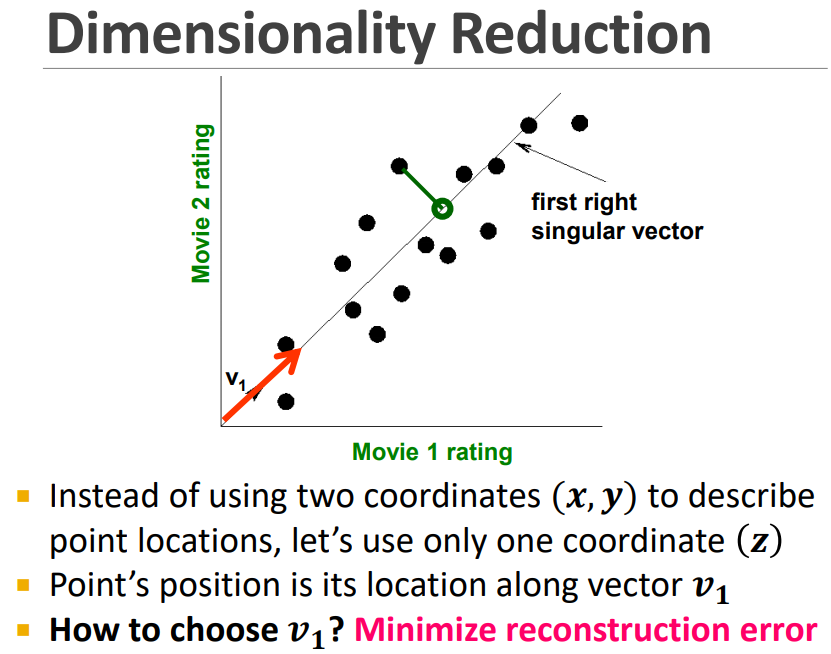
위 그래프를 가로지르는 v는 SVD의 결과물이라고 할 수 있습니다. 이 축과 같이, 어떻게 새로운 축을 찾을 수 있을까요?

Reconstruction Error를 최소화 하면 됩니다. 이를 통해 언제나 최적의 축을 얻을 수 있습니다.
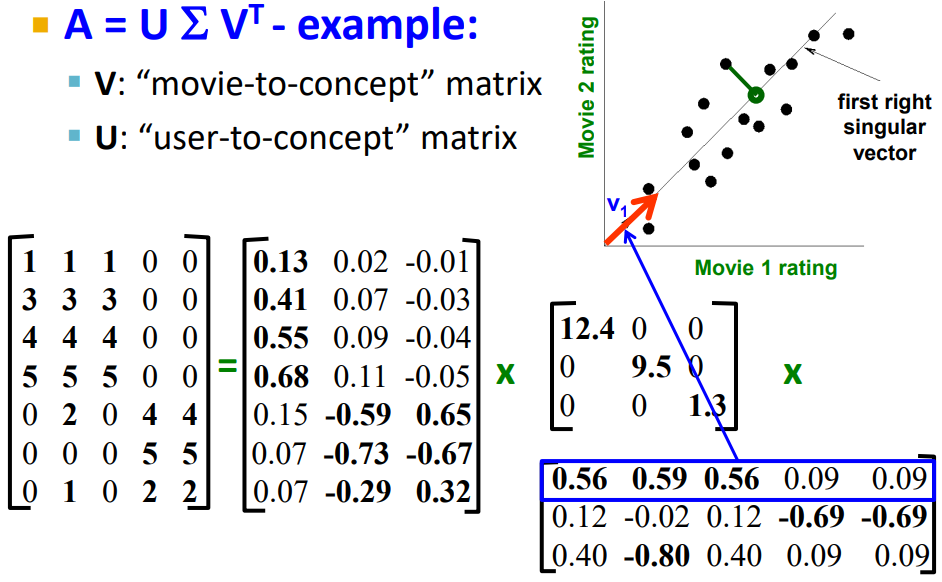
의 첫 번째 행은 축의 direction을 의미하고, 12.4는 새로운 축의 variance를 의미합니다. 마찬가지로 의 두 번째 행은 두 번째 축의 direction을 줍니다. 세 번째 행도 마찬가지입니다. 여기서도 동일하게 이 행들이 최적의 axis인 것을 수학적으로 보장할 수 있습니다.
Q. Variance가 작아야 좋은 것 아닌가요?
I am confused with that this value in means 'strength' in representing the concept. Isn't smaller variance in Sigma matrix better than larger variance value?
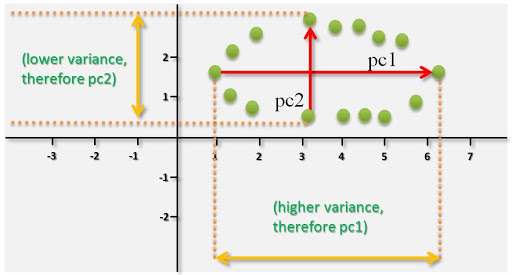
위와 같이 질문을 했는데, 데이터를 잘 표현하는 축은 분산을 크게 하는 것이 좋습니다. PCA 차원 축소 기법이 분산을 최대로 보존하는 축을 찾는 것과 같은 원리입니다. 아래 그림을 참고합니다. (이미지 출처)
Interpretation
1. Interpretation
2. Interpretation

3. Interpretation

작은 variance를 가진 랭크를 무시하면 best rank-k approximation of A. 아래 그림과 같이 됩니다.

Q. How many target dimentions should we keep?
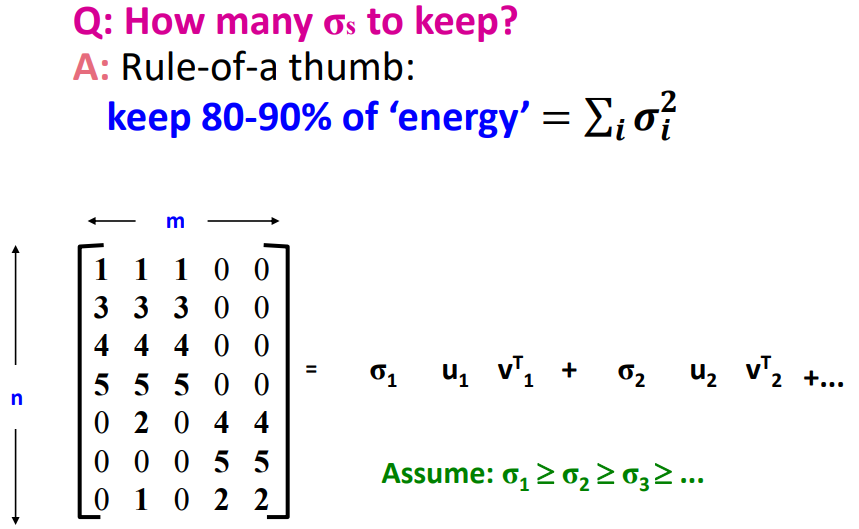
n차원에서 k차원으로 줄일 때, 이 k의 값을 어떻게 정할 수 있을까요? 기존 n차원에서의 의 합과 비교했을 때 80-90%의 수준을 유지하는 선에서 결정하면 됩니다.
