
GIF 출처 : https://www.amigoscode.com/courses/java
🖥 Contents
1 ) 함수형 프로그래밍 개념정리
1 ) 함수형 프로그래밍 개념정리
-
람다 대수 ( Lambda Calculus )
: 추상 함수를 이용하여 수학 연산을 표현하고 , 이를 변수에 바인딩 하는 방식- 구성 요소
① 추상화 ( Abstraction )
: 단일 입력을 받는 익명 함수 ( 람다 ) 를 의미한다.
② 응용 ( Application )
: 값에 추상화가 적용되어 결과를 생성하는데 이는 함수나 메소드 호출을 의미한다.
③ 베타 축약 ( β - reduction )
: 추상화된 변수를 적용된 인수로 대체한다.
- 구성 요소
-
표현식과 문장식 ( Expression & Statement )
① 표현식 ( Expression )
: 연산자 , 피연산자 , 메소드 호출로 구성되며 연산을 정의하고 결괏값을 계산한다.-> 제어 흐름이나 알고리즘을 설명하지 않고 , 연산의 논리를 선언적 문장으로 표현할 수 있어야 하는 선언적 프로그래밍 스타일은 함수형 프로그래밍 언어의 특징 중 하나이다.
② 문장 ( Statement )
: 동작을 기술한 독립적인 실행 단위를 의미하며 리턴값이 없는 메소드 호출을 포함한다. -
순수 함수 ( Pure Function )
: 순수 함수란 동일한 입력에 대해 항상 동일한 출력을 반환하며 어떠한 사이드 이펙트 없이 자기 충족적 성질을 가지는 함수를 의미한다.
public String getString(String str){
return str; //
}-
참조 투명성 ( Referentially Transparent )
: 참조 투명성이란 다른 프로그램을 작성할 때도 기존의 코드를 변경하지 않고 재사용할 수 있는 것을 의미한다.
-
불변성 ( Immutability )
: 초기화 된 이후 자료 구조를 변경할 수 없는 상태로 일관성을 보장하고 예측 가능하다. 불변성을 가지는 자료 구조를 직접 변경하는 대신 변경된 상태를 포함하는 업데이트된 새로운 버전을 생성해야 한다.
이때 , 구조 공유 ( Structure Sharing ) 을 사용하여 효율적인 복사 메커니즘을 통해 데이터 변경에 대한 비효율성을 최소화할 수 있다.
-
재귀 ( Recurssion )
: 동일한 형태의 문제를 부분적으로 해결하고 그 결과를 조합하여 최종적으로 원래의 문제를 해결하는 문제 기법으로 결과값을 반환할 때 까지 자기 자신을 반복적으로 호출한다.
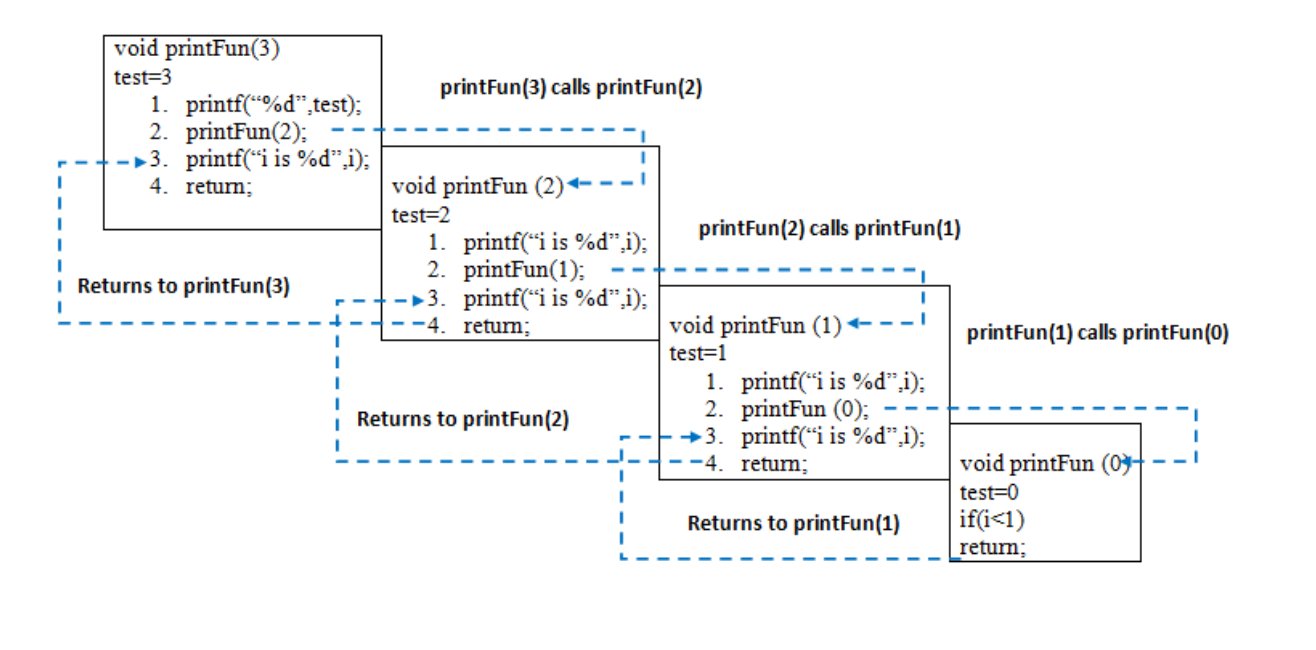
출처 : https://www.geeksforgeeks.org/introduction-to-recursion-2/
-
일급 함수 & 고차 함수 ( First - Class Function & Higher - Order Function )
① 일급 함수 ( First - Class Function )
: 함수 자체를 다른 함수에 인수로 전달하거나 반환값으로 사용할 수 있으며 변수에 할당할 수 있는 함수
② 고차 함수 ( Higher - Order Function )
: 일급 객체의 특성을 바탕으로 함수를 인수로 받거나 , 또는 함수를 결과로 반환하는 함수
-
커링 함수 ( Currying Function )
: 여러 개의 인수를 받는 함수들을 분리하여 인수를 하나씩만 받는 함수의 체인으로 변환하는 것
ex)
x = f(a,b,c)
h = g(a)
i = h(b)
x = i(c)
x = g(a)(b)(c) // 변환 // 자바의 람다 예시
Function<Interger,Function<Integer,Integer>> add = a -> (b->a+b));-
부분 적용 함수 애플리케이션 ( Partial Function Application )
: 기존 함수의 인수 중 일부만 제공하여 새로운 함수를 생성하는 과정으로 부분 적용된 함수에 대한 호출은 결과를 반환하며 커링 체인과 달리 또 다른 함수를 반환하지 않는다.
ex )
BiFunction<Integer,Integer> add = (a,b)-> (a+b);
Function<Integer,Integer> addT = b -> add.apply(10,b);
// add 함수를 사용한 부분 적용 함수- 느긋한 계산법 ( Lazy Evaluation )
: 표현식의 계산을 그 결과가 실제로 필요한 시점까지 지연시키는 전략으로 표현식을 어떻게 생성하는지와 해당 표현식을 언제 사용하는지에 대한 문제를 분리하는 개념이다.
예를 들어 자바의 함수형 프로그래밍에서는 람다 ( Lambda ) 를 들 수 있다. 람다식의 경우 식을 표현할 때에는 실행되지 않으나 해당 식을 다른 함수 혹은 라인에서 실행하게 될 경우에 해당 식의 실행이 결정된다.
ex )
Function<Integer,String> woojuiceFunc = number->user.getUsername(number); // 아직 실행 x
String username = woojuiceFunc.apply(1); // 람다식 실행 시점 -
메모이제이션 ( Memoization )
: 메모이제이션이란 함수의 호출결과 값을 함수에 저장해놓고 , 같은 입력이 반복될 때 저장한 값을 반환하는 것을 의미한다.메모이제이션의 경우 동일한 인수를 사용하여 이루어진 후속 호출을 모두 이전에 계산된 결과로 대체할 수 있기 때문에 메모리 최적화 방식에서 사용된다.
-
아리티 ( Arity )
: 함수의 인수 개수를 의미하며 함수가 받아들이는 피연산자의 수를 말한다.
