Likelihood Function without Deep Learning
- 입력으로 주어진 확률 분포(파라미터)가 데이터를 얼마나 잘 설명하는지 나타내는 점수(Likelihood)를 출력하는 함수
• 입력: 확률 분포를 표현하는 파라미터
• 출력: 데이터를 설명하는 정도 - 데이터를 잘 설명하는 확률분포의 "파라미터"를 알 수 있는 방법
• 데이터가 해당 확률 분포에서 높은 확률 값을 가질 것 - Likelihood는 확률값의 곱으로 표현됨 (underflow의 가능성)
• 따라서 Log를 취하여 곱셈을 덧셈으로 바꾸고, Log Likelihood로 문제를 해결
• 덧셈이 곱셈보다 연산도 빠름
MLE via Gradient Ascent
- 랜덤 생성 대신, Gradient Ascent를 통해, likelihood 값을 최대로 만드는 파라미터(𝜃)를 찾자.
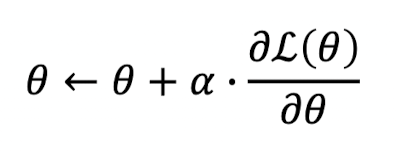
- 하지만 대부분의 딥러닝 프레임워크들은 Gradient Descent만 지원
• 따라서 maximization 문제에서 minimization 문제로 접근
(Gradient Descent를 통해 Negative Log Likelihood (NLL)을 최소화하는 𝜃 찾기!)
Frontend & Artificial Intelligence