딥러닝 학습방법 이해

신경망을 수식으로 분해해보자

신경망은 선형모델과 활성함수(activation function)를 합성한 함수 (선형 -> 비선형)
• 활성함수를 쓰지 않으면 딥러닝은 선형모형과 차이가 없음
• 시그모이드(sigmoid) 함수나 tanh함수는 전통적으로 많이 쓰이던 활성함수지만 딥러닝에선 ReLU함수를 많이 쓰고 있다

sigmoid vs Tanh

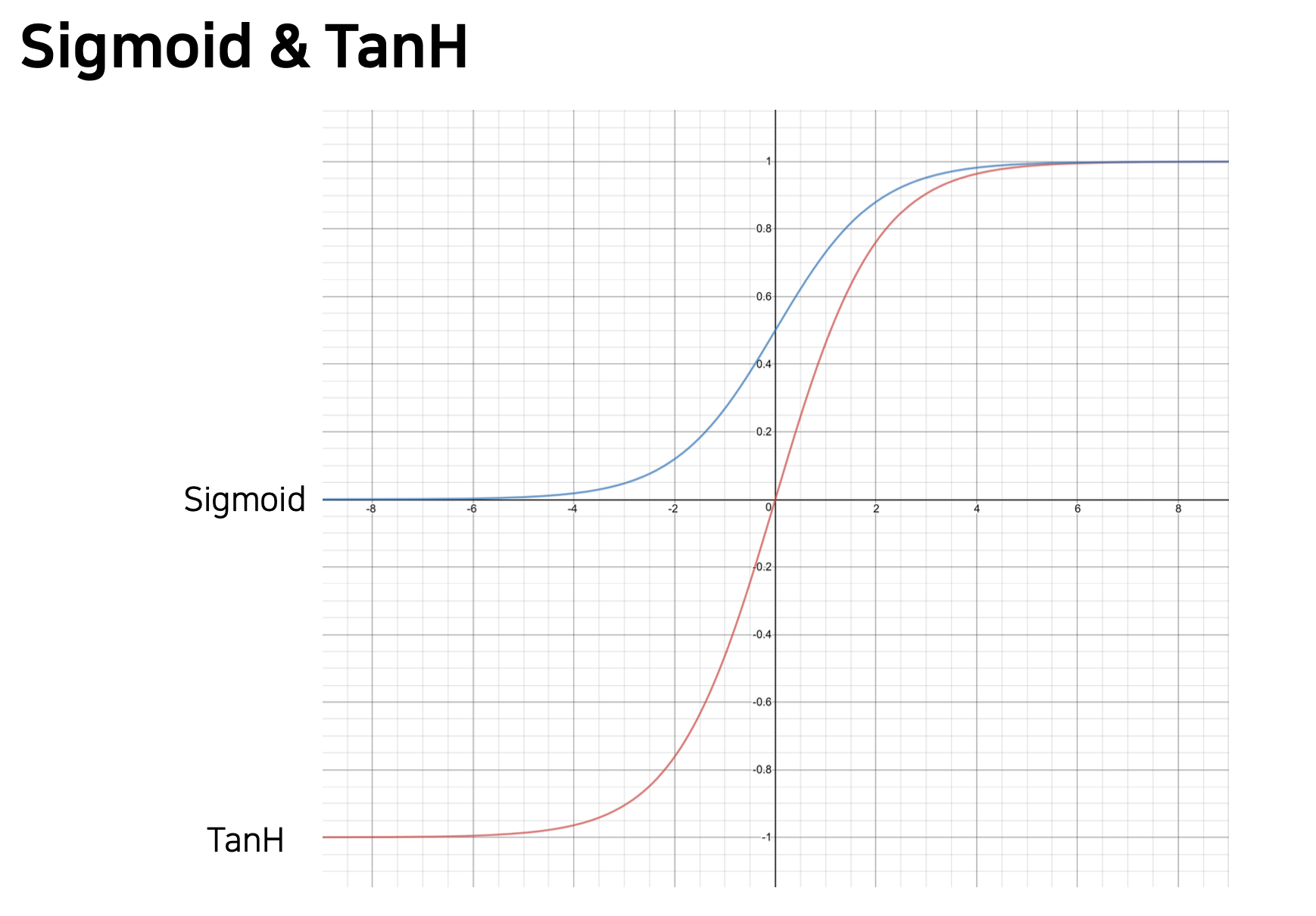
sigmoid 범위 : 0 ~ 1
TanH 범위 : -1 ~ 1

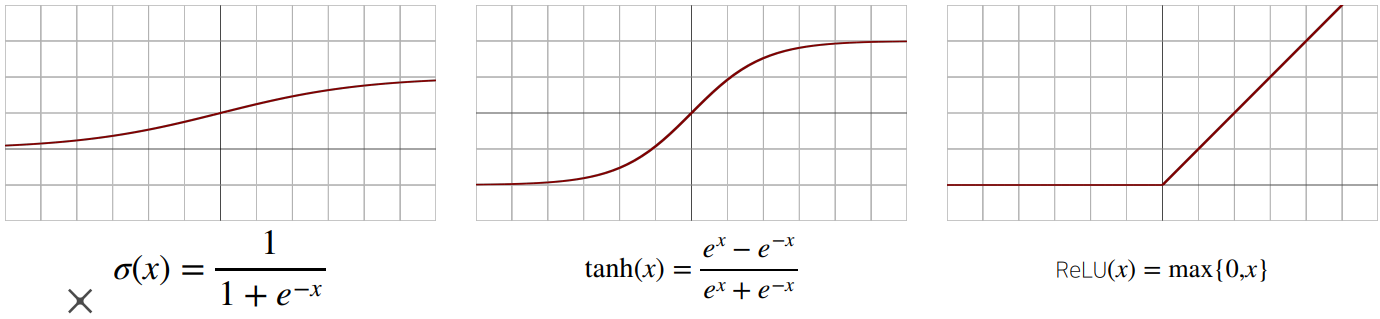
다층(multi-layer)퍼셉트론(MLP)은 신경망이 여러 층 합성된 함수

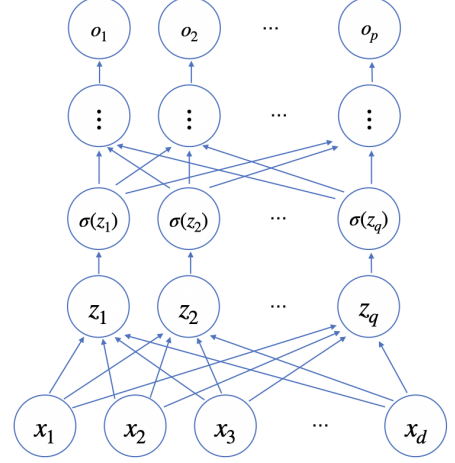
순차적인 신경망 계산을 순전파(forwardpropagation)라 부른다

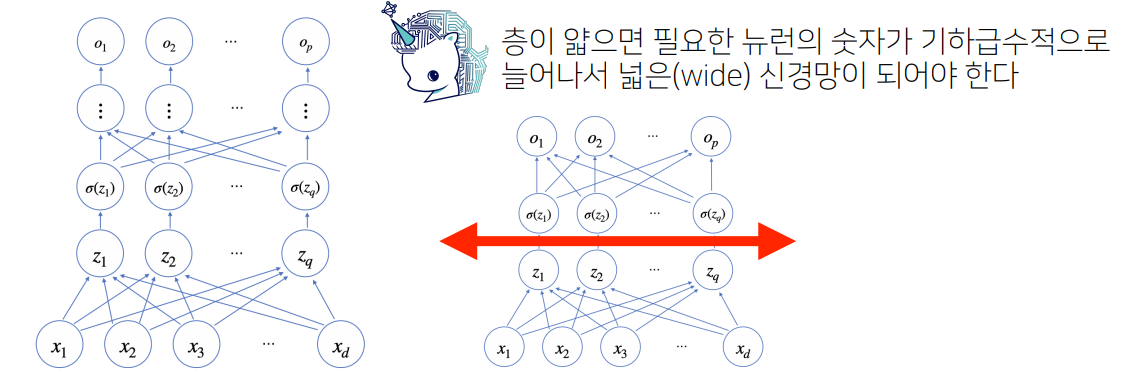
왜 층을 여러개 쌓는가?

층이 깊을수록 목적함수를 근사하는 데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능
layer가 깊다, 너비가 넓다 -> 파라미터($w, b$)수가 많다

역전파 알고리즘

딥러닝은 역전파(backpropagation)알고리즘을 이용하여 각 층에 사용된 패러미터를 학습
각 층 패러미터의 그레디언트 벡터는 윗 층부터 역순으로 계산

• 매번 처음부터 새로 계산할 필요 없이 필요한 부분을 재활용(chain rule을 통해) 하기 때문에, 반복되는 미분과정을 효율적으로 만들 수 있다

loss를 각 레이어의 파라미터마다 그냥 미분하는 것은 매우 비효율적

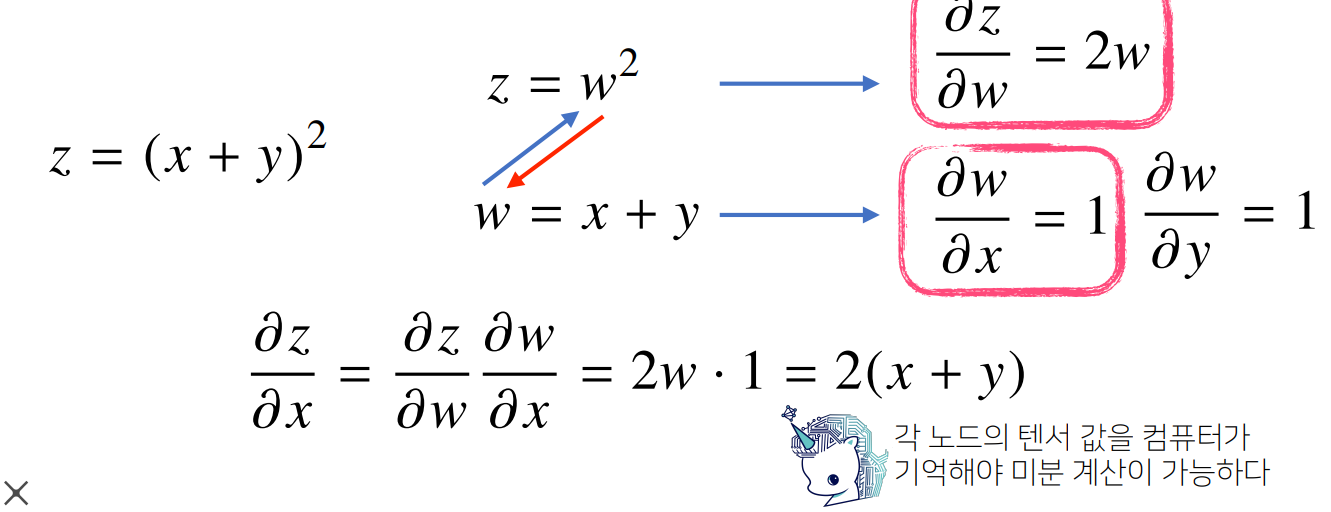
Gradient Vanishing (기울기 소실)

• 깊은 네트워크를 구성하게 되면 점점 gradient가 작아지는 현상
• 따라서 깊은 신경망을 학습하기 어렵게 됨
  - Chain rule로 펼쳤을 때 sigmoid & tanH 함수에 대한 미분 값은 항상 1보다 같거나 작다
  • DNN이 깊다 = 활성함수의 사용 횟수가 증가한다
    - 따라서 입력에 가까운 레이어는 파라미터에 대해 미분했을 때 1보다 작은 값이 반복적으로 곱해질 것이기 때문에 최소 loss를 찾기 위해 업데이트 되는 크기가 매우 작아지게 될 것

ReLu (Rectified Linear unit)

• ReLU를 통해 gradient vanishing 문제를 어느 정도 해결 할 수 있다.
• 두개의 linear 함수로 이루어져 있음
• 양수 부분의 기울기는 항상 1이므로 학습 속도가 빠르다. (최적화가 더 쉽다)
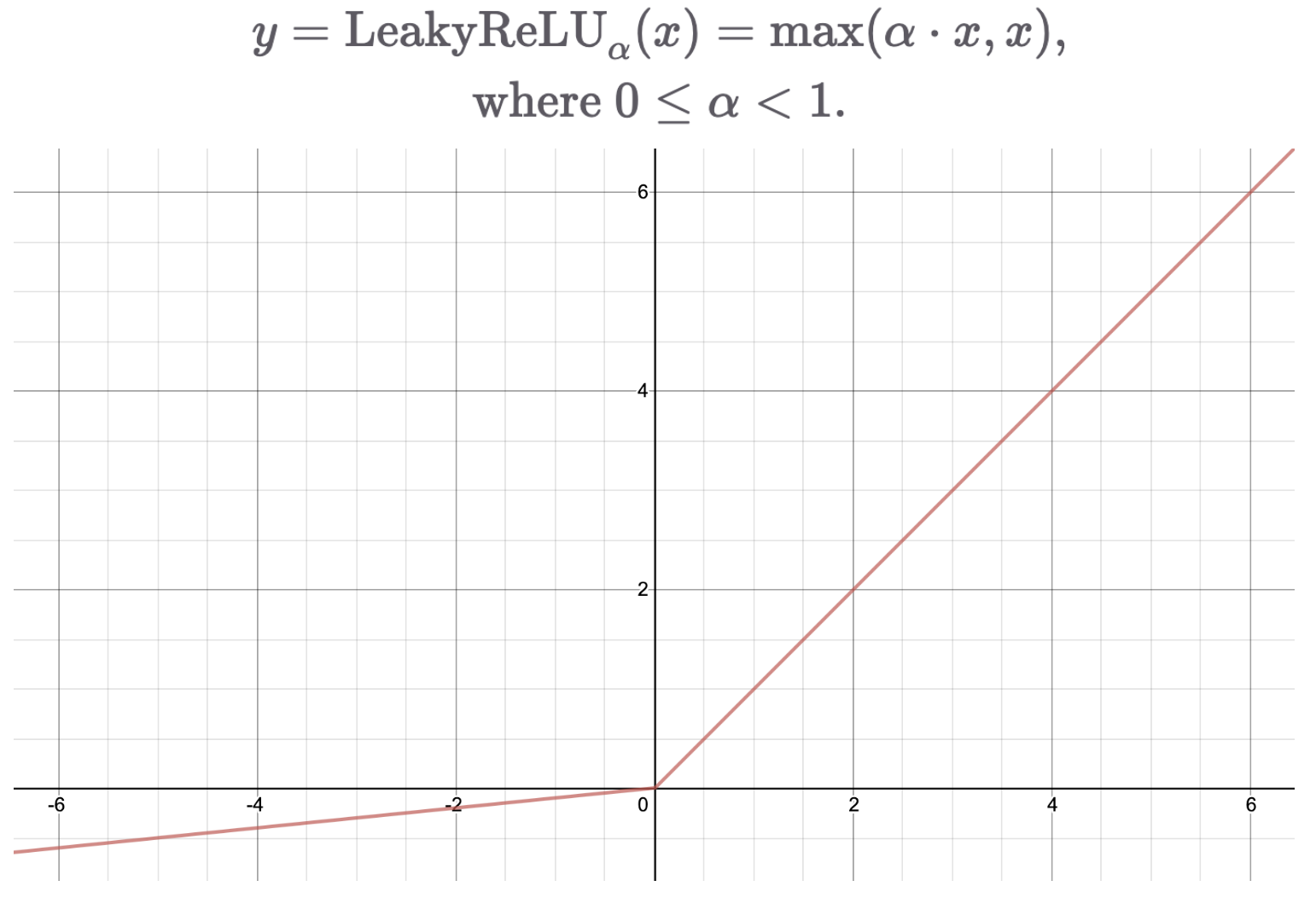
• ReLU의 입력 값이 음수인 경우, 이전 레이어는 학습이 불가하지만 Leaky ReLU를 통해 단점을 극복할 수 있다. (기울기 조절 가능)

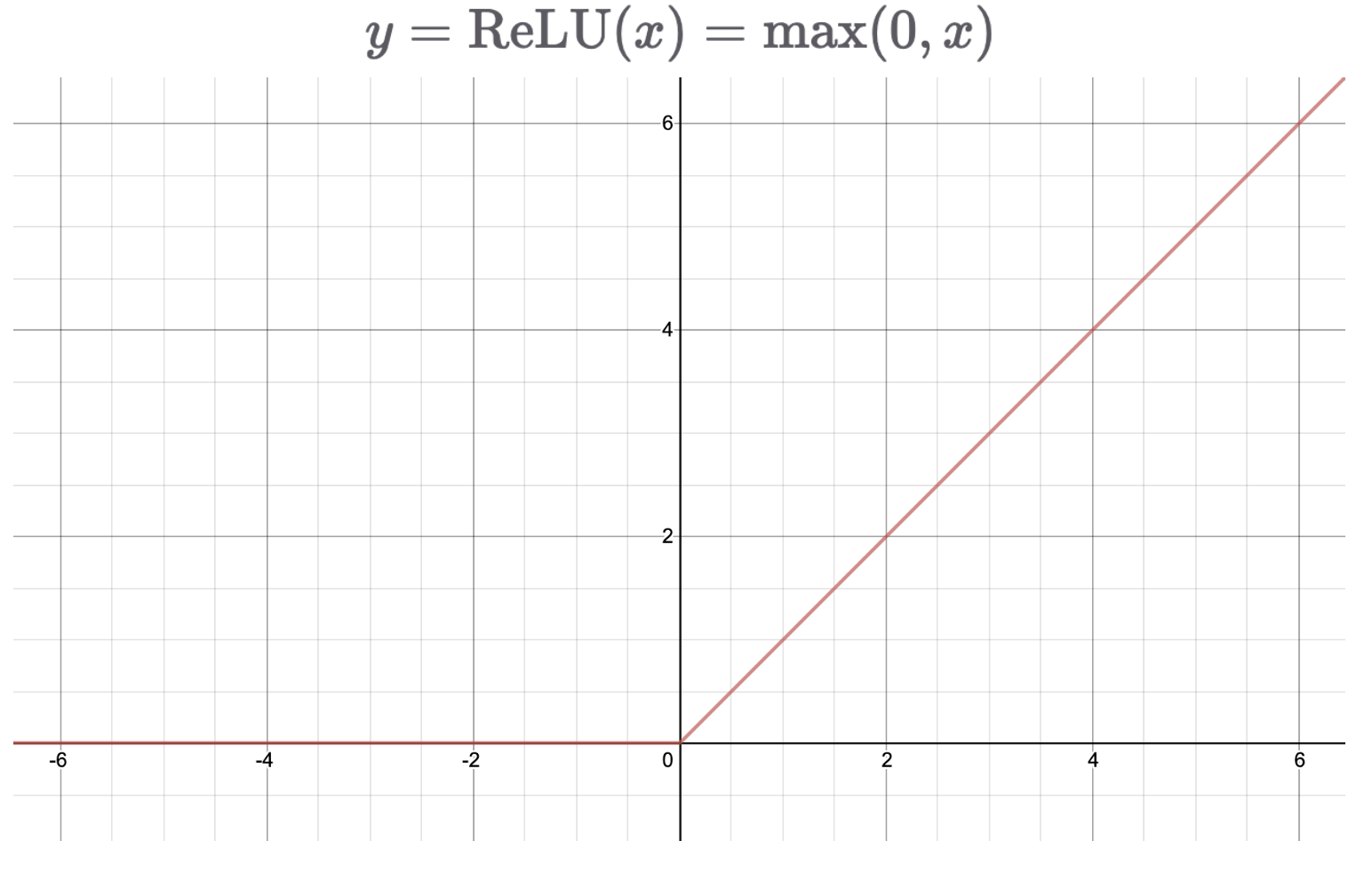
소프트맥스

소프트맥스(softmax)함수는 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산
분류 문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측