[자료구조] 순차 탐색 알고리즘과 시간 복잡도 분석

다음은 순차 탐색 알고리즘을 구현한 LSearch 함수 코드다.

#include <stdio.h>

int LSearch(int ar[], int len, int target)
{
  int i;
  for(i=0; i<len; i++)
  {
    if(ar[i] == target)
      return i;         // 찾은 대상의 인덱스 값 반환
  }
  return -1;            // 찾지 못했음을 의미하는 값 -1 반환
}

int main(void)
{
  int arr[] = {3,5,2,4,9};
  int idx;
  
  idx = LSearch(arr, sizeof(arr)/sizeof(int), 4);
  if(idx == -1)
    printf("탐색 실패 \n");
  else
    printf("타겟 저장 인덱스: %d \n", idx);
  
  idx = LSearch(arr, sizeof(arr)/sizeof(int), 7);
  if(idx == -1)
    printf("탐색 실패 \n");
  else
    printf("타겟 저장 인덱스: %d \n", idx);
  
  return 0;
}

👉 이제 위 코드의 시간 복잡도를 분석해서 연산횟수 함수 T(n)을 구해보자.

이 알고리즘의 핵심이 되는 연산자는 if(ar[i] == target) 에 등장하는 '==' 연산자다. 이 동등비교 연산자에 따라 <연산이나 ++연산의 횟수가 결정된다. 이처럼, 알고리즘의 핵심 연산이 무엇인지 잘 판단하여 시간 복잡도를 계산해야 한다.

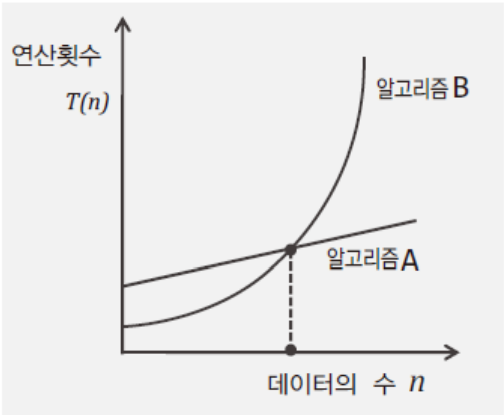
위 그림에서 확인할 수 있듯, 데이터의 수가 많아지면 worst case에 수행하게 되는 연산의 횟수는 알고리즘 별로 차이가 크다. 따라서 알고리즘의 성능을 판단하는 데 중요하게 볼 것은 worst case인 것이다.