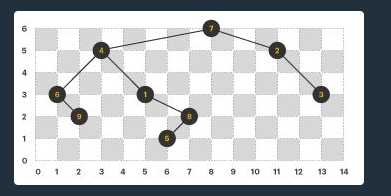
문제
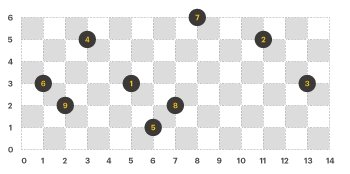
프로그래머스의 길 찾기 게임 문제는 트리 구조와 좌표 기반 정렬을 이용하여 이진 트리를 구성하고, 전위 순회와 후위 순회를 통해 답을 구하는 문제입니다.
이 문제는 트리를 구성하고 순회하는 방법에 대한 이해가 필요합니다.
문제 설명
주어진 입력은 노드들의 좌표가 포함된 배열입니다. 배열의 각 원소는 [x, y]로 노드의 위치를 나타내며, y는 트리의 깊이를 의미하고 x는 트리에서의 위치를 의미합니다.
노드를 좌표 기준으로 정렬하여 이진 트리를 구성합니다.
- y값이 큰 노드가 루트에 가깝고, x값이 작을수록 왼쪽에 위치합니다.
- 전위 순회와 후위 순회의 결과를 출력해야 합니다.
문제 풀이 접근
- 노드 정렬:
- 노드들을 y값을 기준으로 내림차순 정렬합니다. => 이를 통해 root 노드를 알 수 있고, 같은 레벨에 위치한 노드들을 체크할 수 있습니다.
- y값이 동일하다면 x값을 기준으로 오름차순 정렬하여 같은 레벨에서는 왼쪽 노드가 오른쪽 노드보다 앞에 오도록 합니다.
- 이진 트리 구성:
- 정렬된 순서에 따라 첫 번째 노드를 루트로 삼고, 이후의 노드들을 트리에 추가합니다.
- 노드 삽입 규칙:
- 루트보다 x값이 작으면 왼쪽 서브트리에 삽입합니다.
- 루트보다 x값이 크면 오른쪽 서브트리에 삽입합니다.
- 트리 순회:
- 전위 순회(루트-왼쪽-오른쪽)와 후위 순회(왼쪽-오른쪽-루트)를 통해 순회 결과를 얻습니다.
코드 구현
import java.util.*;
class Solution {
private List<Integer> preorderList;
private List<Integer> postorderList;
class TreeNode {
int x, y, index;
TreeNode left, right;
TreeNode(int x, int y, int index) {
this.x = x;
this.y = y;
this.index = index;
}
}
public int[][] solution(int[][] nodeinfo) {
List<TreeNode> nodes = new ArrayList<>();
// 노드들을 TreeNode 객체로 만들고, 정렬을 위해 리스트에 추가
for (int i = 0; i < nodeinfo.length; i++) {
int x = nodeinfo[i][0];
int y = nodeinfo[i][1];
nodes.add(new TreeNode(x, y, i + 1)); // index는 1-based
}
// y 기준 내림차순, x 기준 오름차순으로 정렬
nodes.sort((a, b) -> {
if (a.y == b.y) {
return Integer.compare(a.x, b.x);
} else {
return Integer.compare(b.y, a.y);
}
});
// 트리 구성
TreeNode root = nodes.get(0);
for (int i = 1; i < nodes.size(); i++) {
insertNode(root, nodes.get(i));
}
preorderList = new ArrayList<>();
postorderList = new ArrayList<>();
// 전위 순회
preorderTraversal(root);
// 후위 순회
postorderTraversal(root);
// 결과 배열로 변환
int[][] answer = new int[2][nodeinfo.length];
for (int i = 0; i < preorderList.size(); i++) {
answer[0][i] = preorderList.get(i);
}
for (int i = 0; i < postorderList.size(); i++) {
answer[1][i] = postorderList.get(i);
}
return answer;
}
private void insertNode(TreeNode parent, TreeNode child) {
if (child.x < parent.x) {
if (parent.left == null) {
parent.left = child;
} else {
// 부모노드보다 값이 작은데 subTree의 좌측이 null 이 아니라면 한 level을 더 내려가서 탐색해야한다.
insertNode(parent.left, child);
}
} else {
if (parent.right == null) {
parent.right = child;
} else {
// 부모노드보다 값이 큰데 subTree의 우측이 null 이 아니라면 한 level을 더 내려가서 탐색해야한다.
insertNode(parent.right, child);
}
}
}
private void preorderTraversal(TreeNode node) { // 전위 순회
if (node != null) {
preorderList.add(node.index); // 루트 처리
preorderTraversal(node.left); // 왼쪽 서브트리
preorderTraversal(node.right); // 오른쪽 서브트리
}
}
private void postorderTraversal(TreeNode node) { // 후위 순회
if (node != null) {
postorderTraversal(node.left); // 왼쪽 서브트리
postorderTraversal(node.right); // 오른쪽 서브트리
postorderList.add(node.index); // 루트 처리
}
}
}코드 설명
- TreeNode 클래스:
- TreeNode는 트리 노드를 나타내는 클래스입니다. 각 노드는 x, y 좌표와 index (노드 번호)를 가집니다.
- 노드 정렬:
- 입력 배열을 TreeNode 객체로 변환하고, y 기준 내림차순, x 기준 오름차순으로 정렬합니다. y가 곧 level을 뜻하고 x가 곧 값을 뜻하기 때문입니다.
- 트리 구성:
- 첫 번째 노드를 루트로 설정하고, 나머지 노드들을 루트 노드부터 삽입합니다.
- insertNode 메서드는 트리를 구성하는 재귀 함수로, 각 노드를 적절한 위치에 삽입합니다.
- 전위 및 후위 순회:
- preorderTraversal 함수는 전위 순회를 수행하며, preorderList에 순회 결과를 저장합니다.
- postorderTraversal 함수는 후위 순회를 수행하며, postorderList에 순회 결과를 저장합니다.
- 결과 반환:
- preorderList와 postorderList를 결과 배열에 넣어 반환합니다.
추가적인 개념
순회에 대한 기본적인 개념을 다시 한 번 복습하기
순회
이진 트리에서 노드를 방문하는 순서를 정의하는 트리 순회(traversal) 방법입니다. 각 순회 방식은 노드의 루트(root)와 자식 노드(left, right)를 방문하는 순서에 따라 구분됩니다.
전위 순회(Preorder Traversal), 중위 순회(Inorder Traversal), 후위 순회(Postorder Traversal) 모두 깊이 우선 탐색(Depth-First Search, DFS)의 일종입니다.
DFS는 트리나 그래프에서 한 경로를 끝까지 탐색한 후, 다른 경로로 이동하는 방식의 탐색 방법입니다. 트리의 순회 방식은 DFS의 한 형태로 볼 수 있으며, 그 이유는 트리를 한쪽 방향으로 깊이 들어가며 순회하기 때문입니다.
다음과 같은 그래프가 있다고 가정해보겠습니다.

전위 순회
전위 순회에서는 루트 노드를 먼저 방문하고, 그 다음에 왼쪽 자식 노드를 방문한 후 오른쪽 자식 노드를 방문합니다.
[방문순서]
루트 → 왼쪽 → 오른쪽
전위 순회 결과: A → B → D → E → C → F
중위 순회
중위 순회에서는 왼쪽 자식 노드를 먼저 방문하고, 그 다음에 루트 노드를 방문한 후 오른쪽 자식 노드를 방문합니다. 중위 순회는 이진 탐색 트리에서 노드를 오름차순으로 방문하는 순서로도 자주 사용됩니다.
[방문순서]
왼쪽 → 루트 → 오른쪽
중위 순회 결과: D → B → E → A → C → F
후위 순회
후위 순회에서는 왼쪽 자식 노드를 먼저 방문하고, 그 다음에 오른쪽 자식 노드를 방문한 후 루트 노드를 방문합니다. 후위 순회는 트리의 노드를 삭제할 때, 혹은 자식 노드를 모두 처리한 후 부모 노드를 처리해야 하는 경우에 사용됩니다.
왼쪽 → 오른쪽 → 루트
후위 순회 결과: D → E → B → F → C → A