Real-Time System (4) : L&L Bound

서론

이 포스트에서는 모든 task의 period, execution time을 알지 못하는 상황에서도 수행 가능한 schedulability test인 utilitzation bound test를 소개한다.

Utilization Bound 검사의 필요성

앞선 포스트에서 소개한 RTA, TDA는 exact analysis라고도 한다. 이는 모든 task의 period와 execution time을 알 때 정확한 최대 resposne time을 구하여 주어진 deadline보다 작은지를 검사한다. 하지만, exact analysis는 아래의 단점이 있다.

• 복잡도가 커서 상대적으로 오래 걸린다.
• e (execution time), p (period)를 알아야 하는데, design phase에는 이를 모두 알기 어렵다.

따라서 e, p를 모르더라도 design phase에서도 schedulability를 알 수 있는 방법이 필요하다. 그 중 가장 보편적으로 사용하는 것이 utilization bound를 검사하는 방법이다.

Utilization bound의 개념

기본적으로 utilization은 task model을 설명할 때 간단하게 식만 짚고 넘어간 적이 있으나, periodic task들의 집합에서는 아래 식과 같다.

$U = \sum_{i}\frac{e_i}{p_i}$

직관적으로 $\frac{e_i}{p_i}$는 전체 CPU 시간 중 얼마의 비율을 task $\tau_i$를 수행하는데 사용할 것이냐에 대한 지표다. 따라서 모든 task에 대해 이 값을 더하면, 전체 task set를 실행했을 때 평균적으로 CPU들이 task를 실행하는 시간의 비율이 계산된다.
그렇지 않을 것 같다면 실제로 hyperperiod (모든 period의 최소공배수)만큼에 대해 각 task가 실행되는 시간들을 다 더해보면 정말 그렇다는 것을 확인할 수 있다.
ex)
Task 1: $e_1 = 3, p_1 = 10$
Task 2 : $e_2 = 2, p_2 = 5$
Task 3 : $e_3 = 7, p_3 = 20$
이면 utilization $U = 0.3 + 0.4 + 0.35 = 1.05$이고,
hyperperiod $HP = 20$ 에 대해 Task 1은 2번, Task 2는 4번 실행되므로 총 실행시간은 3x2+2x4+7= 21이다. 계산해보면 딱 $U$만큼의 비율이다.
그런데 U가 1을 넘는 것을 확인할 수 있다. 직관적으로 생각했을 때 utilization이 1.05이라는 것은, 1이라는 시간 동안 CPU가 1.05만큼의 workload를 수행해야하는데 이는 물리적으로 불가능하다. 즉, utilization이 1보다 크면 schedulable하지 않다는 것이 자명하다.
당연해보이는 이 개념이 가장 쉽게 utilization bound를 적용한 것이다.

Utilization bound의 기본
어떤 스케줄링 알고리즘을 사용하더라도 utilization이 1보다 크면 schedulable하지 않다.

여담으로 다음 포스트에서 설명하겠지만 EDF 알고리즘을 사용하는 경우에는 utilization이 1 이하이면 모두 schedulable하다.
그런데 위 정리와 EDF에 대한 말에서 중요한 차이점이 있다. EDF같은 경우에는 task set의 utilization이 1 이하이면 schedulable하다는 것을 알 수 있으나, 다른 알고리즘 (RM)과 같은 경우에는 task set의 utilization이 0.8일 때 schedulable한지 아닌지 알 수가 없다. 즉, schedulable하다는 것을 보장할 수 있는 최대의 utillization bound 값을 알 필요가 있다. 다시 말하자면 일반적으로 utilization bound를 구한다는 것은 아래 식의 $U_{bound}$ 값을 구하는 것이다.

$if\ U = \sum_{i}\frac{e_i}{p_i} \le U_{bound}, task \ is \ schedulable$

일반적으로 utilization bound 검사는 task set이 schedulable하기 위한 충분조건이다. 즉, utilization bound check를 만족했을 때 schedulable함은 보장되지만, 만족하지 않는다고 꼭 schedulable하지 않다는 의미는 아니다. exact analysis에 비해 가지는 단점이라고 볼 수 있다.

L&L Bound

RM에 대해서는 Liu와 Layland가 utilization bound를 증명했다. RM 자체가 static priority 분야에서 워낙 많이 쓰이다보니 이 식은 여러 논문에서 참조 논문으로 사용한다.

[L&L Bound]
RM에 대해 n개의 periodic task는 아래 조건인 경우 schedulable하다.
$\frac{e_1}{p_1} + \frac{e_2}{p_2} + \dots + \frac{e_n}{p_n} \le n(2^{1/n} - 1)$
U(1) = 1.0이며, n이 커지면 bound는 $ln 2 \sim 0.69$로 수렴한다.

harmonic한 task set (각 period가 자신보다 짧은 period에 대해 정수배)인 경우에는 모든 n에 대해 bound가 1이라고 한다.

이 bound를 알기 위해서는 barely schedulable한 task set을 구할 수 있어야 한다.
barely schedulable이라는 말을 바로 이해하기는 어렵지만, 직역하자면 겨우 스케줄 가능한 task set을 찾는 것이다. 직관적으로 $U_{bound}$가 커야 더 많은 task set을 schedulable하다고 판단할 수 있으므로, schedulable하면서도 utilization이 큰 task set을 찾는 것이 중요하다. 따라서 fully utilized된 task set들만을 search space로 살펴볼 것이다. 이 때 fully utilized란 주어진 알고리즘 하에서 deadline miss는 없되, CPU가 idle한 시간 없이 계속 실행되는 task set을 말한다. utilization이 1이라는 것과는 다른 의미임에 유의하자. utilization이 1이면 자명하게 fully utilized이겠지만, 사실 task set 내의 각 (e, p) 조합에 따라 fully utilized될 수 있는 task set은 상당히 많다. 이는 뒤의 증명에서의 예시를 보면 더 쉽게 이해할 수 있다. 어쨌든 deadline miss가 없는 task set이므로 schedulable함은 보장된다.

이제 fully utilized set 중 가장 utilization이 작은 task set의 조합을 찾는다면,
하지만 적어도 해당 utilization보다 작은 utilization을 갖는 task set들은 schedulable하다고 볼 수 있다.

Barely Schedulable Task Set

이 소문단에서는 barely schedulable한, 즉 fully utilized이면서 가장 utilization이 작게 되는 task set의 성질에 대해 알아볼 것이다. 결국 이 task set의 utilization을 $U_{bound}$로 사용할 것이기 때문에 증명의 과정이라고도 볼 수 있다.

1. No-overflow

위 그림을 보자. 두 task set 모두 CPU가 계속 실행되므로 fully utillized라고 생각할 수 있다. Task 1에 대해 9까지 실행되지 않은 게 아니냐고 할 수 있지만, 적어도 실행될 수 있는 한에서는 다 실행되긴 했으니, fully utilized라고 생각하자. (이 정의에 대해서는 확실하진 않다.)
두 task set에서 다른 것은, 왼쪽 task set은 task 2의 period가 끝난 이후에도 task 1이 실행된다는 것이다. 이를 overflow가 있다고 하는데, 두 task의 execution time을 조정하여 오른쪽처럼 overflow가 없도록 task set을 만들 수 있다. 위 그림에서 보라색으로 색칠된 부분의 길이를 각각 $\Delta$라고 하자. 이 때 각 task set의 utilization을 비교하면,

• 왼쪽 : $U_1 = 2/3 + 2/7$
• 오른쪽 : $U_2 = (2-\Delta)/3 + (2+2\Delta)/7$

$U_2 - U_1 = -\Delta/3 + 2\Delta/7 < 0$이므로 $U_2$가 더 작은 것을 확인할 수 있다. 즉, overflow가 없는 task set의 utilization이 더 작다.

일반적인 경우에 대해서는, overflow가 일어나는 task의 period $p_1$이 $p_2$보다 더 작을 것이기 때문에 $e_1$이 $\Delta$만큼 줄어든다면, $e_2$는 $\lfloor \frac{p_2}{p_1} \rfloor$ 만큼 늘어난다. 그렇게 되면 utilization의 변화는
$U_2 - U_1 = -\Delta/p_1 + \Delta \times \lfloor \frac{p_2}{p_1} \rfloor / p_2 < -\Delta/p_1 + \Delta \times \frac{p_2}{p_1} / p_2 = 0$
이므로 결국 utilization이 줄어든다. 따라서 일반적으로 overflow가 없을 때 utilization이 더 작다.

2. 각 task pair의 period 비율이 2보다 작아야 한다.

1번 성질은 execution time의 성질에 대해 알아봤다면 2번은 period에 대한 것이다. 위 그림에서 두 task set은 모두 fully utilized이다. 이 때 주기가 짧은 $p_1$의 주기를 좀 더 길게 하여 왼쪽의 task set을 오른쪽의 task set처럼 만들 수 있다. 두 task set의 utilization을 비교하면,

• 왼쪽 : $U_1 = 1/3 + 4/7$
• 오른쪽 : $U_2 = 1/6 + 5/7$

오른쪽에서 utilization이 늘어난 양은 1/7인데, 줄어든 양은 1/6이므로 utilization이 감소했음을 알 수 있다. 즉, period의 비율 차이가 없을수록 utilization이 작다. RM을 사용하므로 period가 짧은 쪽이 더 높은 priroity를 가지는데, 한 쪽의 period가 짧다는 것은 두 period의 비율이 1보다는 당연히 크다는 것이므로, 직관적으로는 2보다만 작게 만들면 최소의 utilization을 만들 수 있을 것이다.

일반적으로 두 period의 비율이 k인 경우에는 ($\lceil \frac{p_2}{p_1} \rceil = k$), $k > \frac{p_2}{p_1} > k-1$이므로 $p_1$를 $k-1$배 한다면, 두 period의 비율이 $\frac{k}{k-1} > \frac{p_2}{(k-1)p_1} > 1$이므로 $\lceil \frac{p_2}{(k-1)p_1} \rceil = 2$로 2배 이하가 된다. 이 경우 period를 늘리기 전후의 utilization을 비교하면

• $p_1$일 때 : $\frac{e_1}{p_1} + \frac{e_2}{p_2}$
• $(k-1)p_1$일 때 : $\frac{e_1}{(k-1)p_1} + \frac{e_2+(k-2)e_1}{p_2}$

$(\frac{e_1}{p_1} + \frac{e_2}{p_2}) - (\frac{e_1}{(k-1)p_1} + \frac{e_2+(k-2)e_1}{p_2}) = (\frac{(k-2)e_1}{(k-1)p_1} + \frac{(k-2)e_1}{p_2}) > 0 \ (\because (k-1)p_1 < p_2)$

이므로 period를 늘리는 편이 일반적으로도 utilization이 감소함을 알 수 있다.

Calculating L&L Bound

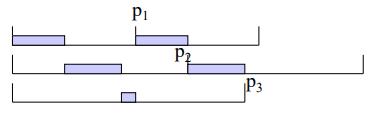
이제 우리는 barely schedulable task set의 성질을 알았다. 이를 통해 각 task들의 execution time을 구할 수 있는데, 위 그림에서도 확인할 수 있듯이 overflow가 없고, 두 task의 period의 비율이 2 이하이려면, 각 task의 execution time이 다음 priority task의 period에서 자신의 period를 뺀 만큼이어야 한다. 즉,

이다.
또 fully utilized task를 가정했기 때문에 가장 priority가 낮은 task는 나머지 task들이 2번씩 실행되고 남은 양이다. (그림에서 $e_3$를 생각하면 이해가 빠르다.) 즉,

이다.

이제 우리는 utilization $U = \frac{e_1}{p_1} + \dots + \frac{e_n}{p_n}$이 최소가 되는 조건을 확인하면 된다. $r_i = \frac{p_{i+1}}{p_i}$로 놓으면, utilization 식은

처럼 나타낼 수 있다. 최소의 U라는 것은 각 $r_i$에 대해 $\frac{\delta U}{\delta r_i} = 0$이라는 것이므로 미분방정식을 통해 식을 풀 수 있다.

$r_1$에 대해서 식을 풀어보면 $1 - \frac{2}{r_1^2 r_2 \dots r_{n-1}} = 0$이므로, $r_1^2 r_2 \dots r_{n-1} = 2$이다.
마찬가지로 $r_2$에 대해서 식을 풀어보면 $r_1 r_2^2 \dots r_{n-1} = 2$이다.
두 식을 나누면 $r_1 = r_2$이다.
나머지 $r_i$에 대해 이를 반복하면, 최종적으로는 모든 $r_i$가 같다는 것을 알 수 있다.
따라서 $r_1^2 r_2 \dots r_{n-1} = 2$에 대입하면 모든 $r_i = 2^{1/n}$이다.
utilization 식에 이 값을 대입하면 최종적으로 utilization은 L&L Bound인 $n(2^{1/n} - 1)$가 계산됨을 알 수 있다.

Harmonic Task Set에 대한 L&L Bound

harmonic task set 관련해서 증명이 찾아도 나오지 않았다. 그리고 원래 알던 harmonic task set의 정의와 논문에서의 정의가 좀 달라서 맞는걸 찾는데 좀 오래걸렸다. 논문에서는 가장 긴 period가 다른 period의 정수배이기만 하면 된다고 명시되어있다.

[Harmonic Task Set에 대한 Schedulable Utilization Bound]
Task Set ${\tau_1, \dots, \tau_n}$의 임의의 $p_i \ge p_j$에 대해, $mod(p_i, p_j) = 0$인 경우, utilization이 1 이하이면 schedulable하다.

pf)

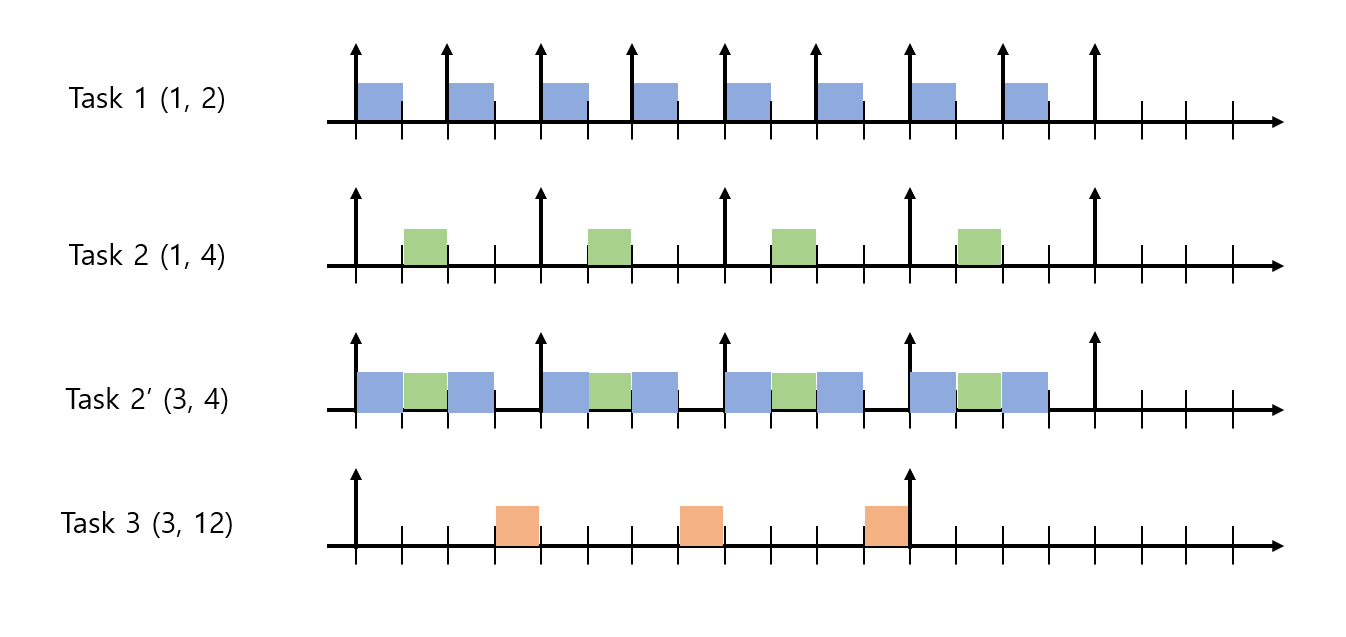
모든 period가 정수배이므로, $\tau_1, \dots, \tau_k$에 대해 $p_1, \dots, p_{k-1}$는 모두 $p_k$의 약수이고 따라서 hyperperiod는 $p_k$이다.
따라서 먼저 $\tau_1, \tau_2$에 대해 생각해보면 $p_2$마다 실행되는 패턴이 반복적인 것을 알 수 있다. 이는 가장 period가 짧은 두 task이기 때문에 다른 task에 preemption당할 일이 없기 때문이다. 그럼 두 task를 합쳐서 $p_2$마다 $e_1 + e_2$만큼 실행되어야 하는 task가 대신 있다고 해도 실행 패턴은 동일하다. 그림에서는 Task 1, Task 2 대신 Task 2'이 있어도 동일하다. 이를 $\tau_n$까지 반복하게 되면, $\tau_n' (p_n, p_n)$이라는 task 하나만 남게 된다. 당연히 task가 한 개인 경우에는 utilization이 1이어도 schedulable하므로, harmonic task set에 대해서는 utilization이 1 이하이기만 하면 scehdulable하다.

기존 논문의 식에 대한 반례)
$\tau_1 = (1, 2), \tau_2 = (2.1, 5), \tau_3 = (0.8, 10)$으로 놓으면 모든 period가 10의 약수이지만 schedulable하지 않다.
여담으로 period가 위와 같은 경우에 대해 L&L bound보다 더 널널한 bound를 계산하는 방법에 대한 논문이 있다. 기회가 되면 그 논문도 소개하도록 하곘다.

Ref

• Liu, C. L., & Layland, J. W. (1973). Scheduling algorithms for multiprogramming in a hard-real-time environment. Journal of the ACM (JACM), 20(1), 46-61.