14 Tree - terminology
앞에서 배운 스택, 큐, 링크드리스트, 트리, 그래프 등 모두 데이터의 구조이고 어떤 목적을 가지고 데이터의 특성들을 반영하여 저장하는 방법
스택, 큐는 들어오는 순서
링크드리스트는 배열된 데이터들의 선후관계
Tree
하나이상의 노드들이 존재함
root가 되는 노드가 존재함
그리고 그 나머지들은 또 tree로 나뉘어진다. (또 root가 있고,,,의 구조)
-
subtree
T1의 모든 노드가 T2에 포함될 때 T1은 T2의 subtree라고 불린다 -
size of tree
= the number of nodes -
leaf
= degree가 0 -
degree
= 서브트리의 개수 -
트리의 degree =
트리에 있는 노드 중 최대 degree -
level of node (= depth of a node)
= root로부터 나까지 도달하는데에 걸리는 길이 -
Height (depth) of a tree
= maximum level of any node in the tree
= the length of the longest root-to-leaf path -
Width of a tree
= the size of the largest level
(largest = 가장 노드 수가 많은 레벨에 있는 개수) -
path
= 다음 단계 노드들을 쭉 적어놓는 거 (ex A - D - E - F) -
length of path
= the number of parent - child pairs -
k - ary tree
= degree of every node in a tree is k
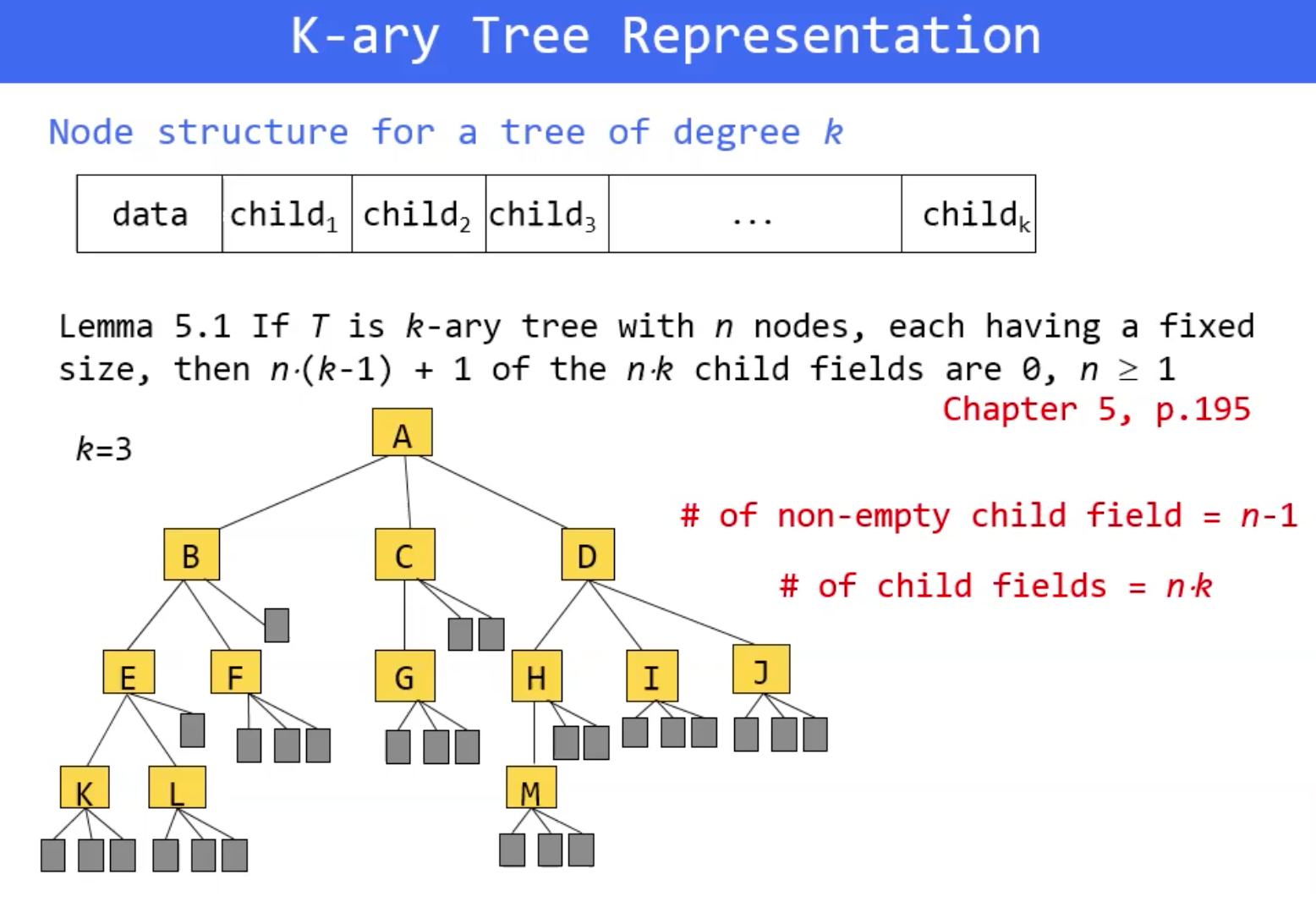
k - ary tree
트리상에 노드는 그 노드가 표현해야할 데이터와 child의 포인터로 되어있음
k = 3이라면, 3개의 child와 노드의 데이터정보를 저장하는 구조
널 포인터가 아닌 것의 개수 : n-1
(왜?? -> root는 자기 자신을 가리키는 포인터가 없기 때문에)
n개의 노드가 모든 이런 구조가 되어있고 child field = n * k
data는 이런식으로 구조화 됨
data의 왼쪽에 있는 child를 저장하고, 오른쪽의 sibling을 저장.
예시로 A의 경우,
left child는 B, right sibling은 없기때문에 null
B의 경우
left child: E, right sibling: C인 것이다.
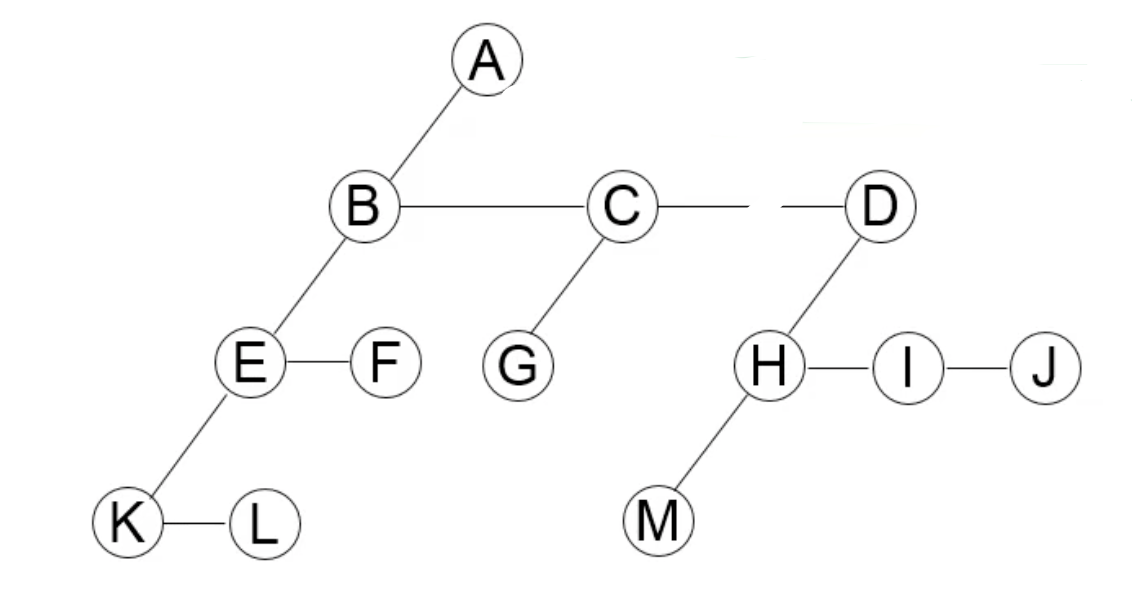
이런식으로 트리의 형태를 갖추게 됨
binary
left subtree, right subtree만을 가진 트리
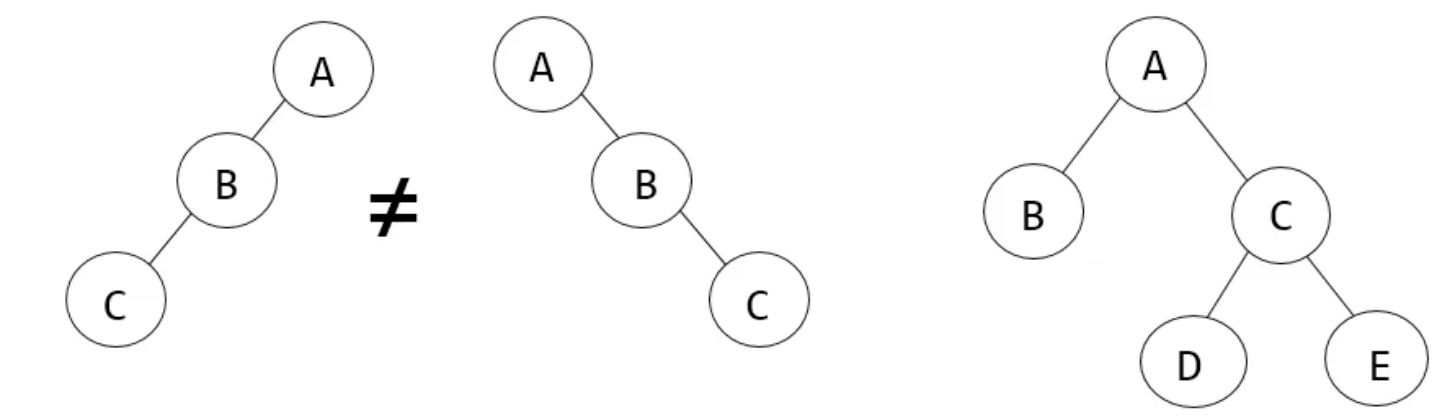
이러한 것들이 binary의 예시이고, 왼쪽과 오른쪽, 위아래 위계 관계가 트리에서는 중요하기 때문에 예시의 두 트리는 같다고 볼 수가 없다.
full binary tree
= 모든 degree가 꽉 찬 상태
full binary tree 판단하는 방법: 트리의 depth를 알아내고, 전체 노드의 개수를 알아내서 트리의 노드의 개수가 2^k-1 인지 확인, leaf 노드를 제외하고 모든 node의 degree가 동일한지 판단
complete binary tree:
full binary tree는 complete binary tree 이다.
complete binary tree는 full binary tree이지는 않는다.
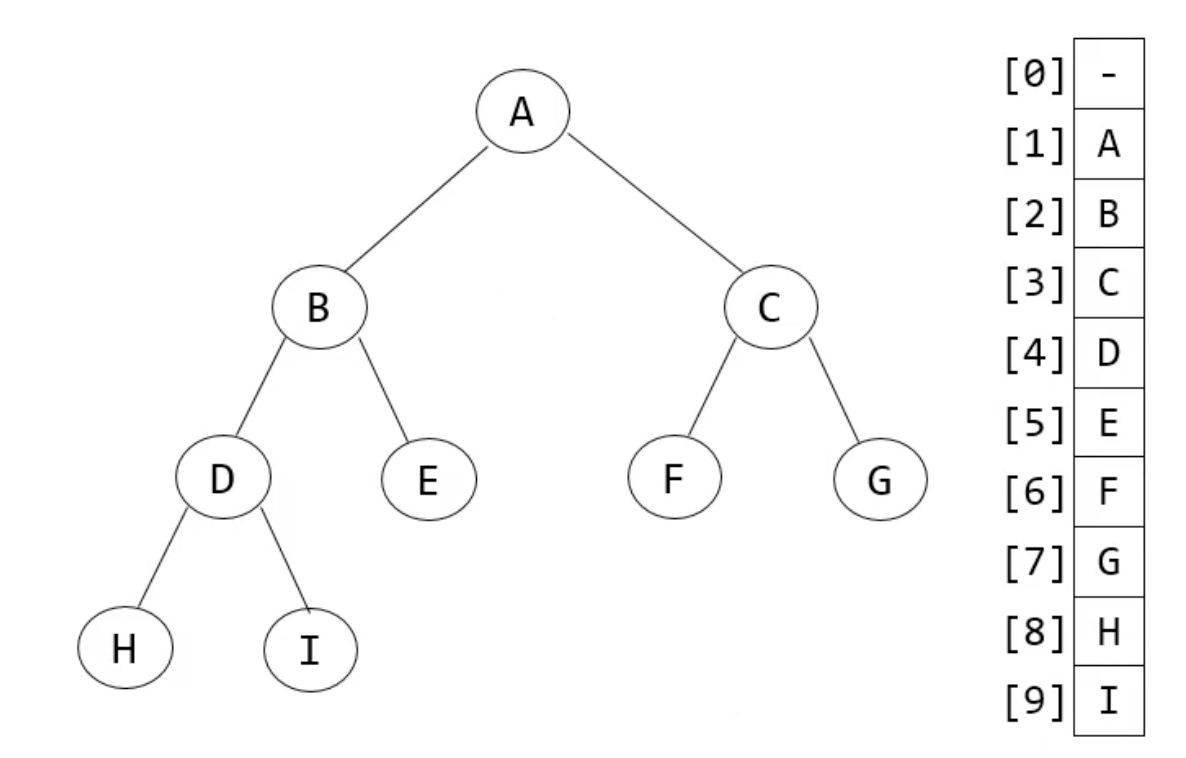
tree 표현식
- array ver.
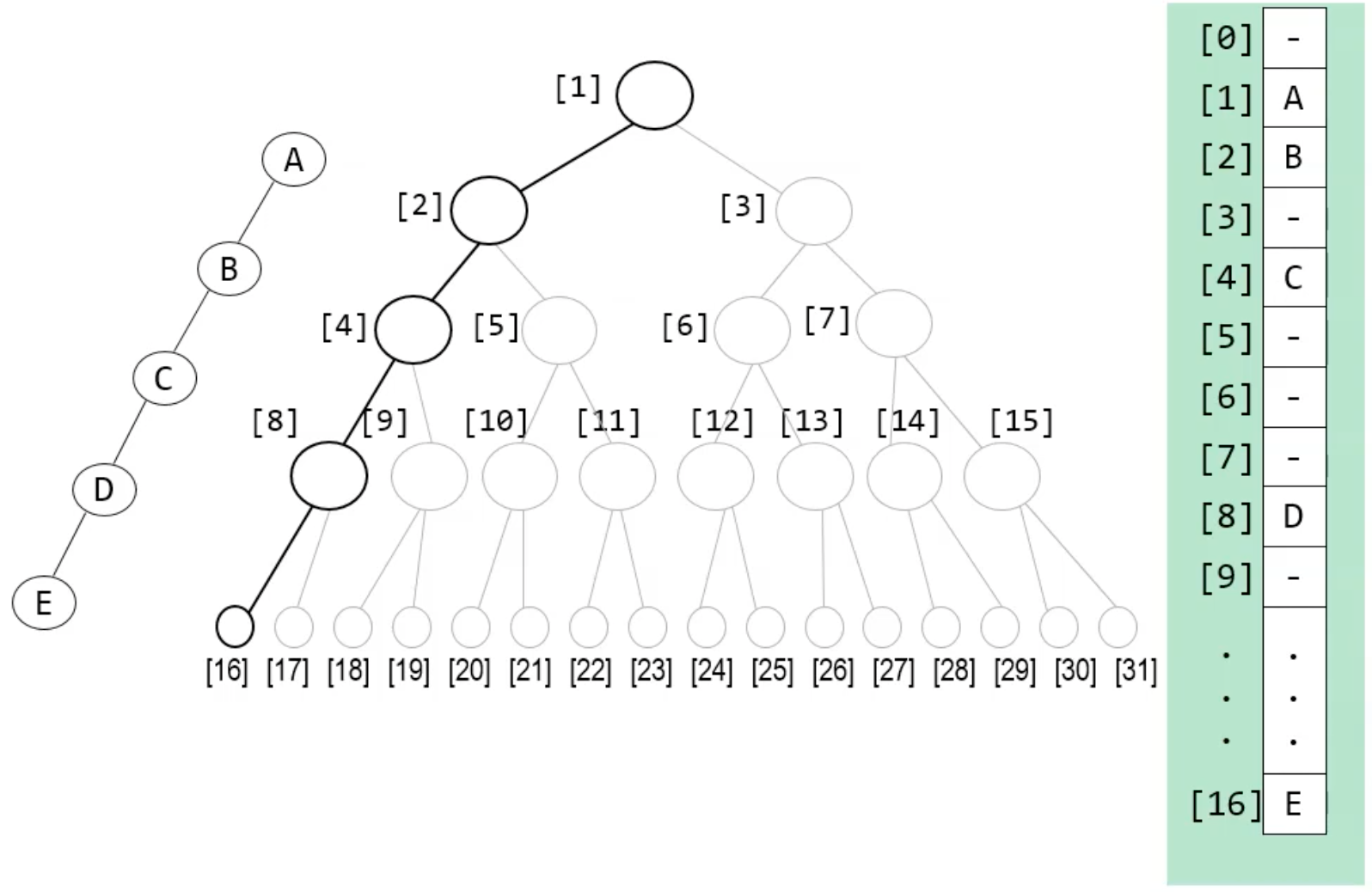
= 이렇게 한 쪽으로 치우친 트리는 array로 표현했을 때 낭비가 심하다는 것을 알 수 있음
- linked list ver.
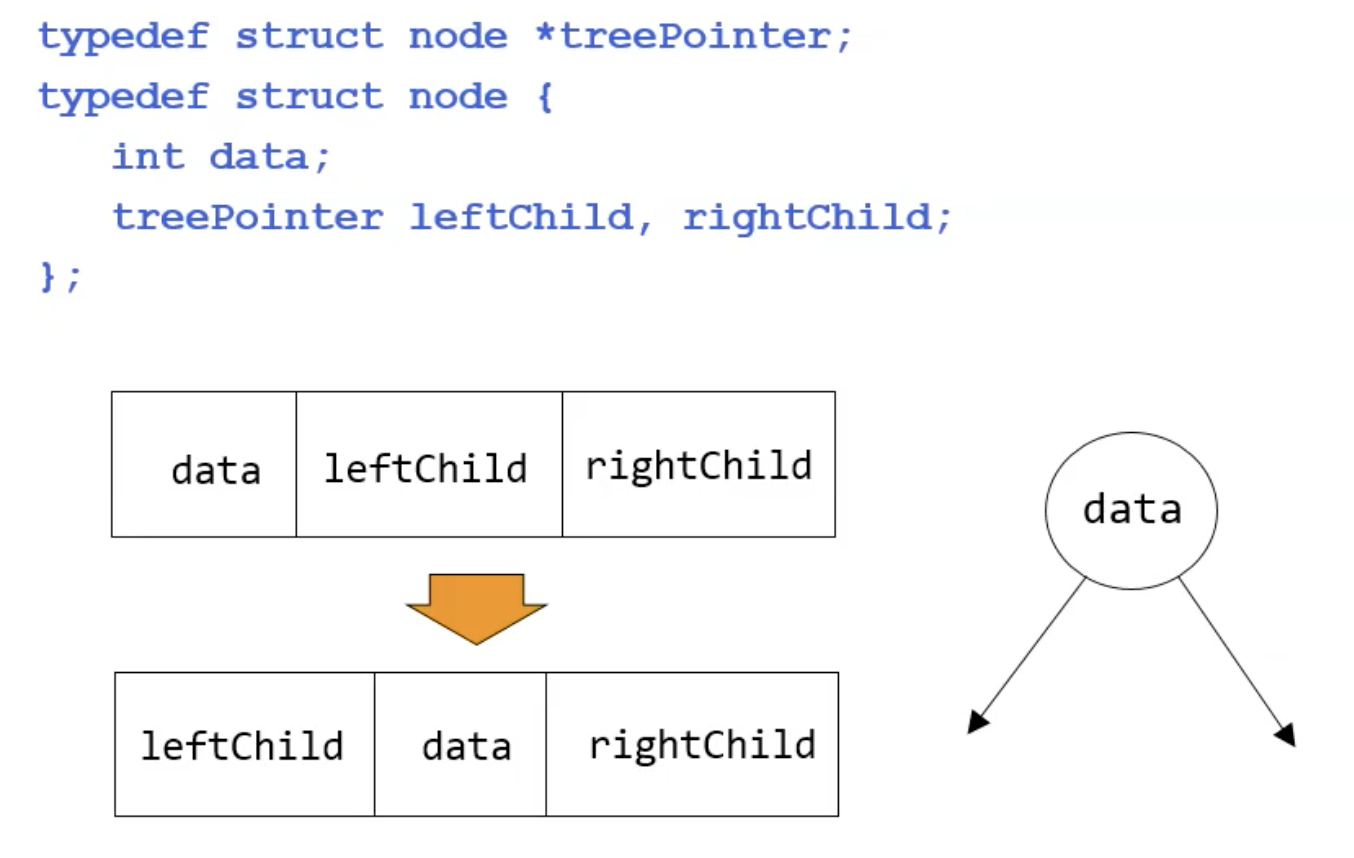
구조체 표현식을 data, leftchild, rightchild 순에서
leftchild,data,rightchild 순으로 구성하며 가독성을 높임!
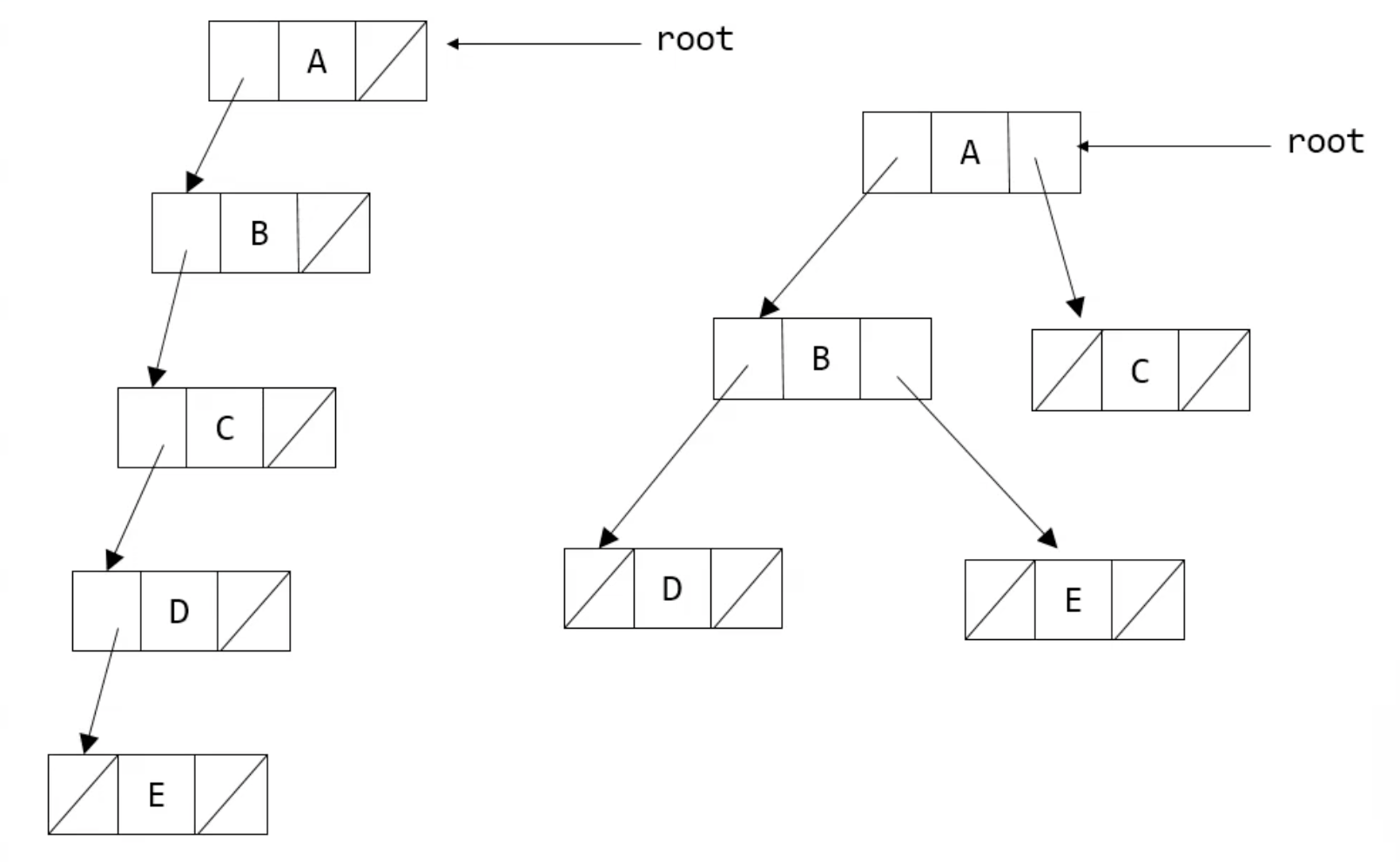= 링크리스트를 활용하면 한쪽으로 치우친 트리 모양의 경우 훨씬 표현하기가 쉬움
후,,, 링크리스트 걍 빠르게 건너 뛸걸,,,, 트리하니까 바로 이해되네 ㅠ
