자료구조 | Matrix

21/06/11 아니 계획상 basic이 끝났어야 했는데 작심삼일도 못했다니!

Basic - 5. Matrix

행렬(Matrix): 데이터들이 2차원 형태로 저장되어 있는 것.
그렇기 때문에 가장 쉬운 표현 방법은 2차원배열 형태로 직관적 표현하기. index 상으로 행렬 매겨서 해당하는 값 선언하는 상황

Sparse Matrix : 의미 있는 행렬이 드문드문 존재하는 것

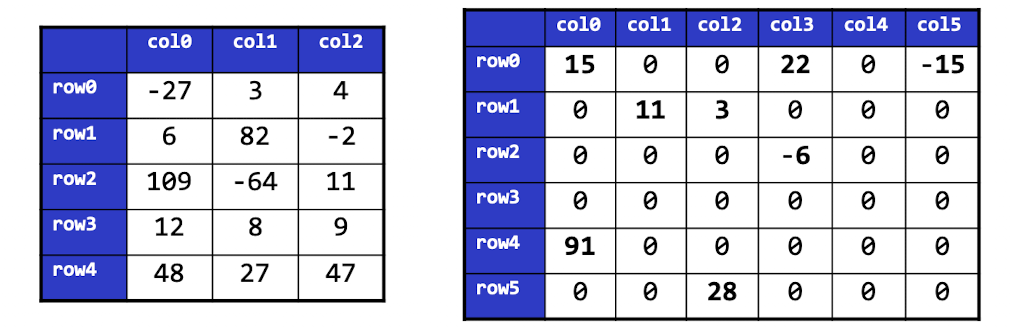
-> (1) 15/15 // (2) 8/36 = sparse matrix

의미 있는 값이 별로 없는 행렬(sparse matrix)인 경우에는? (자원대비 효율 중요)

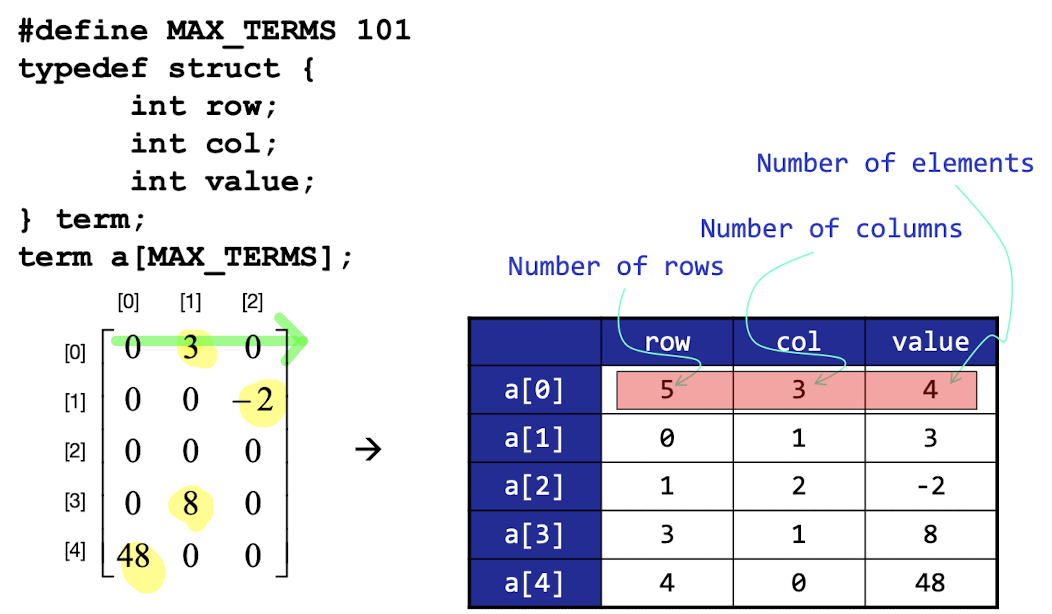
표현 방식: Term 이라는 데이터타입을 선언하여 그 안의 배열 생
순서: 맨 첫번째 row부터 맨 왼쪽에 있는 column부터 저장
값 저장 방식: 0번 index - row의 개수, col의 개수, 그리고 값을 가지고 있는 유의미한 값들이 몇 개인지의 개수
그 다음 index - 몇번째 row, 몇번째 col에 몇이라는 값이 있는지를 저장
ex) a[1] => [0][1] 위치에 3이라는 값 존재

Transpose
(i,j) -> (j,i)
row와 col 값을 바꾸는 법

각각의 row에 대해 (i,j,value)를 (j,i,value)로 바꾸면 되는 거 아닌가? -> row,col,value 로 저장하고자 했던 방식 자체가 깨지는 것임.

원래 매트릭스에서의 col에 대해 0번 col 값 -> 0번 row, 1번 col값 -> 1번 row 식으로 옮기기

row를 쭉 스캔 하면서 0번째 값부터 row에다가 저장하는 순서로 진행하는 방법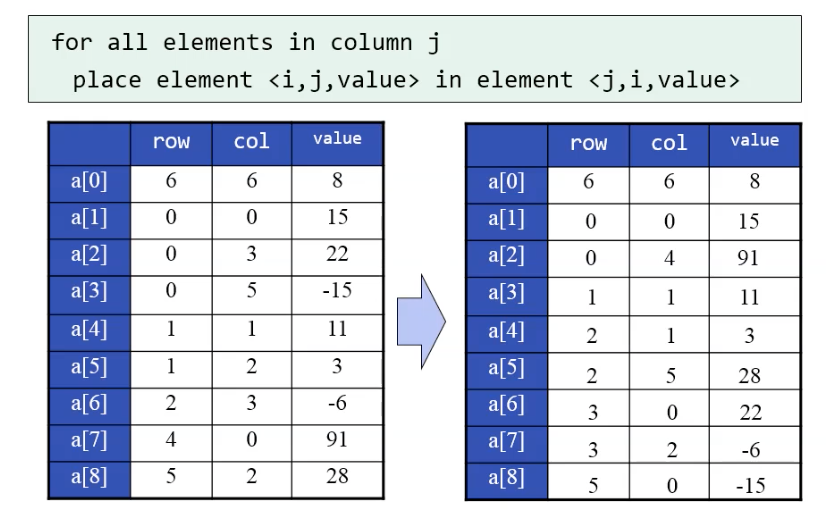

void transpose(term a[], term b[]) {
// a - original , b - new array 
int n, i, j, currentb;
n = a[0].value; //모든 elements의 총개수
b[0].row = a[0].col; //a에 있는 col -> b에 있는 row
b[0].col = a[0].row; //a에 있는 row -> b에 있는 col
b[0].value = n; //b[0].value = a[0].value;를 간소화
if (n > 0) { // value 가 0인 빈공간이 아니라면
currentb = 1;
for (i = 0; i<a[0]col; i++){ //col값 증가시키면서
	for(j= 1; j<= n; j++{
		if(a[j].col == i) //i값과 같은 a의 col 값이 있다면
		  b[currentb].row = a[j].col;
		  b[currentb].col = a[j].row;
		  b[currentb].value = a[j].value;
		  currentb++; //찾으면 swap
      }
}
}
}

Time complexity => O(colums * elements)
최적화 x , 매우 복잡~,~

Fast matrix Transpose

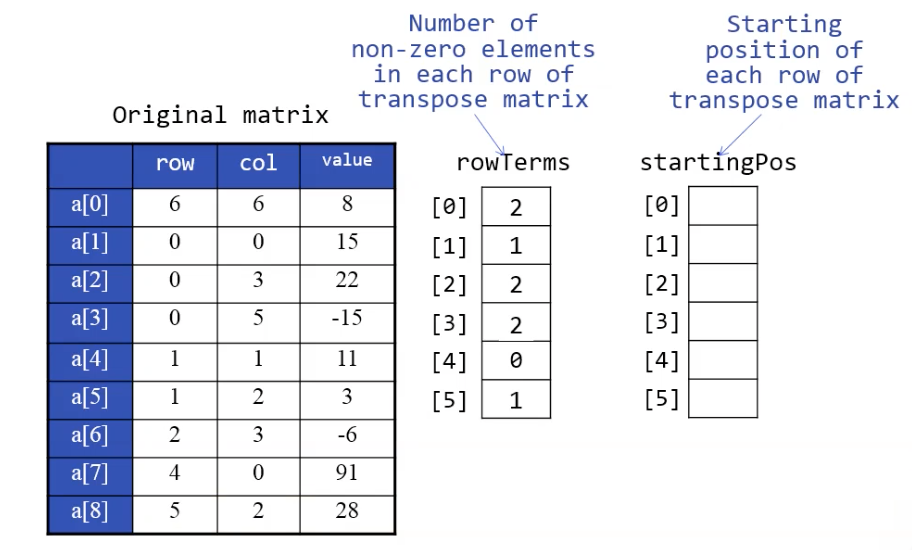
for(i = 1; i<=numTerms; i++) {
    rowTersms [a[i].col]++;
}

RowTerms
미리 몇번째 col에 값이 저장되어있는지 한번 쭉 스캐닝하고 그 값들을 저장할 배열을 생성하여 값을 넣는 과정을 추가한다.

startingPos[0] = 1;
for(i = 1; i<num_cols; i++) {
   startingPos[i] =
    	startingPos[i-1]+
        rowTerms[i-1];
}

StartingPos
0번 index에는 row의 개수, col의 개수, 값을 가진 수의 개수가 저장되어 있기 때문에

StartingPos[0] = 1

그후

for (i = 1; i<num_cols; i++) {
  startingPos[i] =
   startingPos[i-1] + rowTerms[i-1];
 }

StartingPos는 rowTerms에서 미리 몇 번째 위치에 col이 저장되어 있는지 확인했고, 그 위치 다음의 시작점을 표시해주는 배열이다.

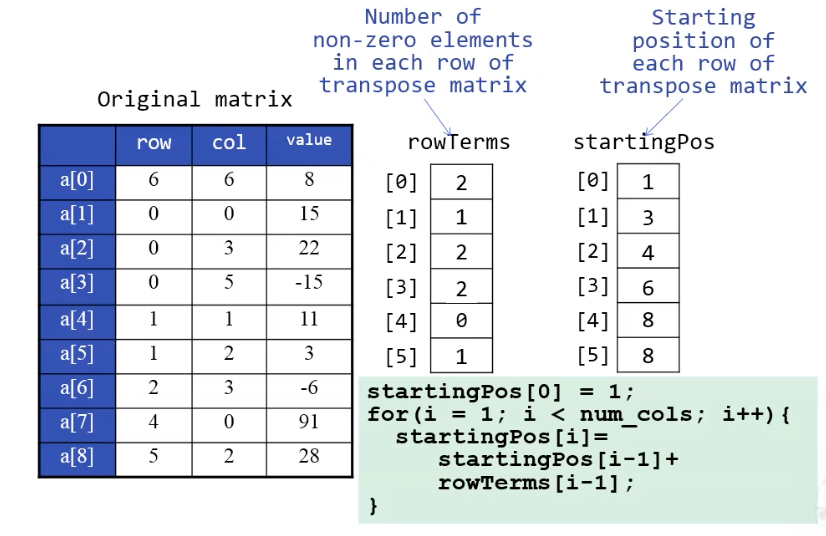
a[2]: <0,3,22> -> b[startingPos[3]]: <3,0,22>영상: 36분 ~

time complexity = O (columns + elements)

void fastTranspose(term a[], term b[])
{
int rowTerms[Max_COL], startingPos[MAX_COL];
int i,j,numCols = a[0].col, numTerms = a[0].value;
b[0].row = numCols;
b[0].col = a[0].row;
b[0].value = numTerms;
if (numTerms > 0) {
	for(i=0; i< numCols; i++) {
      rowTerms[i] = 0;
      }
      for(i=1; i<=numTerms; i++) {
      rowTerms[a[i].col]++;
      }
      startingPos[0] = 1;
      for(i = 1; i < numCols; i++) {
      	startingPos[i] = startingPos[i-1] +rowTerms[i-1];
        }
       for(i = 1; i<= numTerms; i++) {
       		j = startingPos[a[i].col]++;
            b[j].row = a[i].col;
            b[j].col = a[i].row;
            b[j].value = a[i].value;
            }
      
	}
}