Merge sort 병합정렬 합병정렬
병합정렬은 존 폰 노이만이 1945년에 고안한 정렬방법론이다.
분할정복 알고리즘을 기반으로 하는 정렬방법이다.
병합정렬은 안전한 정렬(stable sort)이다. 여기서 안전하다는 뜻은
같은 비교수의 원소가 2개이상 존재할때, 한번 앞에 있었던 원소는 같은 값들 사이에서 계속 앞에 있게 된다.
이게 무슨 말인고 하니 쉽게 설명하자면 아래의 배열을 먼저 보자.

우리는 위의 배열을 나이순대로 정렬하려고 한다.==(정렬 기법을 모르면 결과를 예측할 수 없다.)==
위 배열을 병합정렬로 정렬하면 21살 중에서 반드시 송아름이 제일 먼저 위치한다.
21살인 사람들만 보자면 송아름,박예린,이보나 순서로 나올 것이다. 이게 안전한 정렬을 뜻한다.
반대로 퀵정렬(QuickSort)는 안전한 정렬이 아니다.
병합정렬의 원리는 분할정복을 기반으로 한다고 위에서 설명하였다.
컴퓨터 알고리즘에서 분할이라고 하면 통상적으로 반으로(이분) 나누는 것을 뜻한다.
병합 정렬은 병합 이라는 프로시저를 이용해 정렬 하는 기법인데, 이에 분할정복을 통해 정렬하는 빠른 정렬 기법이다.
==(병합이란 정렬된 두 배열을 정렬된 하나의 배열로 합치는 작업을 뜻한다.)==
분할의 예시를 보면 아래와 같다.
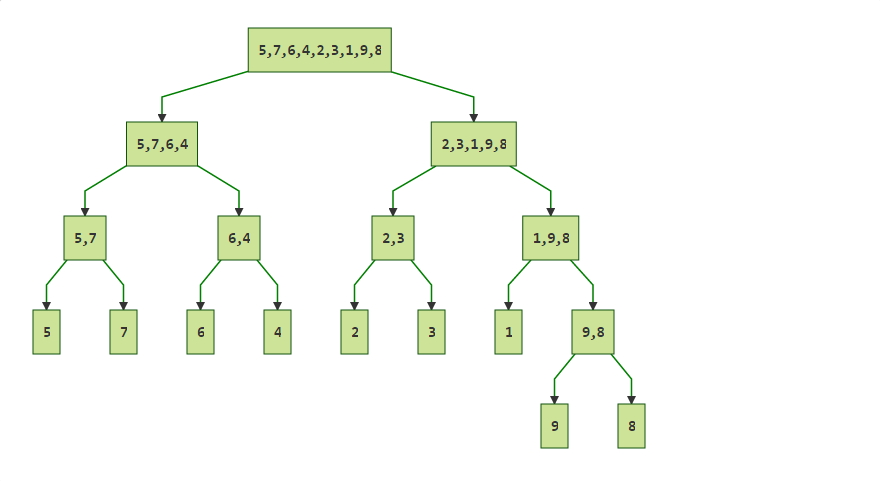
배열을 더 이상 분할할 수 없을때 까지 분할한후, 다시 역분할 즉, 정복하는 과정을 마치면 정렬이 된다.
정복의 과정은 2개의 배열을 병합 작업을 통해 하나로 합치는 작업이다.
위 그림에서 보듯이 각 층에서 병합작업에서 O(n)이 소요되고, 층의 높이는 lg(n)이 되므로 복잡도는 정확하게 nlgn이 나오게 된다.
실제로 병합정렬은 최선,최악의 경우가 없다.
보통 nlgn 정렬하면 퀵정렬, 병합정렬, 힙정렬이 있는데,
각각을 구분해보면 아래와 같다.
퀵정렬,힙정렬 : 안전하지 않음 , 추가 공간 필요없음
병합정렬 : 안전함 , 추가공간 필요함
힙정렬,병합정렬 : 복잡도가 일정함
퀵정렬 : 완벽하게 일정하지 않음==(퀵정렬 최악의경우 n^2가 나오는데 이건 개선안된방법이고, 개선해도 일정하진 않다 수학적으로)==
힙정렬은 단순 배열 정렬에서는 조금 그렇다. 같은 nlgn이라도 매우 느리다.
그렇다면 이제 C로 구현한 Merge 프로시저 부터 한번 보도록 하자.
==당연히 stdlib.h의 qsort에 대항하기 위해 만든것으로 제네릭하며 인터페이스 또한 qsort와 같다.==
씨언어에서의 Generic구현 방식을 이해해야 본 소스를 쉽게 이해할 수 있다.
void merge(char* fbegin, char* fend, char* sbegin, char* send, char* dst,
size_t size, int(*compar)(const void*, const void*))
{
int i = 0, j = 0, k = 0;
int it;
while (fbegin != fend && sbegin != send){
if (compar(fbegin, sbegin) < 0)
for (it = 0; it < size; it++)
*dst++ = *fbegin++;
else
for (it = 0; it < size; it++)
*dst++ = *sbegin++;
}
if (fbegin != fend)
memcpy(dst, fbegin, fend - fbegin);
if (sbegin != send)
memcpy(dst, sbegin, send - sbegin);
}반복자 형태로 순회하여 크기에 맞게 복사하는 Merge 함수이다.
메모리 복사를 memcpy를 쓰지 않고 char*로 대입하는 과정을 주목하라.
복사 메모리가 작다면 memcpy호출 비용보다 저 방식이 더 빠르다.
남은 Merge공간은 한번에 처리하는 memcpy함수가 좀더 유리하다.
그럼 이제 mergesort 부분을 보자.
void msort(void* base, size_t nmembs, size_t size, int(*compar)(const void*, const void*)) {
char* temp = (char*)calloc(nmembs, size);
char* p = (char*)base;
char* q = temp;
char* pt;
int m = 1;
int idx = 0;
while (m < nmembs){
for (idx = 0; idx < nmembs; idx += (m << 1)){
int fsz = m;
int ssz = m;
if (nmembs - idx < m * 2){
ssz = nmembs - (idx + m);
if (nmembs - idx < m){
fsz = nmembs - idx;
ssz = 0;
}
}
merge(p + idx*size, p + (idx + fsz)*size, p + (idx + m)*size,
p + (idx + m + ssz)*size, q + idx*size, size, compar);
}
m <<= 1;
pt = p;
p = q;
q = pt;
}
if (p != base){
memcpy(base, p, nmembs*size);
}
}당연하다면 당연하겠지만, 메모리 복사,할당 오버헤드를 줄이기위해 포인터 스왑을 사용한다.
병합정렬은 재귀함수로 짤 필요가 없다.
이 부분에 대해 좀더 자세히 설명을 하자면, 정렬 라이브러리는 속도가 최우선인 라이브러리라고 생각한다.
속도와 공간적인 면을 볼때 반복이 재귀함수보다 안좋은면은 단 한개도 없다.
일반적으로 재귀함수를 반복문으로 바꾸려면 Stack이 필요한데, 이 병합정렬은 그 예외에 해당한다.
이 예외란, 스택에 저장할 정보를 계산으로 대치가 가능할때 스택이 필요없어지는 현상이 발생한다.
예를들면 GCD함수 등....MergeSort는 반드시 1/2로 쪼개기 때문에 쪼개지는 위치를 계산으로 대치할 수 있다.
==(위의 소스에서는 변수 m이 그 역할이다.)==
반복으로 구현함에 있어서 m이 2의 n이 아닐때의 예외는 if문으로 처리한다.
Merge와 MergeSort 모두 char ptr 를 사용하는데, C에서 배열을 제네릭하게 다룰때는 void ptr를 사용하지 않는다.
==(해보면 안다. 어차피 char로 형변환 하는데 뭣하러 void를 계속 쓰는가?)==
아래는 qsort 와 msort의 비교 결과이다.
OS : Windows10 x64
VS 2013 DEBUG 데이터 100만개
array size : 1000000
Random
qsort : 0.463700
msort : 0.334100
Sorted
qsort : 0.443200
msort : 0.340100
Reversed
qsort : 0.438300
msort : 0.333300VS 2013 RELEASE 데이터 1000만개
array size : 10000000
Random
qsort : 0.703200
msort : 0.570400
Sorted
qsort : 0.546500
msort : 0.569200
Reversed
qsort : 0.547300
msort : 0.566900RELEASE 모드에서 정렬된 경우와 역순일때 qsort보다 0.02초 정도 밀리는데, 이는 근소한 차이라 무시해도 되고..
DEBUG모드에서는 msort가 압도하였고, RELEASE에서도 Random한 경우에서는 해당 msort가 압도한다.
당연히 C의 qsort는 기본 퀵정렬이 아니다.
최악의 경우에 n^2이 나온다는 이런 소리는 C언어를 공부했다면 제발 하지말자. (간단한 테스트로 증명되잖아)
#####이제 C의 정식컴파일러인 gcc에서 비교를 해보자
OS : Windows10 x64
gcc 4.9.2 o0 데이터 100만개
array size : 1000000
Random
qsort : 0.063800
msort : 0.117600
Sorted
qsort : 0.053500
msort : 0.120800
Reversed
qsort : 0.053300
msort : 0.119900gcc 4.9.2 o2 데이터 100만개
array size : 10000000
Random
qsort : 0.729400
msort : 1.456600
Sorted
qsort : 0.587800
msort : 1.444600
Reversed
qsort : 0.588500
msort : 1.446200아니 이자식이???
장난 하는것도 아니고, 차이가 너무난다. ㅡ,ㅡ;
내가 볼땐 100만개 일땐 측정결과가 10개 차이가나 감을 잡을 수 없고, 1000만개일때를 보면
qsort는 VS나 gcc나 비슷한데, 내 msort만 느리게 나오는걸 보니, 컴파일러 최적화가 VS보다는 못하다는걸 알 수 있다.
지들 qsort만 최적화를 겁나 해놓았나 봄
그렇다면 왜 사람들이 일반적으로 quick sort가 merge sort 보다 빠른 경우가 더 많다고 할까?
해답은 간단하다. MergeSort는 memory write가 quicksort에 비해 많이 발생한다.
QuickSort는 nlgn 보다 빨리 결과가 나오는 경우도 있다.
내가 볼땐 둘중에 뭐가 더 빠르냐 라는 질문은 이제 거의 의미가 없는듯 하다.
정렬알고리즘은 이미 시간적인 면에 있어서 충분히 하한적으로 발전했다.
C언어에서는 Merge가 없습니다.(그래서 만들어 줬잖아)
C언어에서는 qsort를 사용할때 비교함수를 작성해야하는데, 단순히 앞에서 뒤에것을 빼는 사람들이 많네요.
만일 int자료형일때 앞의 값이 20억이고 뒤의 값이 -10억이면 둘의 차이는 30억이 되어 overflow가 나게 됩니다..
비교함수는 아래와 같이 짜야 합니다.
int cmp(const void* a, const void* b) {
return *(int*)a<*(int*)b ? -1 : *(int*)a>*(int*)b;
}C++에서는 merge sort가 있습니다.
std::stable_sort라고 하며, (앗! 이름이 stable sort구만 !!)
algorithm 헤더에 존재한다.
내부적으로 < 연산자로 비교를 한다.
#include<algorithm>
#include<functional>
#include<vector>
using namespace std;
struct Z{
int a;
char b;
Z(int _a, char _b) {
this->a = _a;
this->b = _b;
}
//const 함수인것에 유의해라 이거때문에 시간날린적이 많다.정확하게 오버로딩 해야한다.
bool operator<(const Z& z)const {
return this->a < z.a;
}
};
int main() {
vector<int> v;
for (int i = 0; i < 100; i++){
v.push_back(i);
}
random_shuffle(v.begin(), v.end());
stable_sort(v.begin(), v.end());
//자료형이 기본자료형,기본클래스 일경우 3번째 비교자 생략가능
stable_sort(v.begin(), v.end(),less<int>());
//위의 문장과 완벽히 같다.
stable_sort(v.begin(), v.end(), greater<int>());
//역순으로 정렬하는 예제 (less,greater는 함수 객체로 functional에 포함)
vector<Z> z;
for (int i = 0; i < 100; i++){
z.push_back(Z(i, 'a'));
}
random_shuffle(z.begin(), z.end());
stable_sort(z.begin(), z.end());
//클래스이고 비교자가 없을경우 < 연산자 오버로딩을 참조한다.
return 0;
}Perl에는 sort가 있긴한데...이놈은 quick sort 입니다. MergeSort는...
use sort '_mergesort'; #나는 머지 소트를 쓰겠다는 뜻
my @a=(2,5,1,3,4);
@a=sort @a; #머지 소트로 동작한다.Pascal에는 버블정렬도 없어요 ㅠ.ㅠ
그래서 Pascal 전용 MergeSort를 만들었습니다.
type
itype=longint;
intptr=array of itype;
procedure merge(first:intptr;fbgn:longint;fsz:longint;second:intptr;sbgn:longint;ssz:longint;dst:intptr;dbgn:longint);
var i,j,k:longint;
begin
i:=fbgn;
j:=sbgn;
k:=dbgn;
while((i<fsz) and (j<ssz))do
begin
if(first[i]<second[j])then
begin
dst[k]:=first[i];
i:=i+1;
end
else
begin
dst[k]:=second[j];
j:=j+1;
end;
k:=k+1;
end;
while(i<fsz)do
begin
dst[k]:=first[i];
i:=i+1;
k:=k+1;
end;
while(j<ssz)do
begin
dst[k]:=second[j];
j:=j+1;
k:=k+1;
end;
end;
procedure merge_sort(var base:intptr);
var
temp,p,q,tmp:intptr;
m,idx:longint;
fsz,ssz:longint;
len:longint;
begin
len:=length(base);
SetLength(temp,len);
p:=base;
q:=temp;
m:=1;
while(m<len)do
begin
idx:=0;
while(idx<len)do
begin
fsz:=m;
ssz:=m;
if(len-idx<m*2)then
ssz:=length(base)-idx-m;
if(len-idx<m)then
begin
fsz:=len-idx;
ssz:=0;
end;
merge(p,idx,fsz+idx,p,idx+m,ssz+idx+m,q,idx);
idx:=idx+m*2;
end;
m:=m*2;
tmp:=p;
p:=q;
q:=tmp;
end;
if(p<>base)then
for m:=0 to len-1 do
base[m]:=p[m];
end;다른 언어는요?
직접 짜보세요.

