Cyclical Learning Rates for Training Neural Networks

CLR(Cyclic Learning Rates)는 최근 Kaggle과 같은 대회에서 성능을 극한으로 올리는데 유명한 기법중 하나이다.

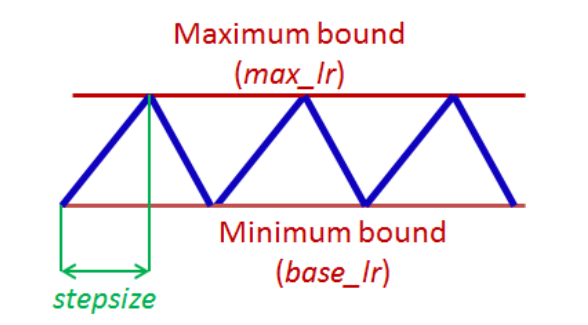
그림으로 보면 이해가 쉽다. stepsize에 따라서 올라갔다 내려갔다 한다.

코드로 구현하면 아래와 같다.

def CyclicLearningRate(initial_learning_rate, maximal_learning_rate, step_size):
    def _CyclicLearningRate(iter):
        value = iter % step_size
        if (iter // step_size) % 2 == 0:  # increase
            return (initial_learning_rate + maximal_learning_rate) / step_size * value
        else:  # decrease
            return maximal_learning_rate - ((initial_learning_rate + maximal_learning_rate) / step_size * value)

    return _CyclicLearningRate

clr_f = CyclicLearningRate(0.0001, 0.001, 20)
data = []
for i in range(400):
    data.append(clr_f(i))
plt.plot(data)

plt.ylabel('learning rate')
plt.xlabel('epoch')

plt.show()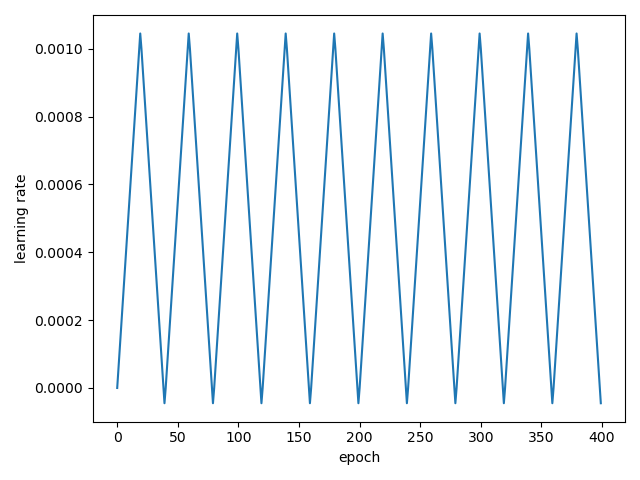

tensorflow_addons

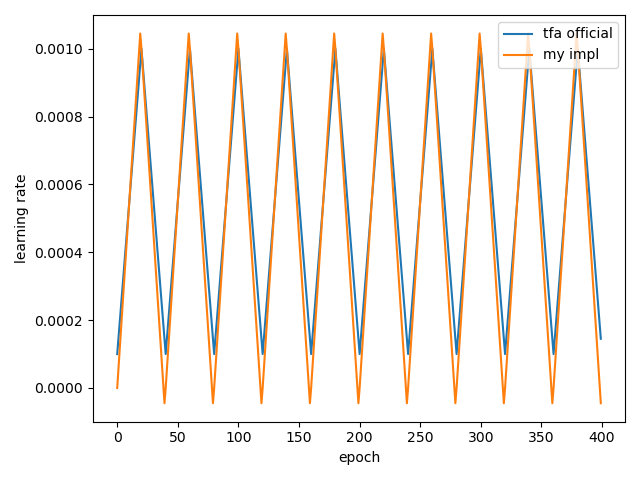
이 기능은 Tensorflow_addons에서도 제공하고 있다. 아래는 내가 만든 CLR과 TFA의 CLA를 비교한건데 차이가 있지만 큰 차이는 보이지 않는다.

이제 scale_fn을 적용해보자. 이게 iter단위로 적용되는줄 알았는데 TFA에서는 step단위에서 적용된다. 아래의 코드와 결과를 보자.

import tensorflow as tf
import tensorflow_addons as tfa
import matplotlib.pyplot as plt
import math


def triangle_fn1(x):
    return 1. / (2. ** (x - 1))


def CyclicLearningRate(initial_learning_rate, maximal_learning_rate, step_size, scale_fn):
    def _CyclicLearningRate(iter):
        value = iter % step_size
        if (iter // step_size) % 2 == 0:  # increase
            lr = (initial_learning_rate + maximal_learning_rate) / step_size * value
        else:  # decrease
            lr = maximal_learning_rate - ((initial_learning_rate + maximal_learning_rate) / step_size * value)
        return scale_fn(iter // step_size) * lr

    return _CyclicLearningRate


clr_f = tfa.optimizers.CyclicalLearningRate(
        initial_learning_rate=0.0001,
        maximal_learning_rate=0.001,
        step_size=20,
        scale_fn=triangle_fn1,
)
clr_f2 = CyclicLearningRate(0.0001, 0.001, 20, triangle_fn1)
data = []
data2 = []
for i in range(400):
    data.append(clr_f(i))
    data2.append(clr_f2(i))
plt.plot(data)
plt.plot(data2)
plt.legend(['tfa official',
            'my impl',
            ], loc='upper right')
plt.ylabel('learning rate')
plt.xlabel('epoch')

plt.show()

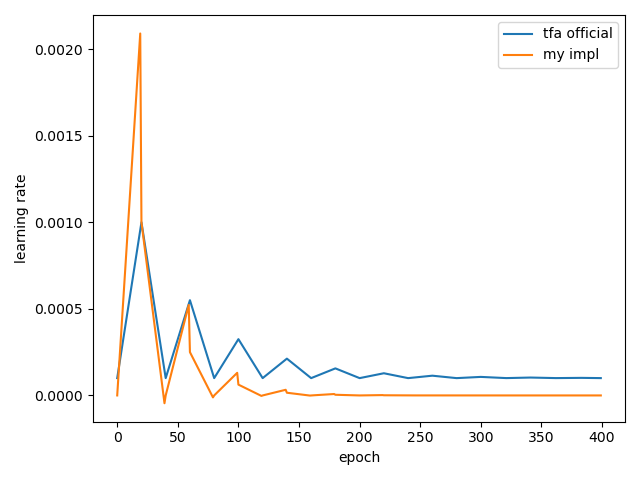
봐줄만한 수준이다. 비슷하게 가고 있다. 조금씩 다른 이유는 알아서 찾아보길 바란다.

결국 원하는건 LR이 커졌다 작아졌다 하면서 결국에는 수렴하는 결과를 원한다. 이에 대해 traingle_fn1은 좋은 결과를 보였고 해당 수식은 아래와 같다.

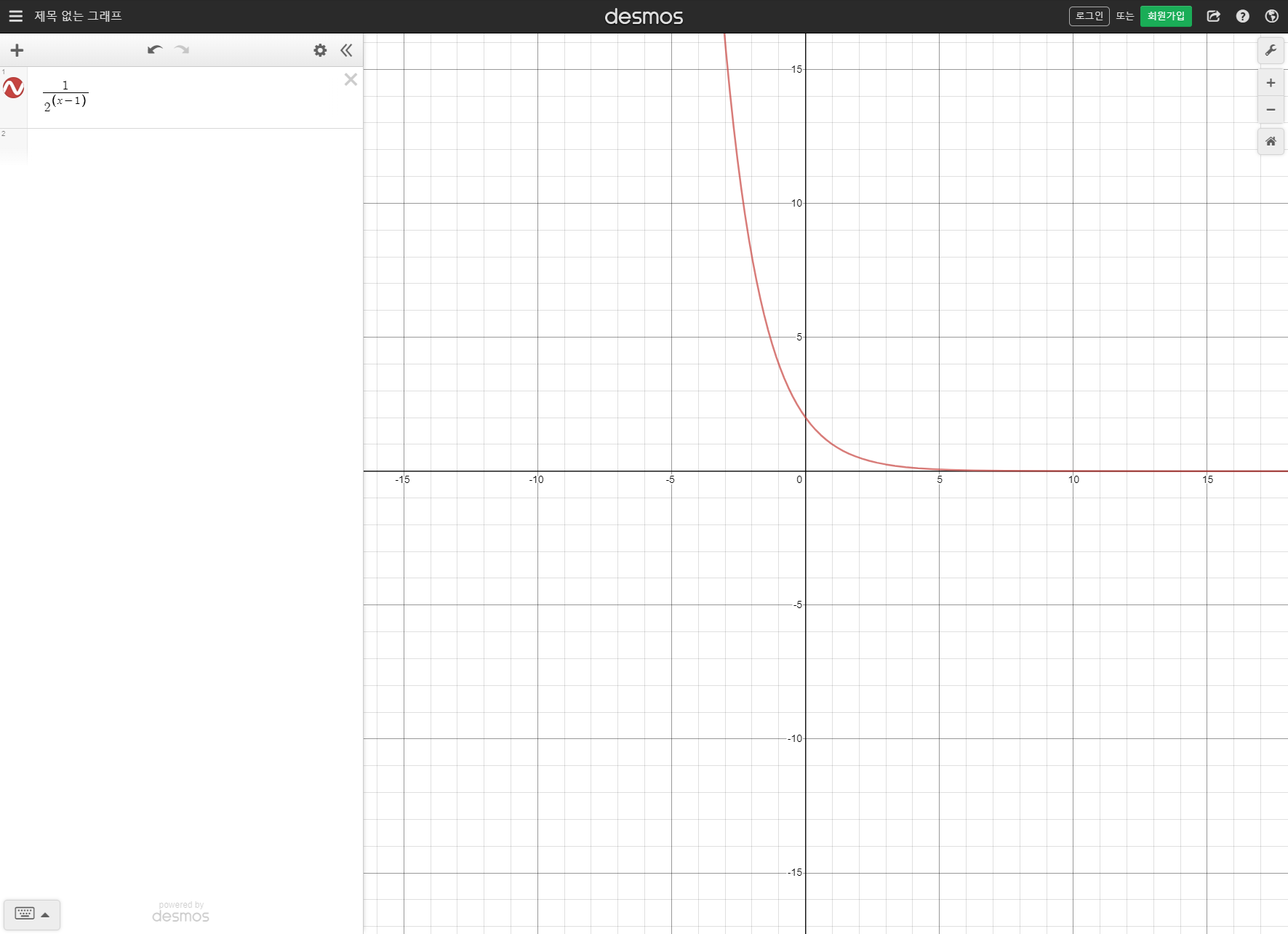
하지만 처음에 제안한 traingle_fn1은 너무 빨리 수렴하느 문제가 있어서 조금 더 수정하면 아래와 같이 구현할 수 있다.

def triangle_fn2(x):
    return 1. / ((1 / math.log(2)) ** (x - 1))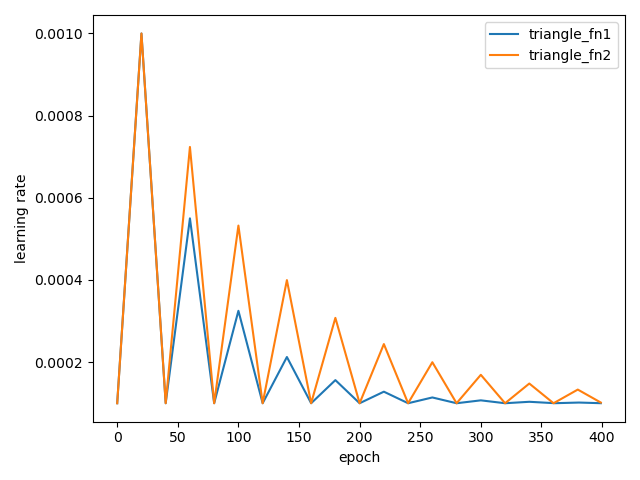

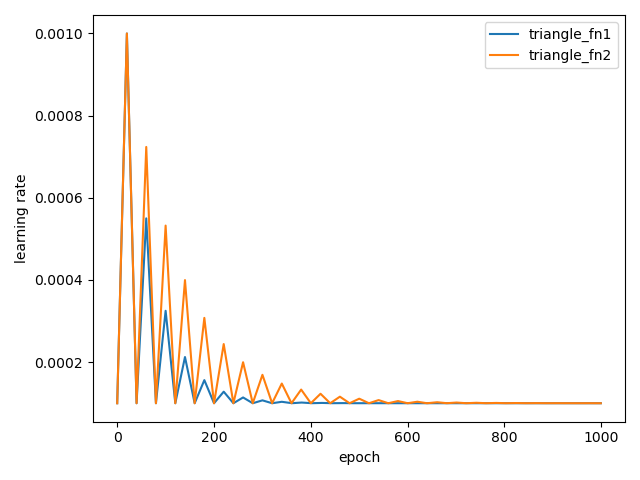
많은 epoch를 수행할 때 더 많은 CLR의 효과를 볼 수 있다. Epoch에 따라서 다르게 지정하여 사용하면 될 것 같다.