여태까지 DFS, BFS를 공부했다.
최단거리를 구하는데 BFS가 매우 적합하지만,
BFS로 최단거리를 구하지 못하는 문제도 존재한다고 한다.
구별하는 방법은 이동할 수 있는 거리에 비용이 붙어있는가이다.
바로 다익스트라 알고리즘이고,
다익스트라 문제를 몇개 풀어보고 문자열 문제들로 넘어가도록 한다.
최소비용은 벨만-포드, 플로이드워샬 알고리즘도 존재한다
다익스트라 - 시작점으로부터 끝점, 비용은 양수만
벨만포드 - 시작점으로부터 끝점, 음수도 됨
플로이드워셜 - 모든 정점간의 최소비용, 음수도 됨
https://riverrevir.github.io/2022/03/17/dijkstra.html
위의 문제집으로 다뤄본다.
1. 1753 - Dijkstra(Priority Queue)
https://www.acmicpc.net/problem/1753

다익스트라의 정석문제를 풀어보려고 한다.
자바로 풀어봤던 내용이고, CPP로 구현하면서 기억해본다.
영상을 참고하였다.
내용을 요약하자면,구현하는 방법에는 크게 2가지 방법이 존재한다.
하나는 정점간의 거리를 계산해두는 n^2배열의 표를 생성해두는 것,
다른 하나는 우선순위 큐를 사용하여
정점의 개수인 배열로 해당 정점까지의 최단거리를 갱신하는 것.이 중에서 후자가 좋은 이유가,
정점의 개수가 많아지는 경우, 전자로는 절대 못풀기 때문이다.
https://jungeu1509.github.io/algorithm/use-priorityqueue/
Priority Queue의 사용
그냥 큐처럼 사용하면, 큰 값부터 내림차순 정렬이 된다.
하지만, 그 기준을 오름차순으로 바꿀
해결
#include <iostream>
#include <vector>
#include <queue>
#include <limits>
#include <cstring>
using namespace std;
int v, e;
int start_v;
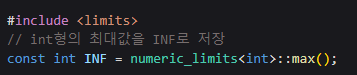
// int형의 최대값을 INF로 저장
const int INF = numeric_limits<int>::max();
int d[20001] = {
0,
};
vector<pair<int, int>> connection[20001]; // 가중치, 연결된 정점
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> v >> e;
cin >> start_v;
fill(d, d + v + 1, INF); // 배열을 d[0]~d[v]까지 INF로 채움
// 그래프 입력
while (e--)
{
int u, v, w;
cin >> u >> v >> w; // u와 v가 연결된 선의 가중치는 w
connection[u].push_back({w, v}); // w부터 저장하는 법 통일
}
// vector<pair<int, int> 구조에 pair<int, int> 자료형을 넣음 pair<int, int>를 오름차순
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
// 시작점 추가
d[start_v] = 0;
pq.push({d[start_v], start_v}); // 해당 점까지의 최단거리, (갈수있는 점)
while (!pq.empty())
{
// 1
auto cur = pq.top(); // pair<int, int>, pq의 가장 첫번째(*거리가 가장작은값)를 가져온다
pq.pop();
// 2
if (d[cur.second] != cur.first) // 현재 점까지의 최단거리가, 넣어진 거리와 다르다면, (d는 항상 최단거리만 저장한다)
{
continue; // 해당 경로를 더 갱신할 필요가 없으므로, 그냥 무시하고 queue를 다시 뽑음
}
// 3
for (auto nxt : connection[cur.second]) // 현재 점에 대한 연결들을 순회 // 가중치, 연결된 정점이 반환됨
{
if (d[nxt.second] <= d[cur.second] + nxt.first) // 현재 점을 통해 연결된 다음 점을 방문할때, d보다 크다면 갱신안함
{
continue;
}
else // 그렇지 않다면, 갱신함.
{
d[nxt.second] = d[cur.second] + nxt.first;
pq.push({d[nxt.second], nxt.second});
}
}
}
// 출력
for (int i = 1; i <= v; i++)
{
if (d[i] == INF)
{
cout << "INF\n";
}
else
{
cout << d[i] << "\n";
}
}
return 0;
}풀이
하긴했는데, 구조가 너무 복잡하다는 생각이 든다.
우선 priority queue가 가장 난해했다.
priority_queue
<
pair<int, int>,
vector<pair<int, int>>,
greater<pair<int, int>>
> pq;
A. Priority Queue
pair값이 들어가는 것도 이해했고, 마지막에 오름차순 정렬도 이해했는데,
왜 가운데 벡터가 들어가있는건지 이해가 안된다.
큐 내부에 존재하는 벡터인가??
벡터를 원소로 가지는 큐?
찾아보니 가운데 벡터가 주로 들어가게 되고,
벡터를 직접 사용하지는 않는다.
크게 의미두지말고,
Pair가 들어간 큐처럼 사용하는데 초점을 맞추자.
B. 동작원리
동작법은 BFS와 나름 유사하다.
// 1 - BFS처럼 queue에서 뽑는다
queue에 정점이름과, 현재시점의 정점까지의 최단거리를 넣는다.
queue가 빌때까지 뽑는다.
뽑는 순서는 현재 정점까지의 거리가 가장 짧은 것부터.
// 2 - 중간에 필요없는 작업을 컷한다
만약, 해당값이 현재 저장된 최단거리와 비교하여 다르다면,
(저장된 최단거리는 더 짧게끔만 최신화됨, 즉 더 길다면)
해당 거리로부터 이어지는 경로는 계산할 필요가 없으므로
다시 queue에서 뽑음 (Dijkstra가 음수를 계산할 수 없는 이유)
// 3 - 현재 점에 연결을 순회
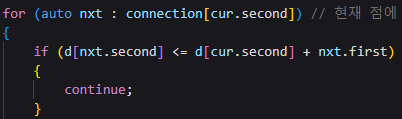
위의 기능이 가장 핵심이다.
해당 점에 대한 연결을 담은 Vector에서 nxt를 꺼내온다.
nxt는 pair값이다. 가중치와 해당 점의 이름.
따라서 저장된 연결된 점의 최소값보다,
현재점의 최소값 + 해당점까지의 가중치 가 더 작아야만
그 아래 코드를 실행하고, 갱신하고, 큐에 넣을 수 있게 된다.
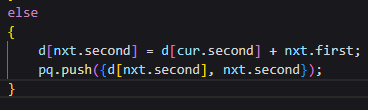
위의 갱신하는 시점에 cur에서 nxt위치로 이동했다는 정보를 저장하면,
Dijkstra로 최단경로를 구하는 것도 구현할 수 있다.
// 4 - BFS와 다르게 큐가 모두 빌 때까지 반복.
생각보다 간단한거같은데 구현실수가 나오기 딱 좋을만한
pair의 사용과 복잡한 선언방식이 아직 낯설다.
Dijkstra의 구현에 필수인 INF의 구현은 위처럼 했다.
일반 상수를 만들어 사용하는 것보다 위처럼 사용하는게 깔끔할 것 같다.
2. 11779 - Dijkstra
https://www.acmicpc.net/problem/11779
이전 문제의 심화버전이다.
각 점의 최단거리를 구하는것이 아니라, 도착도시까지의 최소비용이고,
추가로 최소비용의 경로를 출력해야한다.
해결
#include <iostream>
#include <queue>
#include <vector>
#include <limits>
#include <stack>
using namespace std;
const int INF = numeric_limits<int>::max();
int n_city, n_road;
int startIndex, endIndex;
vector<pair<int, int>> connection[1001];
int d[1001] = {0,};
int track[1001] = {0, };
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n_city;
cin >> n_road;
// INF로 채우기
fill(d, d+1001+1, INF);
// 입력
while(n_road--)
{
int a, b, w;
cin >> a >> b >> w;
connection[a].push_back({w, b});
}
cin >> startIndex >> endIndex;
// 반례 : 입력과 출력이 같은 경우
if(startIndex == endIndex)
{
cout << 0 << "\n";
cout << 1 << "\n";
cout << startIndex;
return 0;
}
// 큐 생성 및 초기화
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
d[startIndex] = 0;
pq.push({d[startIndex], startIndex});
while(!pq.empty())
{
int cur_Dist = pq.top().first;
int cur_Index = pq.top().second;
pq.pop();
if(d[cur_Index] != cur_Dist)
{
continue;
}
for(auto next : connection[cur_Index])
{
int next_Weight = next.first;
int next_Index = next.second;
if(d[next_Index] <= d[cur_Index] + next_Weight)
{
continue;
}
else //갱신
{
track[next_Index] = cur_Index; // track에 기록
d[next_Index] = d[cur_Index] + next_Weight;
pq.push({d[next_Index], next_Index});
}
}
}
// 출력
cout << d[endIndex] << "\n";
stack<int> trackPrint;
trackPrint.push(endIndex);
int count = 0;
int index = endIndex;
while(true)
{
if(track[index] != startIndex)
{
count++;
index = track[index];
trackPrint.push(index);
}
else
{
break;
}
}
trackPrint.push(startIndex);
cout << count+2 << "\n";
while(!trackPrint.empty())
{
cout << trackPrint.top() << " ";
trackPrint.pop();
}
return 0;
}풀이
기존의 Dijkstra 알고리즘을 그대로 구현하면 되었고,
경로를 구하는건, 단순히 자료구조를 하나 더 만들면 되었다.
track이라는 배열도 d가 갱신될때마다
같이 갱신되면서 해가 나올때 같이 완성되게 된다.
출력부분의 구현, 시작점이 끝점이랑 같은 경우
위의 2가지 부분만 추가로 고려하면 되는 문제였다.
슬슬 익숙해져간다.
3. 1504 - Dijkstra
https://www.acmicpc.net/problem/1504
1에서 N정점으로 이동할 때, 반드시 제시된 임의의 2개 정점을 거친
최단거리를 찾아내야만 한다.
내가 구현했던 Dijkstra 알고리즘으로
정점간 이동은, 가는게 비용이 더 작다면 갔었다.
이번의 이동은... 제시된 정점이 나오면 무조건 이동해보고
값을 비교해야만 할것 같다..
한번 그대로 구현해보자.
아니다
두 정점을 각각 시작과 끝으로 하는 Dijkstra를 구하고,
시작점, 끝점을 그 이후에 연결하면 되겠다.
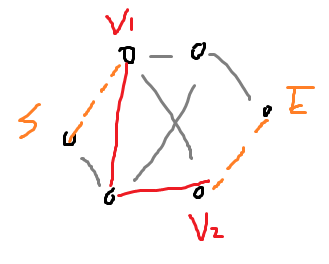
그렇다면 다익스트라를 총 3번해야한다는건데..
경로에 들어간 정점을 제외하고,
다익스트라를 함수로 구현해서 3번 호출하면 되겠다. 해보자.
시도
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <limits>
#include <set>
using namespace std;
int N, E;
vector<pair<int, int>> connection[801];
const int INF = numeric_limits<int>::max();
int d[801] = {0, };
set<int> visited; //전체 과정에서 사용된 정점
int track[801] = {0, }; //역추적배열
int Dijkstra(int, int);
bool zeroFlag = false;
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
int sum = 0;
// 입력
cin >> N >> E;
while(E--)
{
int a, b, c;
cin >> a >> b >> c;
connection[a].push_back({c, b});
}
int v1, v2;
cin >> v1 >> v2;
// D1
sum += Dijkstra(v1,v2);
// D2
if(v1 != 1)
{
sum += Dijkstra(1,v1);
}
// D3
if(v2 != N)
{
sum += Dijkstra(v2, N);
}
if(zeroFlag == true)
{
cout << -1;
return 0;
}
cout << sum;
return 0;
}
int Dijkstra(int start, int end)
{
cout << "DIDIDIDI";
memset(d, INF, sizeof(d));
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
d[start] = 0;
pq.push({d[start], start});
while(!pq.empty())
{
int cur_Dist = pq.top().first;
int cur_Index = pq.top().second;
pq.pop();
if(d[cur_Index] != cur_Dist)
{
continue;
}
for(auto next : connection[cur_Index])
{
int next_Dist = next.first;
int next_Index = next.second;
// 방문한 정점은 무시
if(visited.find(next_Index)==visited.end())
{
continue;
}
if(d[next_Index] <= next_Dist)
{
continue;
}
else
{
track[next_Index] = cur_Index;
d[next_Index] = next_Dist;
pq.push({d[next_Index], next_Index});
}
}
}
cout << "start : " << start << " /end : " << end << " /dist : "<< d[end] << "\n";
// 경로가 없을 경우
if(d[end] == INF)
{
zeroFlag = true;
return 0;
}
cout << "what i used : ";
visited.insert(start);
int index = end;
while(true)
{
visited.insert(index);
//cout << index << " ";
if(track[index] == start)
{
return d[end];
}
else
{
index = track[index];
}
}
cout << "\n";
return 0;
}출력이 아예 되지 않는다.
아마도 무한루프를 돌기 때문인 것 같은데..
왜 무한루프를 돌까..?

음..
혹시몰라서 제출해보니
시간초과가 났다.
무한루프 떄문이겠지..?
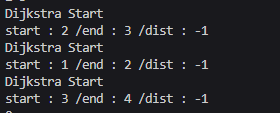
마지막의 visited추가부분을 주석처리하고 조금 수정해보니
d[end]가 이상하게 나온다.
왜?
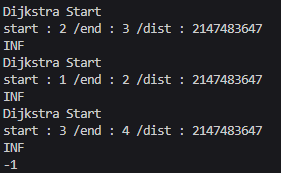
fill로 수정하니 INF가 채워지긴 했다.
추가로, visited에 저장해야할 것은 정점이 아니라 간선을 저장해야만 한다..
음...
밟은 간선을 또 밟을 수 있다는 조건을 무시했나?
간선으로 수정해도 되질 않는다.
간선을 중복해서 절대 밟지 않을거라 생각한 내 생각이 오류다.
음...
그렇다면 어떻게 해야할까..
4 5
1 2 100
1 3 1
2 3 1
2 4 10
3 4 1
1 2기본 반례에서도 아래처럼 이상한 값이 나온다..
1에서 2로가는 최소거리는 2여야만한다..
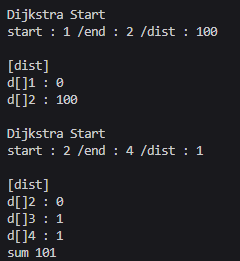
다익스트라 자체를 다시 정확히 구현해본다.
시도 2
아래의 2개를 신경썼다.
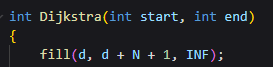
- fill을 통해 배열의 시작부터 끝까지 INF하였다.
memset을 통한 초기화를 하면 동작이 이상하게 된다.
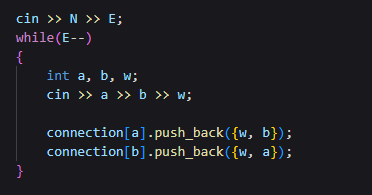
- 양방향 연결이기 떄문에 위처럼 진행해야했다.
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <limits>
#include <set>
using namespace std;
int N, E;
vector<pair<int, int>> connection[801];
const int INF = numeric_limits<int>::max();
int d[801] = {
0,
};
int track[801] = {
0,
}; // 역추적배열
int Dijkstra(int, int);
bool zeroFlag = false;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int sum = 0;
// 입력
cin >> N >> E;
while (E--)
{
int a, b, c;
cin >> a >> b >> c;
connection[a].push_back({c, b});
connection[b].push_back({c, a});
}
int v1, v2;
cin >> v1 >> v2;
// D1
sum += Dijkstra(v1, v2);
// D2
if (v1 != 1)
{
sum += Dijkstra(1, v1);
}
// D3
if (v2 != N)
{
sum += Dijkstra(v2, N);
}
if (zeroFlag == true)
{
cout << -1;
return 0;
}
cout << sum;
return 0;
}
int Dijkstra(int start, int end)
{
fill(d, d + N + 1, INF);
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
d[start] = 0;
pq.push({d[start], start});
while (!pq.empty())
{
int cur_Dist = pq.top().first;
int cur_Index = pq.top().second;
pq.pop();
if (d[cur_Index] != cur_Dist)
{
continue;
}
for (auto next : connection[cur_Index])
{
int next_Weight = next.first;
int next_Index = next.second;
if (d[next_Index] <= cur_Dist + next_Weight)
{
continue;
}
else
{
d[next_Index] = cur_Dist + next_Weight;
pq.push({d[next_Index], next_Index});
}
}
}
cout << "start : " << start << " /end : " << end << " /dist : " << d[end] << "\n";
return d[end];
}
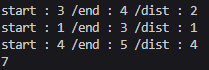
위같은 연결에서 오류가 발생했다.
그 이유는, 중복된 경로가 존재하기 때문이다. 1-4
흠...
어떻게 해결해야하지?
해결
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <limits>
#include <set>
using namespace std;
int N, E;
vector<pair<int, int>> connection[801];
const int INF = numeric_limits<int>::max();
int d[801] = {
0,
};
int track[801] = {
0,
}; // 역추적배열
int Dijkstra(int, int);
bool zeroFlag = false;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int sum1 = 0; // 1-v1-v2-N
int sum2 = 0; // 1-v2-v1-N
// 입력
cin >> N >> E;
while (E--)
{
int a, b, c;
cin >> a >> b >> c;
connection[a].push_back({c, b}); //* 양방향 연결임을 간과했었다
connection[b].push_back({c, a});
}
int v1, v2;
cin >> v1 >> v2;
// 순방향 1-v1-v2-N
sum1 += Dijkstra(v1, v2);
sum1 += Dijkstra(1, v1);
sum1 += Dijkstra(v2, N);
// 꼰방향 1-v2-v1-N
sum2 += Dijkstra(v1, v2);
sum2 += Dijkstra(1, v2);
sum2 += Dijkstra(v1, N);
// 예외처리
if (zeroFlag == true)
{
cout << -1;
return 0;
}
// 더 작은 경로값 출력
if (sum1 <= sum2)
{
cout << sum1;
}
else
{
cout << sum2;
}
return 0;
}
int Dijkstra(int start, int end)
{
if (start == end)
{
return 0;
}
// zeroFlag 넣으면 더 할필요 없으므로 시간단축
if (zeroFlag == true)
{
cout << -1;
return 0;
}
fill(d, d + N + 1, INF); //* memset이 아니라 fill을 사용해야만 했다.
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
d[start] = 0;
pq.push({d[start], start});
while (!pq.empty())
{
int cur_Dist = pq.top().first;
int cur_Index = pq.top().second;
pq.pop();
if (d[cur_Index] != cur_Dist)
{
continue;
}
for (auto next : connection[cur_Index])
{
int next_Weight = next.first;
int next_Index = next.second;
if (d[next_Index] <= cur_Dist + next_Weight)
{
continue;
}
else
{
d[next_Index] = cur_Dist + next_Weight;
pq.push({d[next_Index], next_Index});
}
}
}
//cout << "start : " << start << " /end : " << end << " /dist : " << d[end] << "\n";
// 도착점까지 거리가 INF라는것은, 한번도 방문하지 못했기 떄문
if (d[end] == INF)
{
zeroFlag = true;
}
return d[end];
}
풀이
문제가 되었던 반례를 해결하기 위해,
Dijkstra 1세트를 하나 더 추가했다.
그리고 값을 비교하여 더 작은 값을 출력했다.
다익스트라 알고리즘이 어려웠다기보다,
해당 알고리즘을 사용은 하는데,
조건에 맞게 예외처리하는 것과 반례들이 예상하기 어려웠다.
다익스트라를 딱히 개조하지는 않았고,
블랙박스 모듈처럼 사용했다는것에 문제자체 어렵지는 않다고 생각한다.
하지만 시간은 엄청 걸렸다.