우선 문제 전에, 벨만포드와 플로이드워셜 중에
플로이드워셜 하나만 배우려고 한다.
위의 백준 문제의 수로 일단 플로이드-워셜이 범용성이 더 높다고 판단했고,
실제 문제들을 보았을 때, 벨만포드는 평균 플레-다이아 수준이었고,
플로이드-워셜은 골드 수준이어서 플로이드 워셜로 정한다.
https://www.acmicpc.net/workbook/view/3581
다익스트라로 도움을 정확하게 받아서,
플로이드 알고리즘에도 해당 강의를 참고하려고 한다.
3. 11404 - FLO-WAR
https://www.acmicpc.net/problem/11404
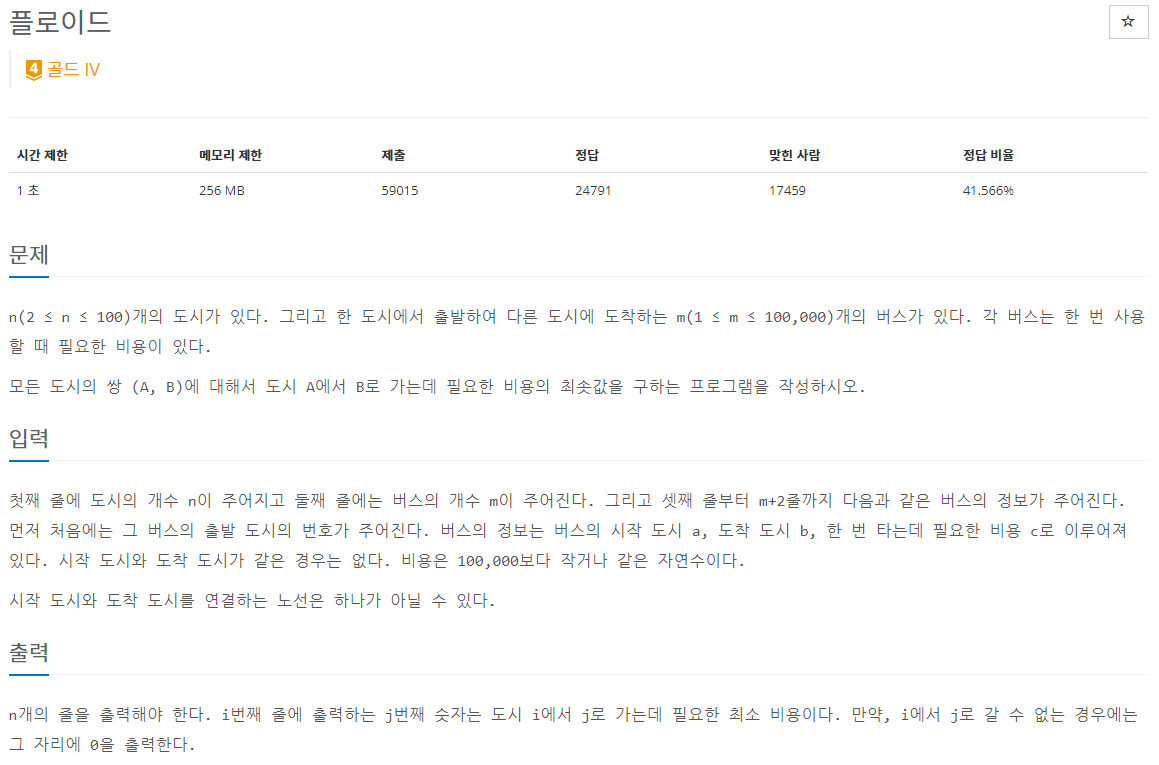
플로이드 알고리즘의 정석인 문제.
다익스트라보다 구현이 쉽다고 한다.
구현해본다.
해결
#include <iostream>
using namespace std;
//const int INF = numeric_limits<int>::max();
const int INF = 100000000;
int d[101][101];
int N, M;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> N >> M;
// INF로 다 채워둠
for (int i = 1; i <= N; i++)
{
fill(d[i], d[i] + N + 1, INF);
}
// 연결 입력을 받아서 d에 바로 저장
while (M--)
{
int a, b, w;
cin >> a >> b >> w;
d[a][b] = min(d[a][b], w); // 시작/도착 도시를 연결하는 노선은 하나가 아닐 수 있다.
}
// 본인과의 거리는 0으로 설정
for (int i = 1; i <= N; i++)
{
d[i][i] = 0;
}
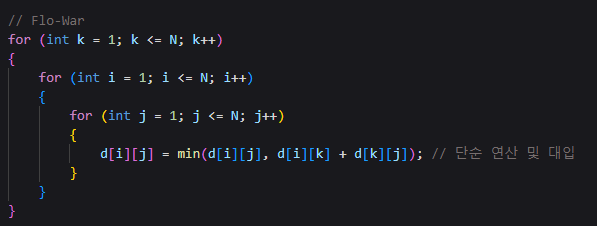
// Flo-War
for (int k = 1; k <= N; k++)
{
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
// 출력
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
if (d[i][j] == INF)
{
cout << "0 ";
}
else
{
cout << d[i][j] << " ";
}
}
cout << "\n";
}
return 0;
}풀이
[Flo-War 알고리즘으로 문제를 풀 때 유의해야 할 것들]
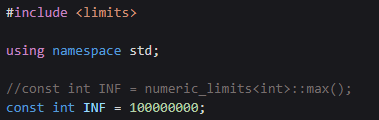
-
Dijkstra알고리즘에서는 INF를 int의 최대값으로 두었는데,
여기서는 그렇게 하면 안된다.
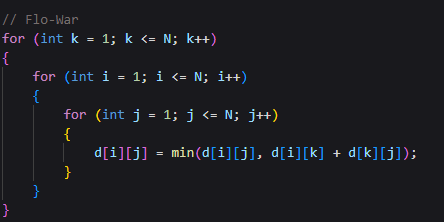
-
그 이유는, Flo-War알고리즘에서
d[][]값이 뭐든간에, 더하기 때문이다.
그래서 해당 부분에 조건을 걸어 INF면 더하지 못하게 막으면 되긴하나,
적당히 큰 수인 1억을 넣으면 쉽게 해결된다고 한다.
참고할것 -
그리고 위의 부분에서 min으로 최소값을 비교하는데,
해당 부분이 시간을 많이 잡아먹는다고 한다.
min이라는 함수에 대입을 계속 해야하므로,
그냥 if문을 사용하여, 더 작다면 더 작은값을 d[i][j]에 대입하는 것으로
시간을 30%정도 아낄 수 있다고 한다. -
https://www.acmicpc.net/board/view/55142
보통 1초에 2억개의 연산을 할 수 있다고 생각하면 되지만,
간단한 연산이라면 20억개도 가능은 하다라는 내용이다.
그 예시가 지금 문제이다.
예시로 준 정점의 개수가 1000개이다.
Flo-War 알고리즘으로 푼다면, for문을 3번 돌아야만하고,
10억개의 연산이 진행된다.
간선의 개수는 관계없다
따라서 1초안에 통과하지 못하는게 맞지만,
Flo-War알고리즘이 for문을 3번 도는 동안의 연산이 매우 간단해서 통과하는 문제이다.
이전 내용에서처럼 if문을 사용하여 min을 더 경량화할 수 있다
4. 11780 - FLO-WAR
https://www.acmicpc.net/problem/11780
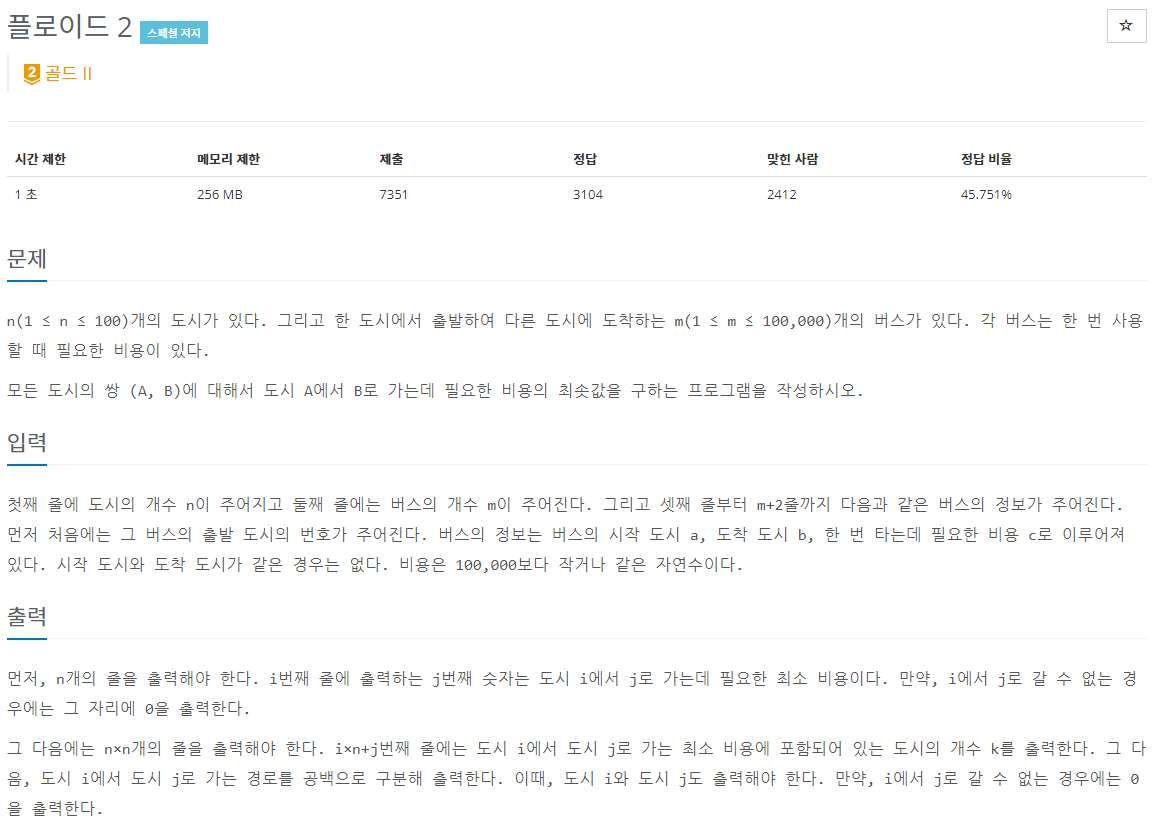
플로이드1의 변형문제이다.
기존 2차원배열 d를 출력하여
모든 정점간의 최소거리를 출력하는건 1과 같다.
그리고 추가로,
해당 최소거리가 나오기까지 몇개를 거쳤는지, 어느 정점을 거쳤는지를 쭉 나열해야한다.
Flo-War로 경로탐색을 해야한다는 말인데..
어떻게 할까?
방법은 2차원 배열을 하나 더 만드는 것이라고 한다.
해결
#include <iostream>
#include <vector>
using namespace std;
int N, M;
int d[101][101];
int passIdx[101][101];
const int INF = 100000000;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> N >> M;
// 1 INF
for (int i = 1; i <= N; i++)
{
fill(d[i], d[i] + N + 1, INF);
}
// 2 입력
while (M--)
{
int a, b, w;
cin >> a >> b >> w;
d[a][b] = min(d[a][b], w); // min 해줘야함
passIdx[a][b] = b;
}
// 3 본인
for (int i = 1; i <= N; i++)
{
d[i][i] = 0;
}
// 4 Flo-War
for (int k = 1; k <= N; k++)
{
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
// i~j로 가는 것보다 k를 거쳐서 가는 것이 빠르다면,
if(d[i][j] > d[i][k] + d[k][j])
{
d[i][j] = d[i][k] + d[k][j]; // d를 갱신
passIdx[i][j] = passIdx[i][k]; // maxIdx를 갱신
}
// 따라서 i에서 j로 가는 최단경로는 i에서 k를 지나온 정점을 무조건 포함한다.
}
}
}
// 5 출력
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
if (d[i][j] == INF)
{
cout << 0 << " ";
}
else
{
cout << d[i][j] << " ";
}
}
cout << "\n";
}
// 5-2 출력 2
for(int i=1;i<=N;i++)
{
for(int j=1;j<=N;j++)
{
if(d[i][j] == 0 || d[i][j] == INF) //최단경로를 표시할 수 없는 경우
{
cout << "0 \n";
continue;
}
vector<int> path;
int idx = i; // i를 시작점으로 두고, j로 가는 경로를 구한다.
while(idx != j)
{
path.push_back(idx); // 지나온 정점을 역추적하여 vector에 담는다
idx = passIdx[idx][j];
}
path.push_back(j); // 종료점을 마지막으로 담는다.
cout << path.size() << " ";
for(auto x : path)
{
cout << x << " ";
}
cout << "\n";
}
}
}풀이
https://www.youtube.com/watch?v=dDDy2bEZRA8&list=PLtqbFd2VIQv4O6D6l9HcD732hdrnYb6CY&index=29
정확히 passIdx[][]의 동작원리를 잘 모르겠다..
음..
역추적하고 출력하는 과정은 알겠는데,
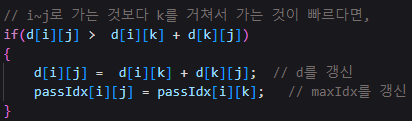
왜 passIdx[i][j]를 한 것이 passIdx[i][k]가 되어야하는지 모르겠다..
이것만 이해하면 되는데.. 흠..
포함해야만 최단경로가 되는 점을 passIdx[][]라고 정의했다는 걸 명심해야한다.
그래서 d[i][j]로 가는 길에 k를 거치는게 더 빠르다면,
d를 k를 거치도록 갱신하고,
k를 거쳐야만 한다고 적어넣는 것이다.
그러니까 거쳐야지만 가장 빠른 그 최단거리와,
그 최단거리를 가능하게 하는 점의 인덱스가 들어간 것이다.

위의 부분은 그 점들을 추적하는 코드이다.
이중for문 ij 안에 들어있는 코드이고, i부터 j로 가는 경로를 추적한다.
만약에 1 4 라고 한다면,
먼저 idx=1이되고, vector에 idx가 push된다.
그리고 passIdx[1][4]를 idx로 둔다.
그러면 1에서 4로 갈 때 반드시 거쳐야 최단거리가 되는 점이 기록되어있을 것이고,
해당 점이 idx가 된다.
그러면 해당 점으로부터 passIdx[idx][j]를 또 구하는 것이고,
쭉쭉 가다가 결국 idx가 j인, 목적지가 idx가 되는 상황이 올 것이다.
그러면 종료.
참고로 passIdx[i][i]부분은 값이 갱신되지 않는다. 쓰레기 값이 들어가있다.




유익한 글이었습니다.