1. 1520 - DFS / DP
https://www.acmicpc.net/problem/1520
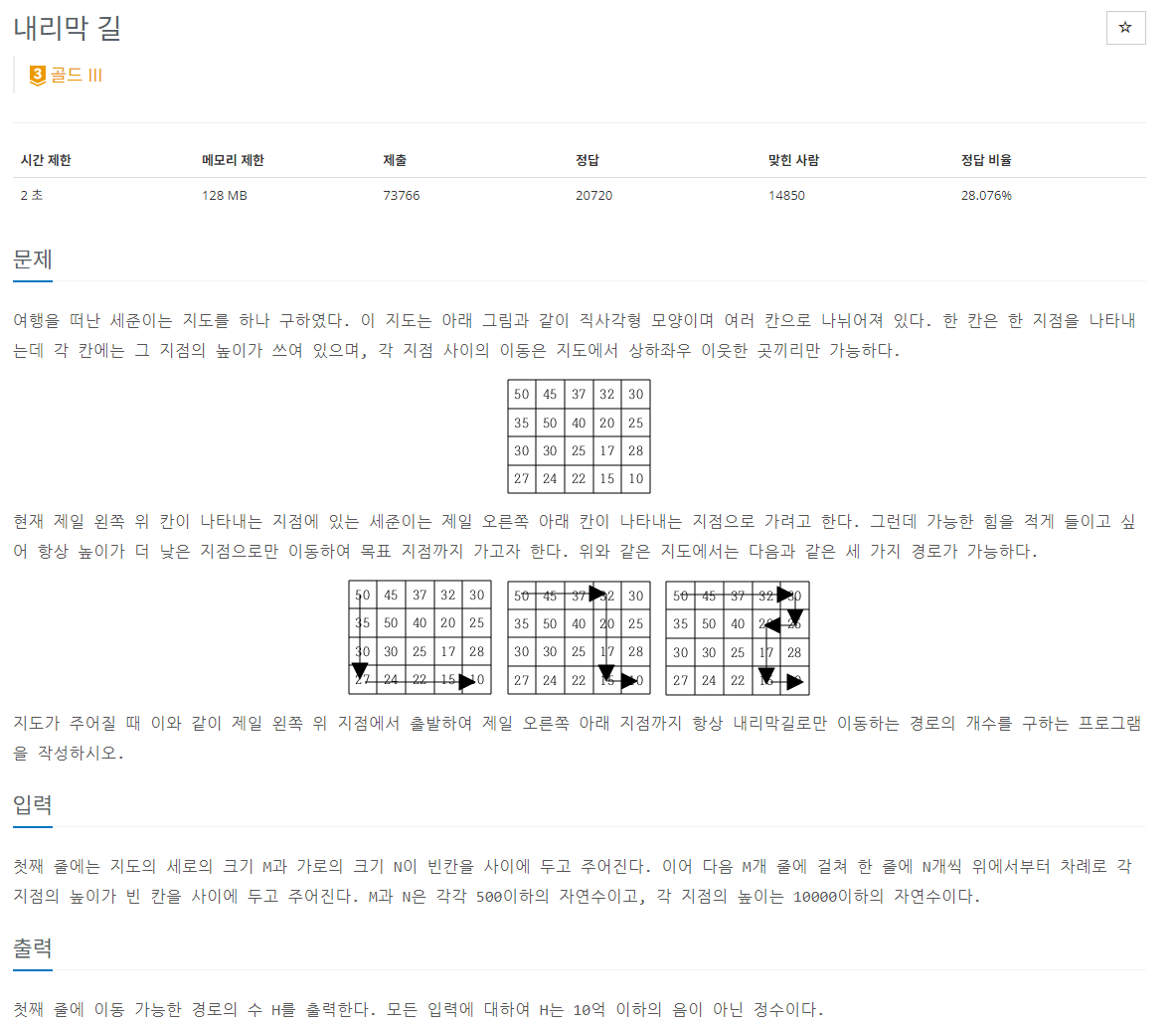
DFS로 풀어야 할 것 같다는 생각이 들었다.
DP문제라고 보았는데, DP를 왜 쓸까 생각도 들었다.
그냥 목표점에 도달하면 count를 세고,
출력만 하면 되는게 아닌가??
일단 해본다.
시도
#include <iostream>
using namespace std;
int cx[4] = {1, 0, -1, 0};
int cy[4] = {0, -1, 0, 1};
void DFS(int, int);
int map[501][501];
int M, N;
int count = 0;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> N >> M; // 세로 가로 - 가로 세로로 쓸 예정
/* 0으로 초기화
for (int i = 0; i < N; i++)
{
fill(&map, &map+500, 0);
}
*/
// 입력
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
cin >> map[i][j];
}
}
DFS(0, 0);
cout << count;
return 0;
}
void DFS(int x, int y)
{
if (x == N - 1 && y == M - 1)
{
count++;
}
for (int i = 0; i < 4; i++)
{
int dx = x + cx[i];
int dy = y + cy[i];
if (dx < 0 || dy < 0 || N < dx || M < dy)
{
continue;
}
else
{
if (map[dx][dy] < map[x][y]) // 내리막길이라면
{
DFS(dx, dy);
}
}
}
}DFS로 구현했는데.. 음
시간초과가 났다.
역시 카테고리에 맞게 DP를 사용해야만 하는건가
사용한다면 어떻게?
특정 좌표를 방문할 때마다 map크기의 dp에 표시를 해야하나?
표시를 한다고 뭐가 달라지나? 오히려 그냥 도착하면
count 변수 하나만 증가시키는게 효율적인 것 같은데?
갔던 DFS경로를 탐색하지 않도록 막는 방식으로
DFS횟수를 제한하도록 DP를 작성해야만 의미가 있는 것 같은데..
음.. 어떻게..?
어떻게 탐색하지 않고도 목적지가 아닌걸 알고 막을까?
가장 첫 DFS 경로를 구해버리고
그 다음 DFS가
해당 경로 내에 존재하는 좌표중 하나라도 갔다면 무조건
도착지까지 갈 수 있으므로 생략하는 방식을 쓸까?
시도 2
#include <iostream>
#include <vector>
using namespace std;
int cx[4] = {1, 0, -1, 0};
int cy[4] = {0, -1, 0, 1};
int DFS(int, int);
int map[501][501];
int d[501][501]; // DP
int M, N;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> N >> M;
// 입력
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
cin >> map[i][j];
d[i][j] = -1; // d -1로 초기화
}
}
cout << DFS(0, 0);
return 0;
}
// 목적지가 아니라면 최종적으로 d[x][y]를 반환한다.
int DFS(int x, int y)
{
if (x == N - 1 && y == M - 1)
{
return 1;
}
if (d[x][y] == -1) // 한번도 방문한 적이 없다면,
{
d[x][y] = 0; // 방문 표시를 한다
for (int i = 0; i < 4; i++)
{
int dx = x + cx[i];
int dy = y + cy[i];
if (dx < 0 || dy < 0 || N <= dx || M <= dy)
{
continue;
}
else
{
if (map[dx][dy] < map[x][y]) // 내리막길이라면
{
d[x][y] += DFS(dx, dy); // d(dxdy)값을 d(xy)에 더함
}
}
}
}
return d[x][y];
}풀이
다른 풀이를 참고하였다
방문한 점을 기록하지 말고,
도착했다면, 도착한 점을 d[x][y] = 1이라는 값으로 두고,
이전 d 좌표에서 해당 값을 반환받고 더하도록 하였다.
즉, 해당 좌표에서 갈 수 있는 경우의 수가 d로 정해지고,
이 경우의 수를 역추적하여 시작노드까지 가져오게 되는 것이다.
DFS구현은 굉장히 쉬웠고, 답이 바로 나왔지만,
DFS속에서 중간 값을 저장해 놓는 방식을 생각하기 어려웠고,
DP의 3요소가 저장할공간/점화식/점화값 이라고 생각하는데,
주어진 틀에서 이 점화식을 생각하고 적용하기가
꽤 어렵다고 느껴졌다.
하지만 DP를 사용하므로써,
큰 카테고리의 문제의 부수적으로 사용하며 시간을 줄일 수 있었다.
2. 11066 - DP
https://www.acmicpc.net/problem/11066
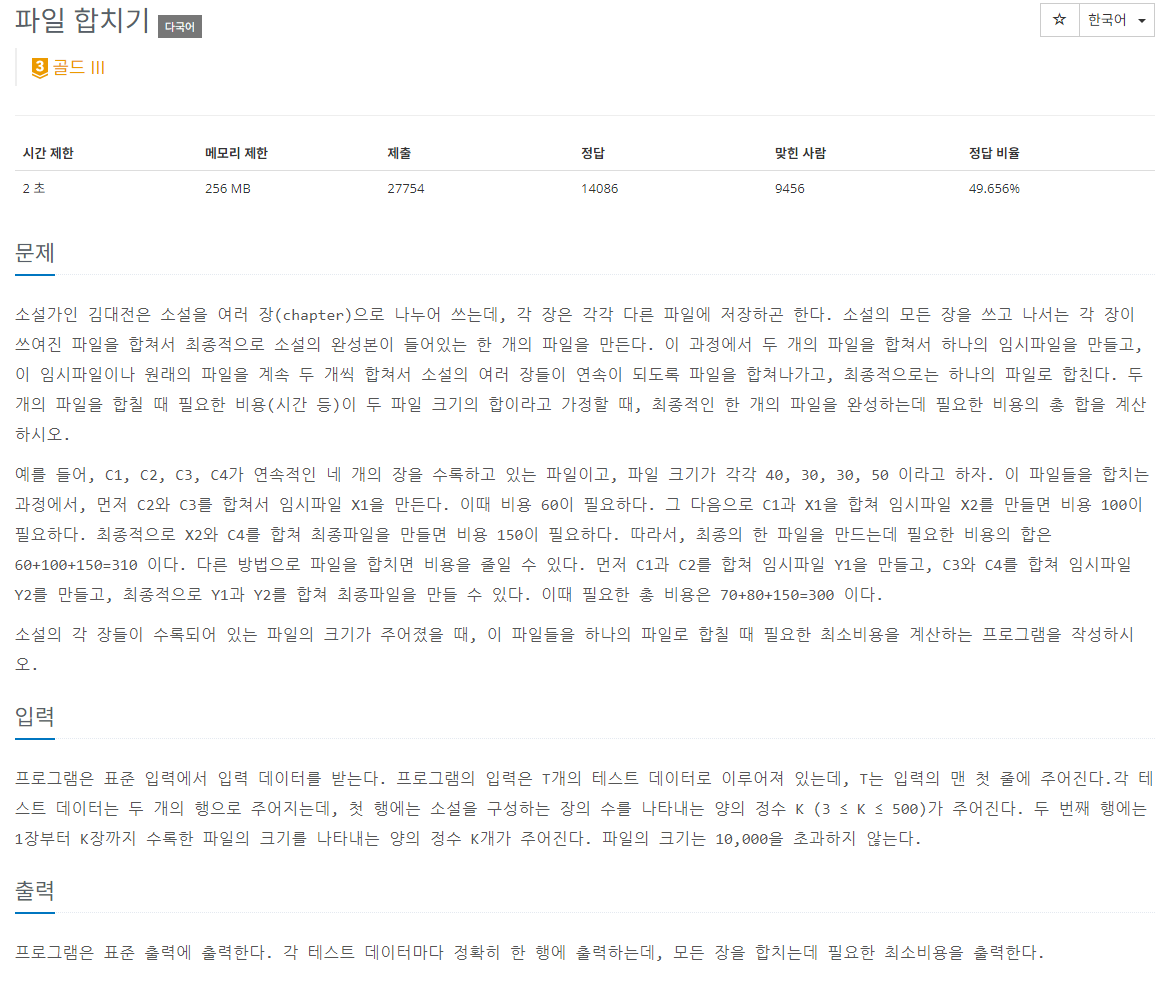
파일 크기가 주어졌을 때, 합치는 최소값을 구하는 문제이다.
총 합은 같다고 생각했지만, 아니다. 더하는 비용이 존재한다.
40 30 70인 경우에, 어떻게 합치든 140같지만,
40+30을 하는 것의 비용은 70이다.
그리고 70+70하는 것의 비용은 140이다.
그렇다면, 70+140을 하는게 총 비용의 값으로 보는 것이다.
(1+2) + (1+2+3)
연산의 값들의 합이 최종 비용인 것이다.
음.. 어떻게 DP를 구현할까
우선 이전값이 다음에 쓰이는 경우는,
두 파일만 더할 수 있으므로, 각 2개의 파일씩의 합을 미리 구하는게 나아보이고,,
그 값을 어떻게 쓸까..
3차원 배열?
d[인덱스1][인덱스2][단계]
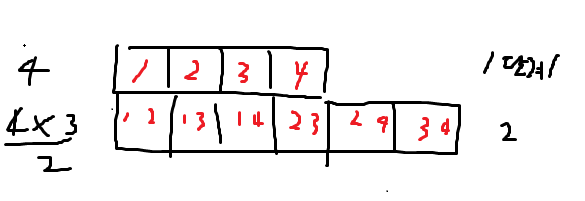
이런식으로 단계를 나눠서
모든 값들을 미리 계산하려고 했는데,
생각해보니 최대값인 500을 넣는다면,
기하급수적으로 단계마다 구해야하는 값들이 증가할 것이라고 생각했다.
n! 만큼 증가할 것 같아서 이 구현법은 일단 스킵한다.
그렇다면 어떤 방법을 써야하지?
음... 그냥 구현법을 사용해야할 것 같은디..
음.. 일단 이전의 합의 모든 경우를 다 계산해 두어야만 하는건 필수라고 생각한다.
다만 그 합들을 새로운 변수에 계속 넣는다면,
그 크기가 어마어마해질 것이다.
흠..
와 정말 모르겠다..
구현법이 생각이 나질 않는다..
한 문제에 2일동안 매몰된 것 같은데..
일단 스킵하려고 한다....
처음으로 포기선언
https://melonicedlatte.com/algorithm/2018/03/22/051337.html
