위의 내용대로 공부해본다.
그리고
나의 전형적인 구현방식을 정의하고,
각 방식끼리의 차이점을 정리한다.
그리고 각각 최단 경로의 경로 자체를 출력하는 방식도 살펴본다.
1. 최단경로 알고리즘
1-0. BFS / DFS
- BFS는 가중치가 없는 경우여야만 가능하다. 큐에 들어가는 순서가 중요하기 때문.
- 아니면 가중치를 작은 것부터 우선으로 돌면 된다. (이게 다익스트라의 기원)
- DFS로는 모든 값을 다 구하고 최단경로인지 계산하면 될 것이다.
하지만 O(V!)의 시간이 걸릴 수 있다.
따라서 입력값이 작은 경우에 사용 가능하고,
제약조건을 적절히 설정해야만 한다.
1-1. 다익스트라 O(ElgV)
https://www.acmicpc.net/problem/1753
양수 / BFS + priority_queue / 한점-다른점
A.설명
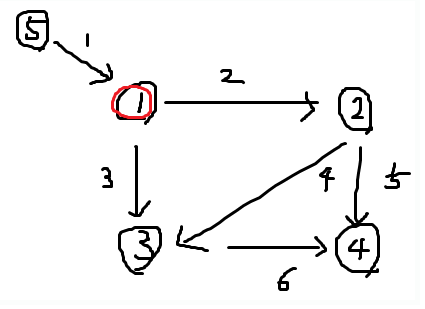
- 다익스트라는 한 시작점으로부터 다른 점까지의 최단 거리를 구하는 것이다.
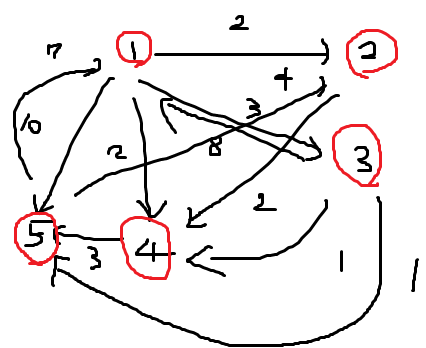
(아래의 그림의 경우라면, 1->1 / 1->2 / 1->3 / 1->4 / 1->5) - 단방향/양방향에 상관없다. 양방향이면 연결을 추가해주면 되므로.
- BFS + priority_queue를 사용하고,
BFS에 의해 가장 먼저 목적지에 도착하더라도,
다른 목적지에서 갈 수 있는 연결도 있다면,
그리고 그게 최소값이 된다면, 갱신해나간다. - priority_queue는 단순히 현재 갈 수 있는 가장 짧은 간선을 의미하고,
현재 가장 짧은 간선을 통해서 목적지를 처음 도착했을 때의 값이
무조건 정답은 아니기 때문에 BFS를 조금 수정하여 사용하는 것이다.
ex) A->C를 구하기 위해
A->B가 1, B->C가 4라서 5가 걸렸을 때,
A->D가 3, D->C가 1이면, 4가 된다.
따라서 현재 가장 짧은 간선만 따라가는 것은 무조건 최적해가 아니다. - 음수 가중치가 있는 경우는 수행 불가
- 한 시작점에서만 시작하므로, 모든 정점간 최단거리를 구하지는 않는다.
(for문을 돌려 모든 시작점에서 돌리면 간단히 해결됨)
(하지만 효율적이지는 않다)
B. 전형적인 구현 방식
자료구조
1. 연결을 담을 connection 배열
vector<pair<int, int>> connection[N]
(통일성을 위헤 앞은 가중치, 뒤는 정점 인덱스를 담는다)
2. 최단 거리를 담을 d 배열
int d[N]d[5]라면, 점 5까지 가는 최단 거리를 의미.
3. 다익스트라의 핵심인 priority_queue
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
구현법
1. 987654321로 d배열 초기화
(문제의 조건에 따라 달라짐. E * 가중치의 최대값 보다 커야 함)
2. BFS처럼 시작점의 거리d[Start]=0으로 두고,
priority_queue에 넣음pq.push({d[Start], Start})
3. BFS문 진행
- 현재 큐에서 뽑은 가중치가, 현재 d의 최단거리와 다르다면,
현재 큐로는 최단거리를 만들 수 없으므로 스킵.
(항상 큐에서 뽑은 가중치 >= d 이다)- 연결된 간선을 순회하며, 계산 값이 더 작다면 갱신하고 큐에 넣는다.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int V, E, St;
vector<pair<int, int>> connection[20001]; // 1입력 수가 많아서 vector로 표현
int d[20001]; // 2최단 거리
int track[20001];
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin >> V >> E >> St;
for(int i=0;i<E;i++)
{
int u, v, w;
cin >> u >> v >> w;
connection[u].push_back({w,v});
}
// 모든 최단거리를 일단 987654321로 초기화
// 해당 값은 범위가 중요한데, E * 가중치 최대값을 초과하는 값으로 설정
for(int i=0; i<=V; i++)
{
d[i] = 987654321;
}
// 3priority_queue
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
// 가중치가 0이기 때문에 St라는 시작점에서 가장 먼저 시작하게 된다.
d[St] = 0;
pq.push({d[St], St});
// [BFS 방식과의 차이점]
// 1 일반 queue가 아니라 오름차순 정렬하는 priority_queue에 push
while(!pq.empty())
{
int w = pq.top().first;
int v = pq.top().second;
pq.pop();
// 새로운 경로가 더 커서 굳이 갱신할 필요 없다면 스킵.
if(d[v] != w)
{
continue;
}
// 현재 점에 연결된 간선을 순회
for(auto next : connection[v])
{
// 새로운 경로로 갱신할 수 없다면, 스킵.
if(d[v]+next.first < d[next.second])
{
d[next.second] = d[v]+next.first;
track[next.second] = v; // 여기서 갱신
pq.push({d[next.second], next.second});
}
}
}
// 출력부
for (int i = 1; i <= V; i++)
{
if (d[i] == 987654321)
{
cout << "INF\n";
}
else
{
cout << d[i] << "\n";
}
}
// 출력부 2
cout << "Track\n";
for (int i = 1; i <= V; i++)
{
if (track[i] == 0)
{
cout << i << "\n";
}
else
{
cout << track[i] << "\n";
}
}
return 0;
}C. 경로 찾기
- track이라는 1차원 배열을 하나 생성한다.
- track[1]이라면, 1을 가기 위한 최단거리의 바로 전의 점
- 갱신되는 시점에서 해당 track배열을 갱신한다.
// 갱신할 수 있다면, 갱신하고, priority_queue에 push.
else
{
d[next.second] = d[v] + next.first;
track[next.second] = v; // 여기서 갱신
pq.push({d[next.second],next.second});
}
// 출력부 2
cout << "Track\n";
for (int i = 1; i <= V; i++)
{
if (track[i] == 0)
{
cout << i << "\n";
}
else
{
cout << track[i] << "\n";
}
}
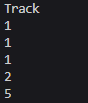
1부터 시작하는데 1의 전은 없으므로 1,
2는 1, 3은 1
4는 2거쳐서 오므로 2
5도 전이 없으므로 5로 출력되게 만들었다.
D. 사이클이 있는지 확인
- 사이클이 있는 경우에 애초에 사용하지 않음
1-2. 벨만포드 O(EV)
https://www.acmicpc.net/problem/11657
음수 / 사이클은 탐지만 가능 / 한점-다른점 / 다익스트라보다 무거움
- 변형하면 사이클이 존재해도 가능 <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
- 정말 이해가 안 돼서 찾아본 글
https://yabmoons.tistory.com/365
A.설명
- 벨판포드도 한 시작점으로부터 다른 점까지의 최단 거리를 구하는 것이다.
- 단방향/양방향 상관 없지만, 벨만포드는 음수 가중치도 허용한다.
따라서 음수의 사이클이 있다면 문제가 발생. - 아래의 과정을 V-1번 반복한다.
- 매번 전체 간선을 순환하는데, 비용이 더 작다면 최단거리 테이블을 갱신
- 음수 사이클이 발생했는지 확인하고 싶다면,
1번 더 반복한 V번째에 갱신이 일어난다면 음수 사이클이 존재.
그 이유는 V-1번째에 모든 정점의 최소비용이 정의되는 것이 증명되었기 때문. - 다익스트라는 지금 당장 눈앞에 보이는,
방문하지 않은 점에 대해서 가장 최소비용의 간선을 따라
Greedy하게 갔지만, - 벨만포드는 방문했더라도 매번 모든 간선을 확인한다.
즉, 다익스트라는 벨만포드의 한 경우의 수에 포함되는 개념.
(양수만 있을 경우, 그 경우가 최적해가 되는 것)
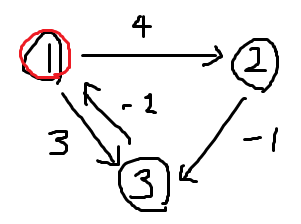
내가 생각할 때에는 위의 그래프는 다익스트라로도 풀 수 있을 것 같다.
그 이유는 아무리 음수 사이클이더라도 무한히 음수가 되는 사이클이 없기 때문.
B. 전형적인 구현 방식
자료구조
1. 연결을 담을 connection 배열
vector<pair<int, pair<int, int>>> connection
시작점, {끝, 가중치} 를 의미
2. 최단 거리를 담을 d배열
long long d[N]
문제마다 int나 long long을 붙여서 사용.
(웬만하면 long long 사용하자)
3. (음수) 사이클이 있는지 판단할 플래그 변수
bool isCycle = false
구현법
1. INF를 직접 정의하여 d배열 초기화
#define INF 1e9
e9는 10의 9승을 의미, 따라서 1e9는 10억
int의 최대값이 21억이므로 2e9를 사용하기도 한다.
2. 시작점의 거리d[Start] = 0으로만 두고 벨만포드 실행
3. 벨만포드 진행
- V번 반복 (해당 인덱스가 쓰이는 일 없고, 단순 반복문)
- 모든 간선을 순회
- 간선의 from의 d값이 INF라면, continue
(중요한 부분. 해당 부분이 없으면 동작하지 않는다)d[from]+cost < d[to]갱신해야하면 갱신.
- 만약 갱신시에 V번째 반복이라면,
사이클이 존재하므로isCycle = true
#include <iostream>
#include <vector>
#include <queue>
#define INF 1e9
using namespace std;
int V, E;
//vector<pair<int, int>> connection[501];
vector<pair<int, pair<int, int>>> connection; // 시작점, {끝, 가중치}
long long d[501];
bool isCycle = false;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> V >> E;
for (int i = 0; i < E; i++)
{
int u, v, w;
cin >> u >> v >> w;
// 시작점, {끝, 가중치}
connection.push_back({u,{v,w}});
}
// 모든 노드의 최소값을 일단 987654321로 초기화
for (int i = 0; i <= V; i++)
{
d[i] = INF;
}
// 시작은 0으로 둔다.
// 시작점은 여기서 설정하게 된다.
d[1] = 0;
// i는 정점의 개수 V번 반복, V-1번째에 최단 거리가 정해지지만,
// 마지막 V번째 작업을 통해 사이클을 확인
for(int i=1; i<=V; i++)
{
// 모든 간선을 순회한다.
for(int k=0; k<E; k++)
{
int from = connection[k].first;
int to = connection[k].second.first;
int cost = connection[k].second.second;
// 해당 코드가 없으면 안됨
// 방문한 적이 없는 정점에서 출발하는 간선은 무시해야 함.
if(d[from] == INF)
{
continue;
}
// 갱신할 수 있으면 갱신
if(d[from]+cost < d[to])
{
d[to] = d[from]+cost;
// 갱신을 하긴 했는데, V번째에 갱신되었다면, 음수 사이클 존재.
if(i==V)
{
isCycle = true;
}
}
}
}
// 출력부
if (isCycle)
{
cout << -1;
return 0;
}
else
{
// 문제는 1이 시작점이라서, 2부터 출력
// 2가 시작점이라면 1부터 출력하고, i==2인 경우를 생략하면 됨.
for(int i=2;i<=V;i++)
{
cout << (d[i] != INF ? d[i] : -1) << "\n";
}
}
return 0;
}
/* for문을 3개 사용하는 버전.. vector 배열 말고
벡터 하나에 모두 넣으면 되므로 사용하지 않는다.
// 이전 자료구조
connection[u].push_back({w, v});
for(int n=1; n<=V; n++)
{
// 정점 i의 j번째 연결
for(int i=1;i<=V;i++)
{
for(int j=0;j<connection[i].size();j++)
{
int w = connection[i][j].first;
int v = connection[i][j].second;
if(d[i]+w < d[v])
{
d[v] = d[i] + w;
if(n==V)
{
isCycle = true;
}
}
}
}
}
*/C. 경로 찾기
- 다익스트라와 똑같이 하면 된다.
- track이라는 1차원 배열을 하나 생성한다.
track[1]이라면, 1을 가기 위한 최단거리의 바로 전의 점
갱신되는 시점에서 해당 track배열을 갱신한다.
D. 사이클이 있는지 확인
- isCycle로 확인
- V-1 시점에서 최단거리가 모두 정해짐.
따라서 V번째에서 갱신된다면 (음수) 사이클이 존재.
(양수 사이클이라는 말도 이상하다.
최소거리니까 당연히 양수 사이클은 모양만 사이클이지
전혀 문제되지 않는다.)
1-3. 플로이드워셜 O(V^3)
https://www.acmicpc.net/problem/11404
음수 / 사이클이 있어도 가능 / 모든 한점-다른점
A.설명
- 한 개의 시작점이 아닌, 모든 정점간의 최단 거리를 구함.
- 벨만포드를 각 정점에 대해 돌려도 상관없지만
플로이드가 더 간단, 빠름, 사이클이 있어도 가능.
(벨만포드보다 더 빠른 이유는, for문이 3개임에도,
for문 내부의 코드가 상당히 간단하기 때문이다)
시간복잡도가 직접적인 수행시간을 의미하지는 않는다. 혼란주의 - 아래의 코드가 끝인 알고리즘이다.
d[i][j] = min(d[i][j], d[i][k] + d[k][j]) - 모든 점 k를 거쳐가며, 해당 길이 더 빠르면 거쳐가는 값으로 설정한다.
B. 전형적인 구현 방식
자료구조
1. 최단 거리를 담을 2차원 d배열
int d[101][101]
벡터가 아니고 그냥 배열이어야 하는 이유는,
간선의 시작과 끝을 명확히 인덱스로 표시할 수 있어야 하기 때문.
- 대신 connection 배열을 생성하지 않는다.
구현법
1. INF를 직접 정의하여 2차원 d배열 초기화
2. 각 점의 본인과의 거리는 0으로 설정
3. 플로이드 진행
- for문 3번 (kij)
- 아래 코드 실행. 끝.
d[i][j] = min(d[i][j], d[i][k] + d[k][j])
#include <iostream>
#define INF 1e9
using namespace std;
int V, E;
int d[101][101];
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin >> V >> E;
// 1 일단 INF로 모든 값을 채움
for(int i=1; i<=V; i++)
{
for(int j=1; j<=V; j++)
{
d[i][j] = INF;
}
}
// 2 입력 받아서 바로 d에 저장
for(int i=1; i<=E; i++)
{
int u, v, w;
cin >> u >> v >> w;
//d[u][v] = w; // 1 일반적인 경우
d[u][v] = min(d[u][v], w); // 2 현재 문제의 조건에 따름 - 두 점 잇는 간선은 여러개
}
// 3 본인과의 거리는 0으로 설정
for(int i=1; i<=V; i++)
{
d[i][i] = 0;
}
// 4 Floyd
for(int k=1; k<=V; k++)
{
for(int i=1;i<=V;i++)
{
for(int j=1;j<=V;j++)
{
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
// 출력
for(int i=1; i<=V; i++)
{
for(int j=1; j<=V; j++)
{
if (d[i][j] == INF)
{
cout << "0 ";
}
else
{
cout << d[i][j] << " ";
}
}
cout << "\n";
}
return 0;
}C. 경로 찾기
생략.. 3차원 배열을 만들어야 할 것 같다.
아래의 방법으로는 구해지지 않는다.
그리고 구하는 사람도 문제도 찾지 못했다..ㅇ
int track[101][101]- 입력을 받을 때, track으로 이전의 값이 뭔지 미리 설정해둔다.
if(d[u][v] > w)
{
d[u][v] = w;
track[u][v] = u;
}track[u][v]라는 것은, u를 시작점으로 보았을 때,
v의 이전 노드를 의미.
- 그리고 최단거리를 갱신할 때, track 값도 갱신.
if(d[i][j] > d[i][k] + d[k][j])
{
d[i][j] = d[i][k] + d[k][j];
track[i][j] = k;
track[i][k] = i;
}
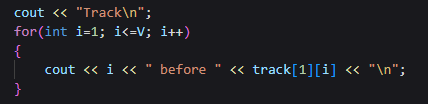
간단하게 track[1][i]로 1에 대한 경로만 출력해 보았다.
Track - 1
1 before 0
2 before 1
3 before 1
4 before 1
5 before 3D. 사이클이 있는지 확인
- 플로이드로 사이클이 존재하는지 확인하는 알고리즘도
심화 개념으로 보인다.