해당 포스팅은 "이것이 취업을 위한 코딩 테스트다 with 파이썬" 책을 기반으로 포스팅하였습니다. ✍️✍️

DFS/BFS

사전 지식

탐색은 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정이다.

이때 대표적인 탐색 알고리즘은 DFS와 BFS이다.

이 DFS와 BFS를 알아보기 위하여 기본 자료구조인 스택과 큐에 대한 개념과 재귀함수, 그래프에 대해서 먼저 알아보자.

스택

스택(Stack)은 상자를 쌓는 것과 비슷하다고 할 수 있다.

일반적으로 상자는 바닥부터 위로 쌓으며, 이를 다시 꺼내기 위해서는 위에서부터 순서대로 꺼낸다.

이러한 구조를 선입후출구조 (First In Last Out) 또는 후입선출구조(Last In First Out)라고 한다.

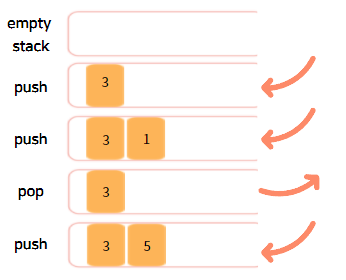
이를 파이썬 코드로 표현하면 다음과 같다.

stack=[]

# 삽입(3) - 삽입(1) - 삭제() - 삽입(5)
stack.append(3)
stack.append(1)
stack.pop()
stack.append(5)

print(stack) # 최하단 원소부터 출력
print(stack[::-1]) # 최상단 원소부터 출력

[3, 5]
[5, 3]

파이썬에서 스택을 이용할 시에는 기본 리스트에 append()와 pop() 메서드를 사용하면 된다.

append()는 리스트의 가장 뒤쪽에 데이터를 삽입하고, pop()은 리스트의 가장 뒤쪽에서 데이터를 꺼내는 함수이다.

큐

큐(Queue)는 대기 줄과 비슷하다고 할 수 있다. 맛집에서 음식을 기다리는 대기줄을 생각해보자. 새치기와 같은 반칙은 없는 기본적인 대기줄의 룰을 생각했을 때, 먼저온 사람이 제일 먼저 먹을 수 있게 된다. 이러한 구조를 선입선출(First In First Out) 구조라고 한다.

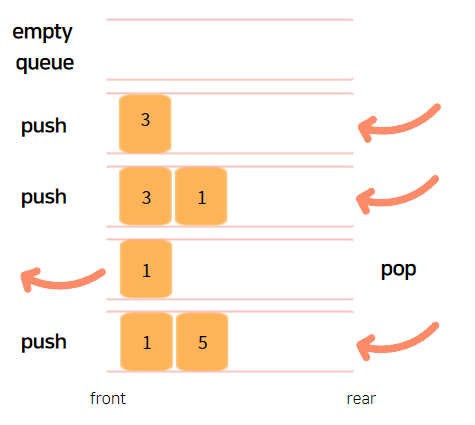
이를 파이썬 코드로 표현하면 다음과 같다.

from collections import deque # 큐 구현을 위해 deque 라이브러리 사용

queue=deque()

# 삽입(3) - 삽입(1) - 삭제() - 삽입(5)
queue.append(3)
queue.append(1)
queue.popleft()
queue.append(5)

print(queue) # 먼저 들어온 원소부터 출력
queue.reverse() # 역순으로 바꾸기
print(queue) # 나중에 들어온 원소부터 출력

deque([1, 5])
deque([5, 1])

파이썬에서 큐를 구현할 시에는 collections 모듈에서 제공하는 deque를 활용한다.

deque는 리스트 자료형에 비해 데이터를 넣고 빼는 것이 효율적이며, queue 라이브러리 보다 간단하다. 또한 대부분의 코딩 테스트에서 collentions 모듈과 같은 기본 라이브러리는 사용하도록 허용하므로 참고하자.

재귀 함수

재귀함수란 자기 자신을 다시 호출하는 함수이다.

예시 코드를 살펴보자.

def func():
    print('hello')
    func()
func()

이 코드를 실행하면 'hello'라는 문자열을 무한히 출력하게 된다. func() 함수는 'hello'를 출력한 후, 다시 자기 자신을 불러오기 때문에 이러한 현상이 발생하게 된다. (참고로 이를 실행했다가 출력을 멈추고 싶으면 ctrl+C를 누르면 무한루프에서 빠져나오게 된다.)

이러한 재귀함수는 특정 조건을 만족할 시 반복적인 코드가 종료되거나, 함수가 진행됨에 따라 수렴하는 식으로 종료가 되는 형태로 코드를 작성할 때 자주 사용된다.

이러한 재귀함수를 사용시, 반복문을 사용하는 것보다 더 간결하게 표현할 수 있는 경우들이 있으니, 이점을 참고해서 코드를 작성하면 좋을 것 같다.

그래프

그래프는 노드(Node)와 간선(Edge)으로 이루어져있다. 이때 노드를 정점(Vertex)이라고도 말한다.

두 노드가 간선으로 연결되어 있는 것을 '두 노드가 인접하다'라고 한다.

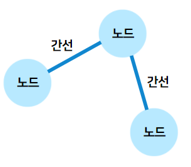
이러한 그래프를 표현하는 방식으로는 인접 행렬과 인접 리스트가 있다.

• 인접 행렬: 2차원 배열로 그래프의 연결 관계를 표현
• 인접 리스트: 리스트로 그래프의 연결 관계를 표현

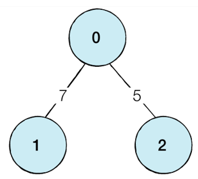
위 그래프에 대한 인접 행렬은 다음과 같다.

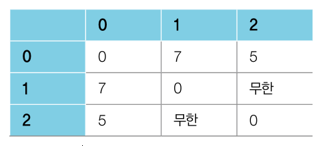
위 인접행렬을 파이썬으로 작성해보자.

(이때 연결이 되어있지 않은 코드는 무한의 비용으로 작성한다.)

# 인접 행렬 예제
INF = 999999999 # 무한의 비용 선언

graph = [
    [0, 7, 5],
    [7, 0, INF],
    [5, INF, 0]
]

print(graph)

[[0, 7, 5], [7, 0, 999999999], [5, 999999999, 0]]

위 그래프에 대한 인접 리스트는 다음과 같이 생성할 수 있다.

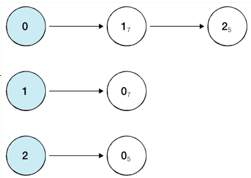
인접 리스트는 위 그림과 같이, 모든 노드에 대해 연결된 다른 노드의 정보만을 연결하여 저장한다.

이를 파이썬 코드로 작성하면 다음과 같다.

# 인접 리스트 예제
graph = [[] for _ in range(3)] # 총 노드가 3개인 그래프에 대한 인접 리스트

# 노드 0에 연결된 다른 노드들의 정보 (노드, 거리)
graph[0].append((1, 7))
graph[0].append((2, 5))

# 노드 1에 연결된 다른 노드들의 정보 (노드, 거리)
graph[1].append((0, 7))

# 노드 2에 연결된 다른 노드들의 정보 (노드, 거리)
graph[2].append((0, 5))

print(graph)

[[(1 ,7), (2, 5)], [(0, 7)], [(0, 5)]]

인접 행렬은 인접 리스트보다 직관적이지만, 대용량 데이터에 사용하기에는 메모리상 비효율적이라는 단점이 있다. 반면, 인접 리스트는 연결된 정보만을 저장하기 때문에 효율적으로 메모리를 사용할 수 있다.

DFS

DFS(Depth-First Search)는 깊이 우선 탐색이라고도 불린다.

(이때 그래프를 탐색한다는 것은 하나의 노드를 시작으로 모든 노드들을 한번씩 방문하는 것을 말한다.)

이 DFS 현재 노드의 자식의 자식들을 처리해 준다고 할 수 있다. 즉, 현재 노드의 자식, 그 자식 노드의 자식, 그 자식 노드의 자식 .. 으로 제일 말단 노드까지 찍고 그 다음 다시 올라와 다른 자식에 대한 자식의 자식의 ... 이런 식으로 처리하기 때문에 깊이 우선 탐색이라고 하는 것이다.

DFS는 깊이 부분에서 얕은 것부터 깊은 것 순으로 우선 처리한 후, 그 다음 너비 부분에서 얕고 깊은 것들을 고려한다. (이때, 제일 깊은 노드를 방문한 후, 다시 그 다음으로 얕은 다른 노드를 갈 때에는 방문을 생략하고 이동한다.)

DFS는 스택 자료구조를 사용하며, 구체적인 동작과정은 다음과 같다.

1. 탐색 시작 노드를 스택에 삽입 후, 방문 처리를 한다.
2. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 있을 시, 그 노드를 스택에 삽입 후, 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면, 다시 스택에서 최상단 노드(가장 얕은 노드)를 꺼낸다.
3. 2번을 더 이상 수행할 노드가 없을 때까지 반복한다.

이때 방문 처리는 스택에 한 번 삽입 되었던 노드가 다시 삽입되지 않도록 처리하는 것이다. 따라서 각 노드는 한번씩만 방문 처리를 하게 된다.

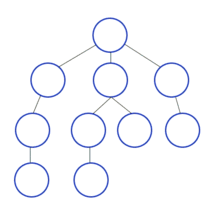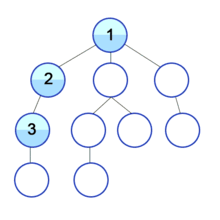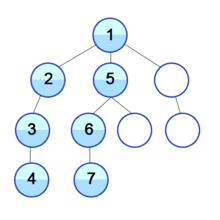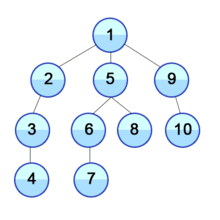
이미지 출처: https://ko.wikipedia.org

이를 파이썬으로 다음과 같이 구현할 수 있다.

def dfs(graph, v, visited):
    visited[v] = True # 현재 노드를 방문 처리
    print(v, end=' ')
    for i in graph[v]:
        if not visited[i]:
            dfs(graph, i, visited) # 현재 노드와 연결된 다른 노드를 재귀적으로 방문

# 각 노드가 연결된 정보를 리스트 자료형으로 표현 (2차원)
graph = [
    [],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]

# 각 노드가 방문된 정보를 리스트 자료형으로 표현 (1차원)
visited = [False]*9

# 정의된 DFS 함수 호출
dfs(graph, 1, visited)

1 2 7 6 8 3 4 5

BFS

BFS(Breadth First Search) 알고리즘은 너비 우선 탐색이라고도 한다.

현재 노드와 연결된 자식들을 먼저 처리한다고 할 수 있다. 즉, 현재 노드의 모든 자식 노드를 처리한 다음, 그 중 한 노드의 모든 자식 노드를 처리하고 ... 이런식으로 같은 깊이에 해당되는 노드들을 처리하면서 깊어지기 때문에 너비 우선 탐색이라고 하는 것이다.

BFS는 너비 부분에서 얕은 것부터 깊은 것 순으로 우선 처리한 후, 그 다음 깊이 부분에서 얕고 깊은 것들을 고려한다.

BFS는 큐 자료구조를 사용하며, 구체적인 동작과정은 다음과 같다.

1. 탐색 시작 노드를 스택에 삽입 후, 방문 처리를 한다.
2. 큐에서 노드를 꺼내, 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
3. 2번을 더 이상 수행할 노드가 없을 때까지 반복한다.

이때 방문 처리는 스택에 한 번 삽입 되었던 노드가 다시 삽입되지 않도록 처리하는 것이다. 따라서 각 노드는 한번씩만 방문 처리를 하게 된다.

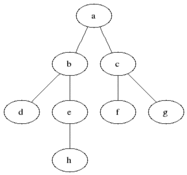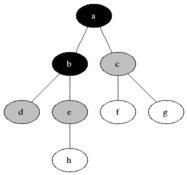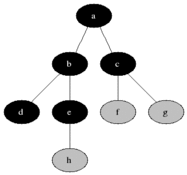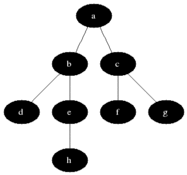
이미지 출처: https://ko.wikipedia.org

이를 파이썬으로 다음과 같이 구현할 수 있다.

from collections import deque

def bfs(graph, start, visited):
    queue = deque([start])
    visited[start] = True # 현재 노드를 방문 처리
    while queue:
        # 큐에서 하나의 원소를 뽑아 출력
        v = queue.popleft()
        print(v, end=' ')
        # 해당 원소와 인접한, 아직 방문하지 않은 원소들을 큐에 삽입
        for i in graph[v]:
            if not visited[i]:
                queue.append(i)
                visited[i] = True

# 각 노드가 연결된 정보를 리스트 자료형으로 표현 (2차원)
graph = [
    [],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]

# 각 노드가 방문된 정보를 리스트 자료형으로 표현 (1차원)
visited = [False]*9

# 정의된 BFS 함수 호출
bfs(graph, 1, visited)

1 2 3 8 7 4 5 6

그러면 코딩 테스트 문제에서 어떤 경우에 이 탐색 알고리즘을 사용할 수 있을까?

1차원 배열이나 2차원 배열을 그래프 형태로 생각하여 DFS와 BFS를 사용하는 풀이방법을 생각해 볼 수 있다.

실전 문제 1

난이도 중 | 풀이 시간 30분 | 시간 제한 1초 | 메모리제한 128MB

N × M 크기의 얼음 틀이 있다. 구멍이 뚫려 있는 부분은 0, 칸막이가 존재하는 부분은 1로 표시된다. 구멍이 뚫려 있는 부분끼리 상, 하, 좌, 우로 붙어 있는 경우 서로 연결되어 있는 것으로 간주한다. 이때 얼음 틀의 모양이 주어졌을 때 생성되는 총 아이스크림의 개수를 구하는 프로그램을 작성하라. 다음의 4 × 5 얼음 틀 예시에서는 아이스크림이 총 3개가 생성된다.

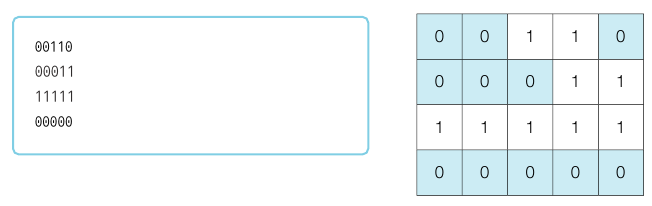
입력 조건

• 첫 번째 줄에 얼음 틀의 세로 길이 N과 가로 길이 M이 주어진다. (1 <= N, M <= 1,000)
• 두 번째 줄부터 N + 1 번째 줄까지 얼음 틀의 형태가 주어진다.
• 이때 구멍이 뚫려있는 부분은 0, 그렇지 않은 부분은 1이다.

출력 조건

• 한 번에 만들 수 있는 아이스크림의 개수를 출력한다.

입력 예시

15 14
00000111100000
11111101111110
11011101101110
11011101100000
11011111111111
11011111111100
11000000011111
01111111111111
00000000011111
01111111111000
00011111111000
00000001111000
11111111110011
11100011111111
11100011111111

출력 예시

8

이 문제는 DFS로 해결할 수 있다.

실전 문제 2

난이도 중 | 풀이 시간 30분 | 시간 제한 1초 | 메모리제한 128MB

N x M 크기의 직사각형 형태의 미로에 여러 마리의 괴물이 있어 이를 피해 탈출해야 한다. 현재 위치는 (1, 1)이고 미로의 출구는 (N,M)의 위치에 존재하며 한 번에 한 칸씩 이동할 수 있다. 괴물이 있는 부분은 0으로, 괴물이 없는 부분은 1로 표시되어 있다. 미로는 반드시 탈출할 수 있는 형태로 제시된다. 이때 탈출하기 위해 움직여야 하는 최소 칸의 개수를 구하라. 칸을 셀 때는 시작 칸과 마지막 칸을 모두 포함해서 계산한다.

입력 조건

• 첫째 줄에 두 정수 N, M(4 <= N, M <= 200)이 주어진다. 다음 N개의 줄에는 각각 M개의 정수(0 혹은 1)로 미로의 정보가 주어진다. 각각의 수들은 공백 없이붙어서 입력으로 제시된다. 또한 시작 칸과 마지막 칸은 항상 1이다.

출력 조건

• 첫째 줄에 최소 이동 칸의 개수를 출력한다.

입력 예시

5 6
101010
111111
000001
111111
111111

출력 예시

10

이 문제는 BFS로 해결할 수 있다.

---

본 책 저자의 깃허브에 이미 책에 실린 문제들에 대한 풀이 코드들이 정리된 repository가 있으니 위 문제에 대한 답을 참고하고 싶으신 분은 github.com/ndb796/python-for-coding-test를 통해 참고해주시기 바랍니다!