PyTorch에서 autograd 동작 이해하기

Cammie·2022년 10월 17일

Computational Graph PyTorch autograd backward zero_grad()

PyTorch

목록 보기

4/4

Autograd

Autograd ; Automatic gradient calculating API
forward와 backward가 가능하게 해줌
즉, 해당 변수가 계산되는 데에 사용했던 모든 변수들의 미분값을 구하면서 forward 또는 backward를 진행하게 해준다.
해당 변수가 계산되어 온 history를 Computational Graph로 가지고 있어서 이러한 동작이 가능한 것이다.

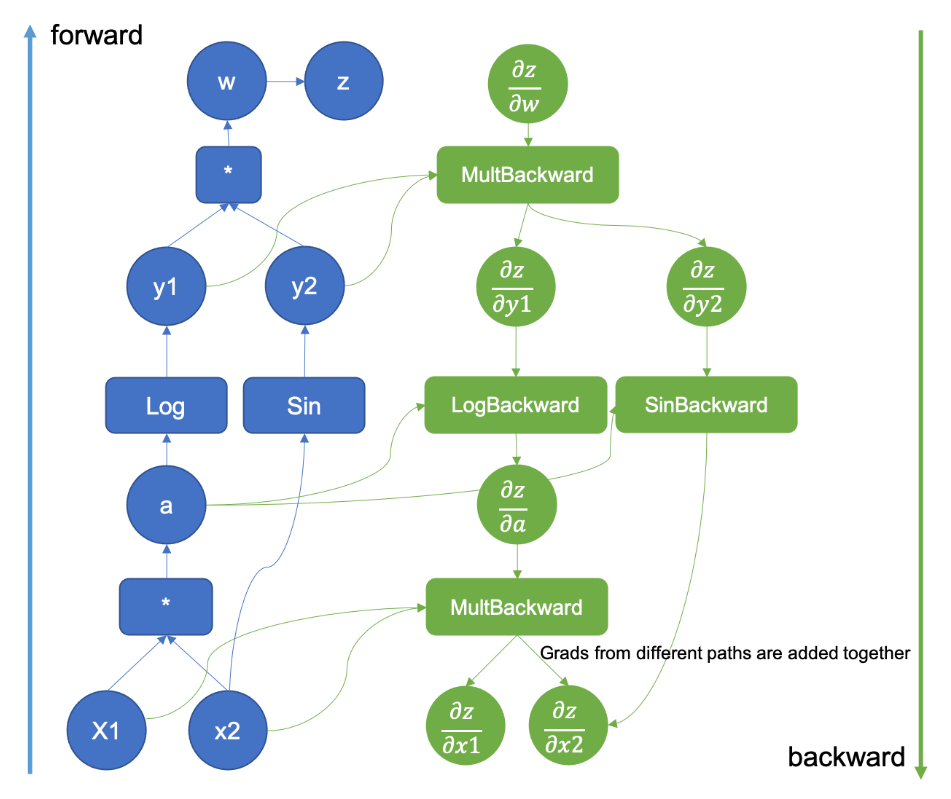
위 이미지와 같은 Computational Graph를 사용하여 Autograd가 진행된다.

autograd를 사용한 예제를 살펴보자.

x = torch.ones(2,2, requires_grad=True) # requires_grad=True로 해야 x의 연산들을 추적하기 시작한다.

'''
print(x) 는 다음과 같음
tensor([[1., 1.],
        [1., 1.]], requires_grad=True)
'''

y = x+1

'''
print(y) 는 다음과 같음
tensor([[2., 2.],
        [2., 2.]], grad_fn=<AddBackward0>)
'''

z = 2*y**2
res = z.mean()

'''
print(res) 는 다음과 같음
tensor(8., grad_fn=<MeanBackward0>)
'''

res.backward() # 역전파 계산

'''
print(x.grad) 는 다음과 같음 (계산한 x의 미분값 출력)
tensor([[2., 2.],
        [2., 2.]])
'''

위 코드의 계산 과정을 수식으로 보면 다음과 같다.

res = z.mean() 이었으므로 $res = \dfrac{(z_1 + .. + z_4)}{4}$ 이다.
이때 $z_i = 2 * y_i^2$ 이다.
$y_i = x_i+1$ 이었으므로, $z_i = 2(x_i+1)^2$ 이다.
$\dfrac{d(res)}{dx_i}$ 는 1번 전개에 의해 $\dfrac{d(z)}{4\cdot dx_i}$ 이다.
이때 $\dfrac{d(z)}{dx_i} = 4(x_i+1)$ 이다.
따라서 $\dfrac{d(res)}{dx_i}$ 는 $x_i+1$ 이다.
처음에 x = torch.ones(2,2, requires_grad=True) 이었으므로, x는 1로 채워진 2 x 2 행렬이다.
따라서 x.grad는 여기에 1씩 더한 tensor([[2., 2.], [2., 2.]])가 된다.

보다시피 단순한 연산 몇 개에 대한 계산임에도 꽤나 복잡하다..
이러한 연산을 직관적이고 간단히 해주는 pytorch에게 박수를 👏👏

☠️ autograd 사용 시 주의해야 할 점 ☠️

순전파/역전파를 적용할 변수를 선언할 때 requires_grad=True 로 해야 x의 연산들을 추적하기 시작한다.
backward를 두 번 호출하게 되면 에러가 뜬다.
backward를 한 번 호출하면, 이를 계산한 computational graph를 그대로 가지고 있으면 메모리적으로 비효율적이므로 이를 날려버리는 것이 default이다. 따라서, backward를 두 번 호출하게 되면 에러가 뜨며, 만약 또 호출하고 싶으면 처음 backward 시에 retain_graph=True 옵션을 지정해 주어야 한다. (이렇게 하게되면 두번째에서부터 이전 gradient 결과값에 누적되어 더해지는 식으로 계산이 된다.)
retain_graph=True를 안하더라도 zero_grad()를 해주지 않으면, gradient 결과값들이 계속 누적이 된다.

🧐Computational Graph를 통한 autograd 동작 원리

위에서 변수가 계산되어 온 history를 Computational Graph형태로 가지고 있다고 했었다.

이때 각 변수의 미분연산을 grad_fn (gradient function) 이라는 클래스 객체로서 각각의 연산이 무엇인지 Computational Graph에 저장된다. (e.g. grad_fn=<AddBackward0>)

즉,
① .backward를 하면 역전파가 시작되고,
② 해당 변수의 미분연산 .grad_fn 클래스가 호출이 되면서 미분값들이 계산되며,
③ 이 값이 .grad에 누적되면서 모든 노드에 대한 역전파가 일어나게 되는 것이다.

실제 딥러닝 훈련에서 사용되는 autograd

import torch
import torch.nn as nn
import torch.optim as optim

BATCH_SIZE = 256
train_iter = torch.utils.data.DataLoader(mnist_train,batch_size=BATCH_SIZE,shuffle=True)

loss = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(),lr=1e-3) # 이때 model은 사용자가 정의한 딥러닝 모델

for epoch in range(EPOCHS):
    total_loss = 0
    for batch_in,batch_out in train_iter:
        y_pred = model.forward(batch_in.view(-1,1,28,28).to(device))
        loss_out = loss(y_pred,batch_out.to(device))
        # Update
        optimizer.zero_grad()   # reset gradient 
        loss_out.backward() 	# loss_out을 계산하는 것에 관여한 노드들에 대해 backpropagate
        optimizer.step()        # 파라미터 값들이 현재의 gradient값에 기반하여 업데이트 되도록 수행
        total_loss += loss_out

Cammie

이전 포스트